Full Report for Apart by Kanare Kato

Apart is a game in which the goal is to distribute your pieces, as opposed to a game in which you create groups.

Rules

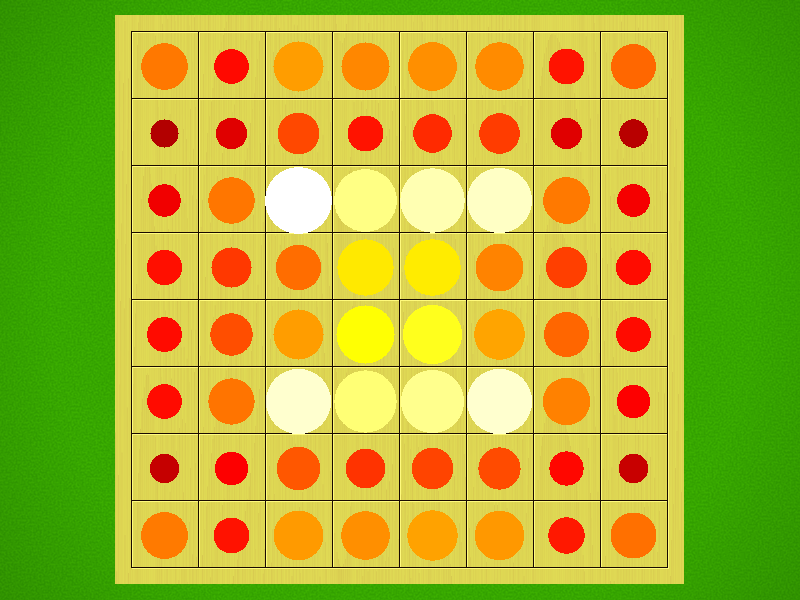
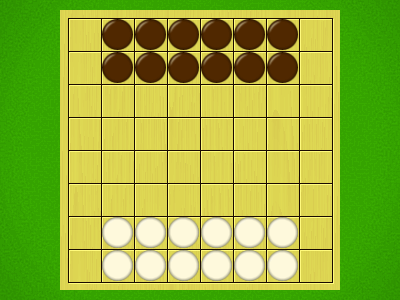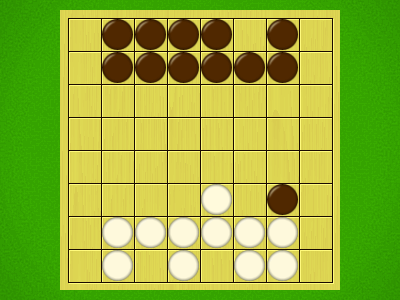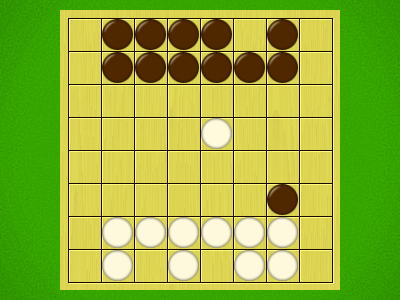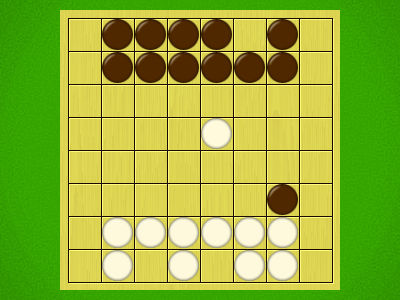
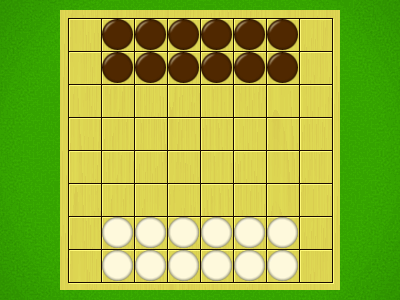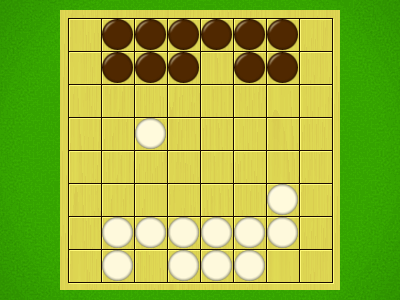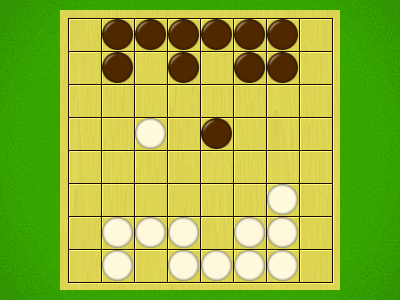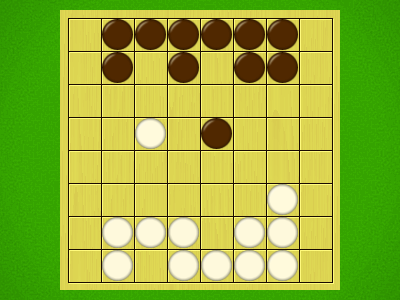
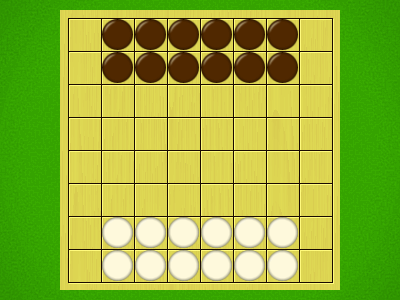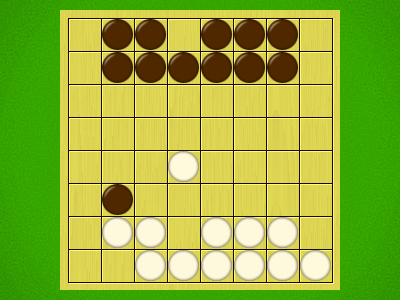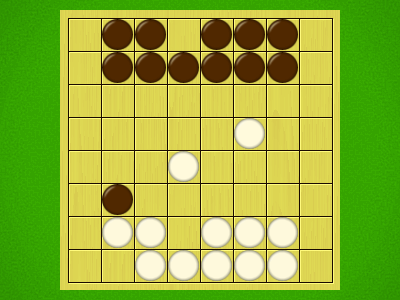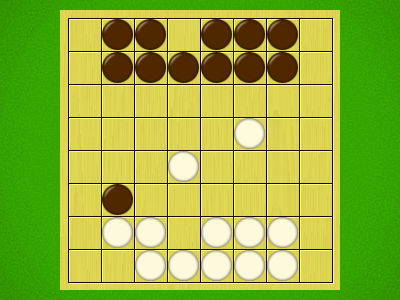
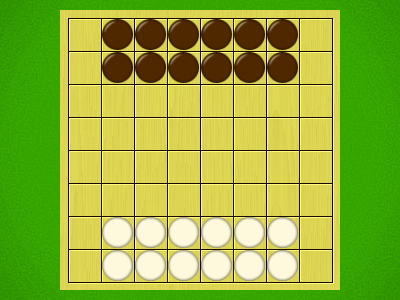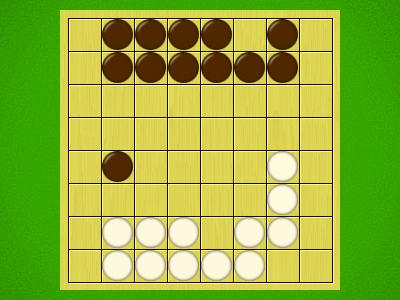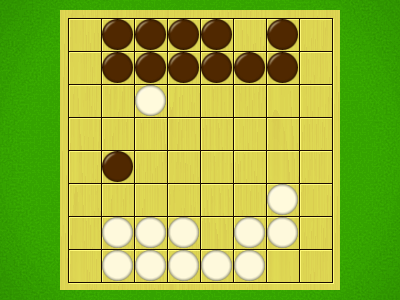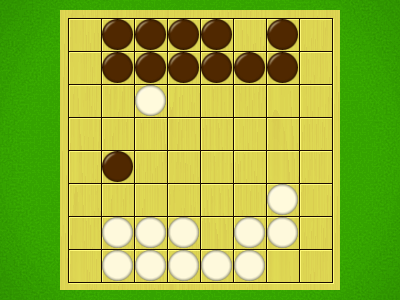
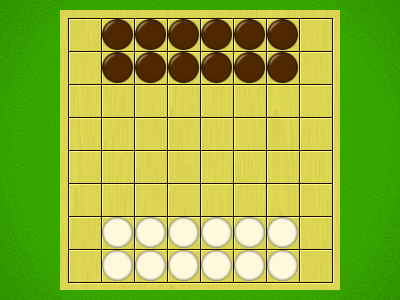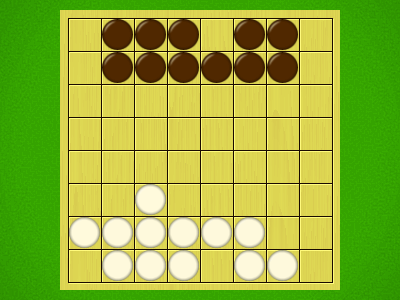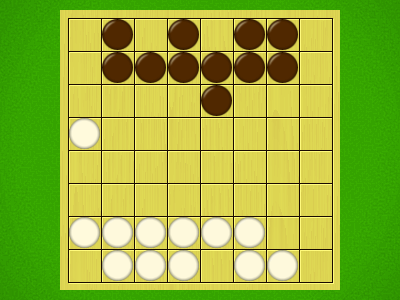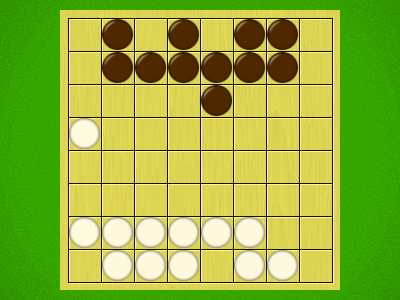
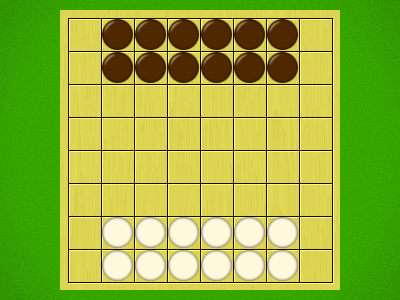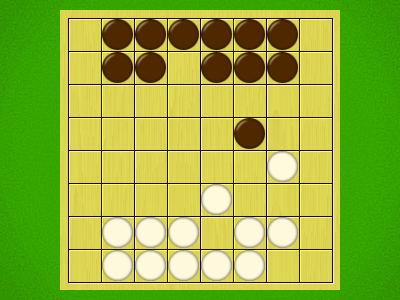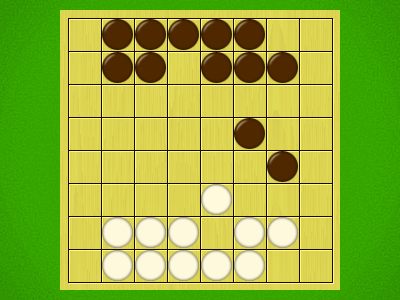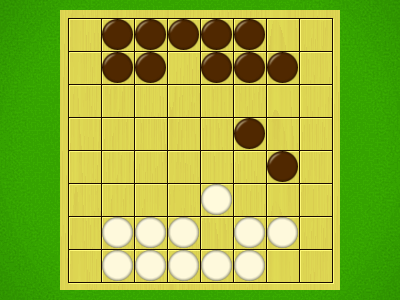
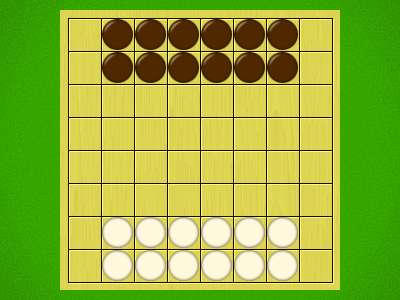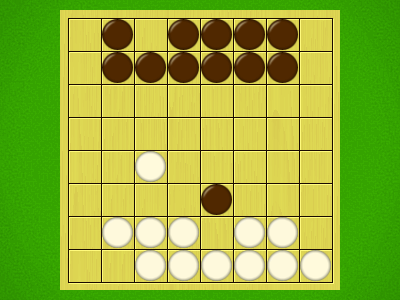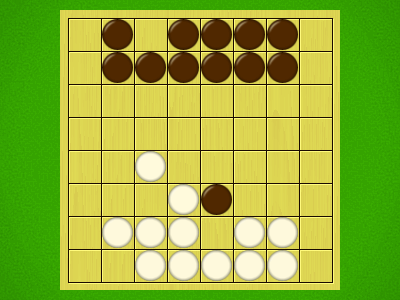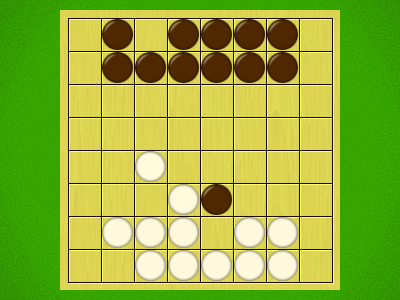
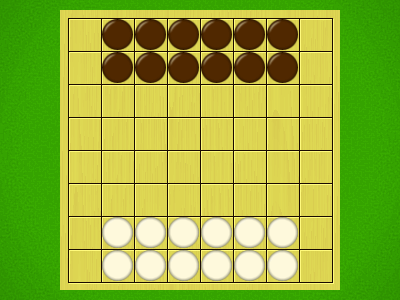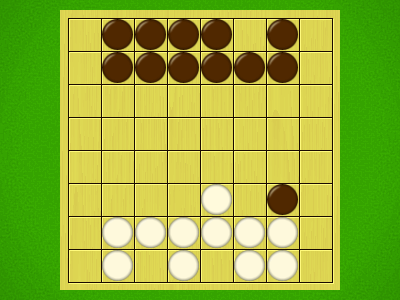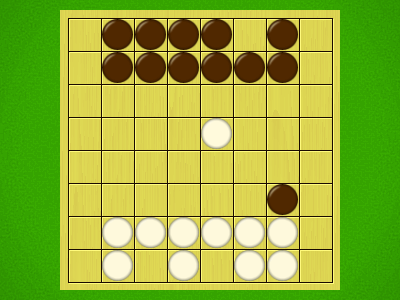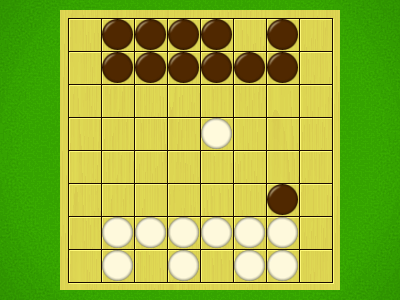
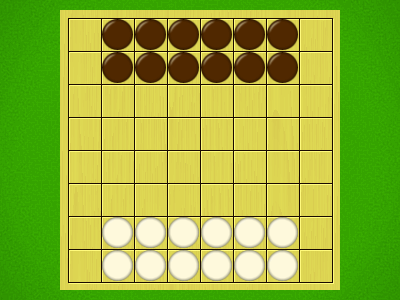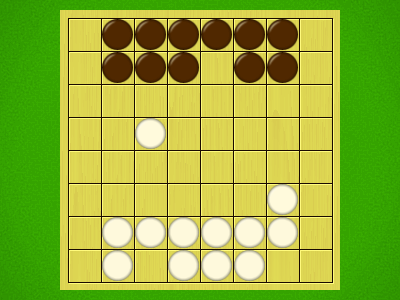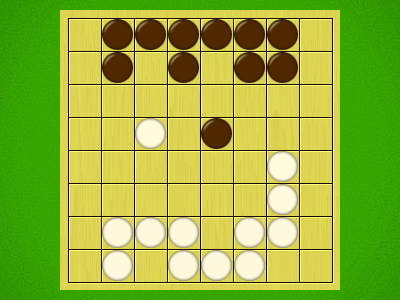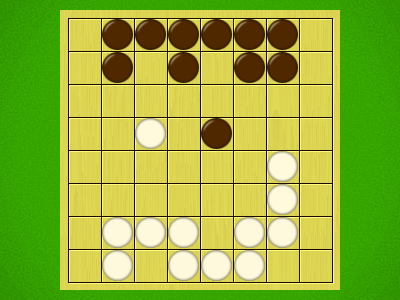
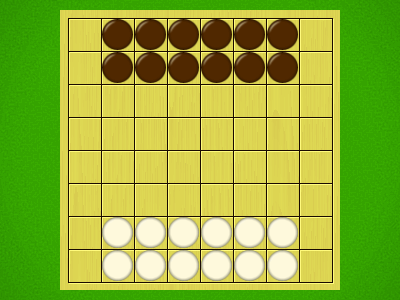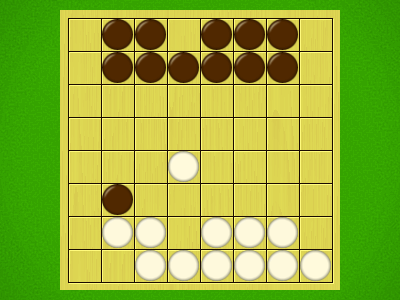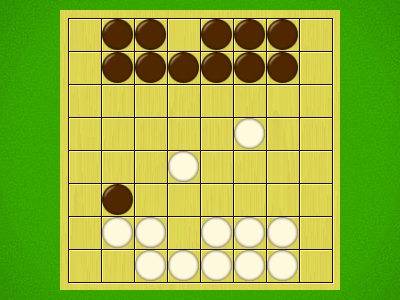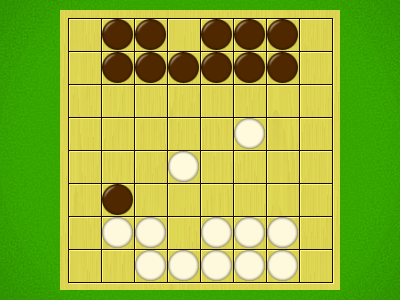
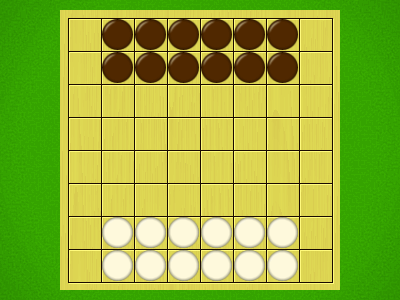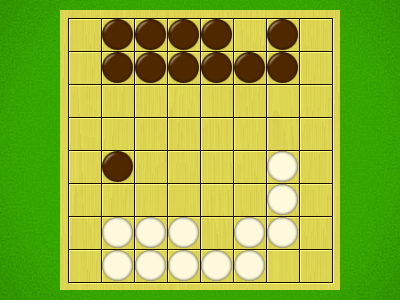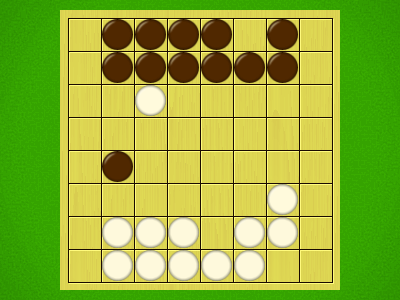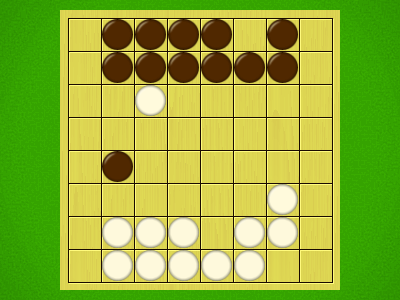
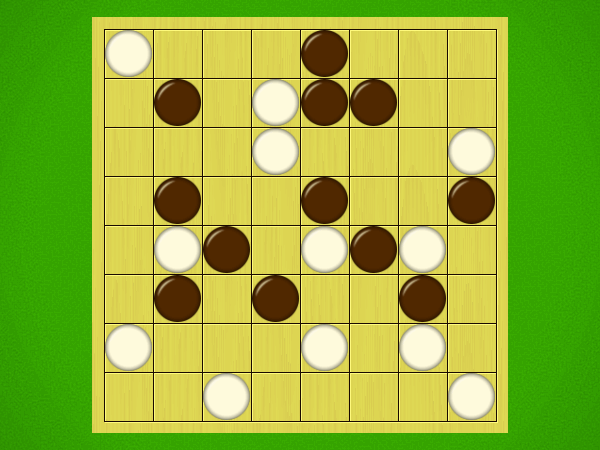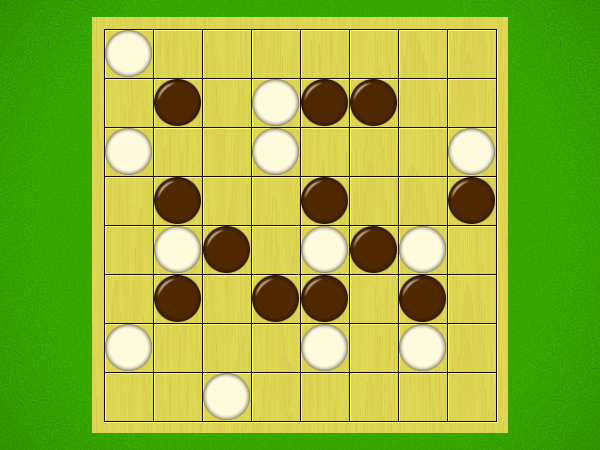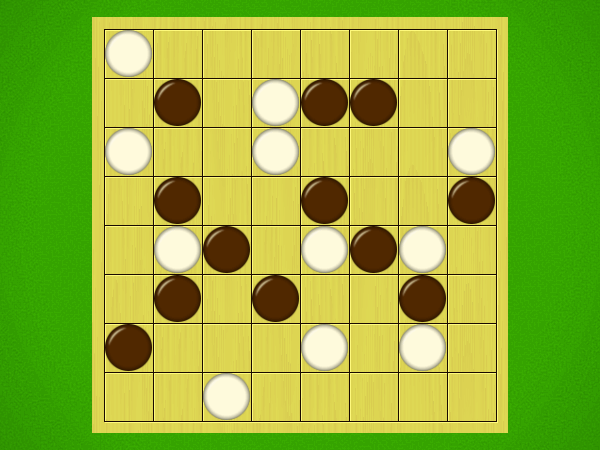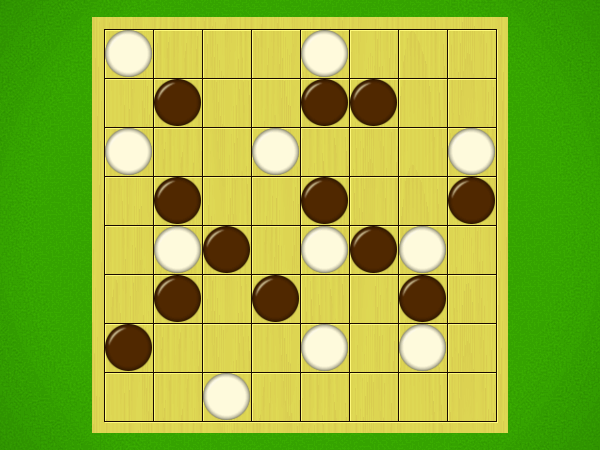
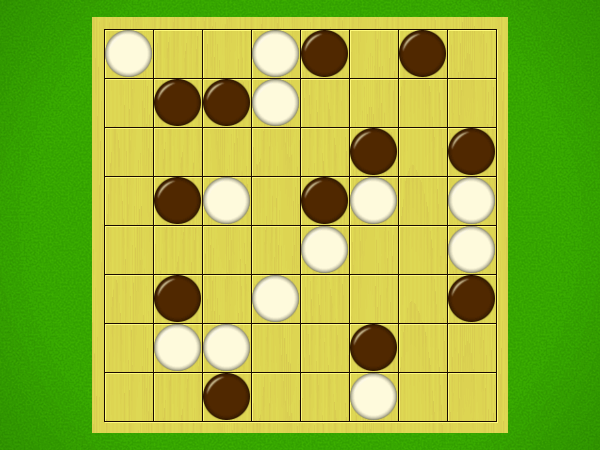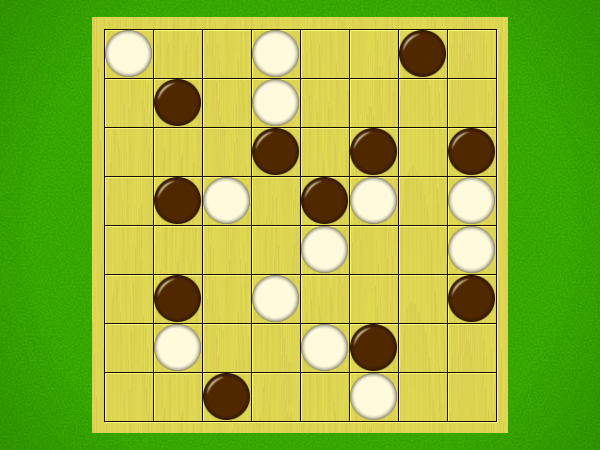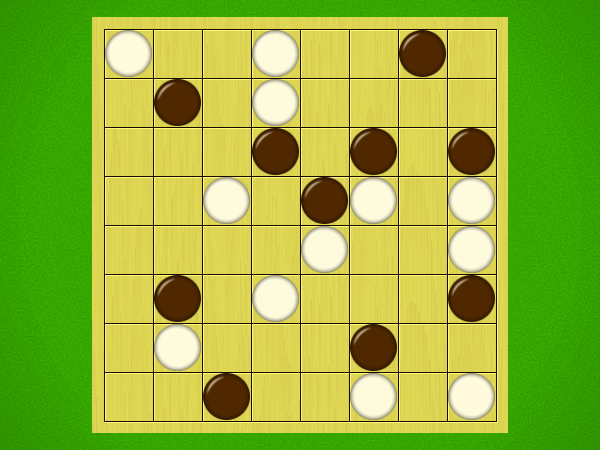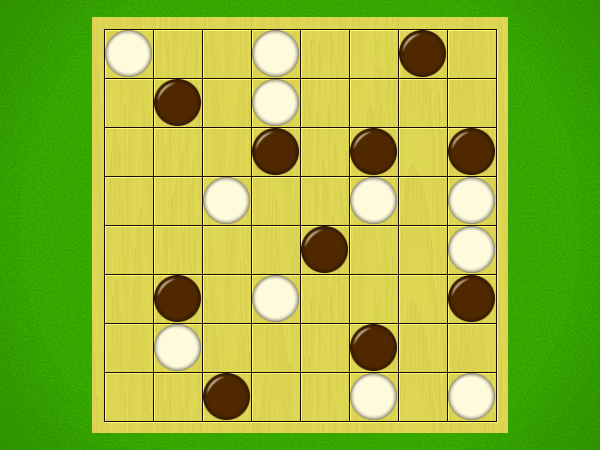
Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!

Definitions

Line: Same-colour pieces arranged in an unbroken straight line are called a line. The length of a line is the number of pieces belonging to that line. A row with only one piece in it is considered a line of length 1. Therefore, each piece belongs to multiple lines at any time.
Step: Moving a piece to an adjacent space is called a step.
Jump: Moving a piece two or more squares is called a jump.

Play

White plays first, then turns alternate; on White's first move, jumping more than once is not allowed.

Pieces move in straight lines, a distance exactly equal to the length of the line in that direction.

An enemy piece in the destination space is captured

If the move is a Jump (more than one space) then:

Pieces in jumped spaces are ignored
You cannot capture or land on a friendly piece
You may continue to Jump with the same piece, but may not visit the same space twice

Game End

Play continues until a player separates all their pieces. They win.

Miscellaneous

General comments:

Requires αβ search to play well.

Play: Combinatorial

Family: Combinatorial 2023

Mechanism(s): Movement,Capture

Components: Board

Level: Advanced

BGG Stats

BGG Entry	Apart
BGG Rating	null
#Voters	null
SD	null
BGG Weight	null
#Voters	null
Year	null

Kolomogorov Complexity Analysis

Size (bytes)	27309
Reference Size	10915
Ratio	2.50

Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.

Playout Complexity Estimate

Playouts per second	12666.38 (78.95µs/playout)
Reference Size	411514.67 (2.43µs/playout)
Ratio (low is good)	32.49

Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.

State Space Complexity

% new positions/bucket

Samples	1402834
Confidence	0.00	0: totally unreliable, 100: perfect

State space complexity (where present) is an estimate of the number of distinct game tree reachable through actual play. Over a series of random games, Ai Ai checks each position to see if it is new, or a repeat of a previous position and keeps a total for each game. As the number of games increase, the quantity of new positions seen per game decreases. These games are then partitioned into a number of buckets, and if certain conditions are met, Ai Ai treats the number in each bucket as the start of a strictly decreasing geometric sequence and sums it to estimate the total state space. The accuracy is calculated as 1-[end bucket count]/[starting bucklet count]

Playout/Search Speed

Label	Its/s	SD	Nodes/s	SD	Game length	SD
Random playout	13,562	49	1,985,558	6,186	146	40
search.UCT	14,035	450			118	31
search.AlphaBeta	196,845	37,495			70	8

Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.

Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.

Mirroring Strategies

Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.

Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.

Heuristic Values

This chart shows the heuristic values thoughout a single representative* game. The orange line shows the difference between player scores. (* Representative, in the sense that it is close to the mean game length.)

Win % By Player (Bias)

1: White win %	53.70±3.10	Includes draws = 50%
2: Black win %	46.30±3.07	Includes draws = 50%
Draw %	0.00	Percentage of games where all players draw.
Decisive %	100.00	Percentage of games with a single winner.
Samples	1000	Quantity of logged games played

Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)

Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.

UCT Skill Chains

Match	AI	Strong Wins	Draws	Strong Losses	#Games	Strong Score	p1 Win%	Draw%	p2 Win%	Game Length
0	Random
1	UCT (its=2)	631	0	369	1000	0.6006 <= 0.6310 <= 0.6604	48.50	0.00	51.50	147.37
6	UCT (its=7)	631	0	330	961	0.6260 <= 0.6566 <= 0.6860	49.32	0.00	50.68	147.46
40	UCT (its=109)	631	0	71	702	0.8743 <= 0.8989 <= 0.9190	51.28	0.00	48.72	144.78
41	UCT (its=296)	185	0	35	220	0.7868 <= 0.8409 <= 0.8833	49.55	0.00	50.45	141.75
42	UCT (its=296)	495	0	505	1000	0.4641 <= 0.4950 <= 0.5259	48.50	0.00	51.50	144.03

Search for levels ended: time limit reached.

Level of Play: Strong beats Weak 60% of the time (lower bound with 95% confidence).

Draw%, p1 win% and game length may give some indication of trends as AI strength increases.

1st Player Win Ratios by Playing Strength

This chart shows the win(green)/draw(black)/loss(red) percentages, as UCT play strength increases. Note that for most games, the top playing strength show here will be distinctly below human standard.

Complexity

Game length	77.72
Branching factor	15.66
Complexity	10^53.00	Based on game length and branching factor
Samples	1000	Quantity of logged games played

Computational complexity (where present) is an estimate of the game tree reachable through actual play. For each game in turn, Ai Ai marks the positions reached in a hashtable, then counts the number of new moves added to the table. Once all moves are applied, it treats this sequence as a geometric progression and calculates the sum as n-> infinity.

Move Classification

Board Size	64	Quantity of distinct board cells
Distinct actions	1176	Quantity of distinct moves (e.g. "e4") regardless of position in game tree
Killer moves	173	A 'killer' move is selected by the AI more than 50% of the time Too many killers to list.
Good moves	590	A good move is selected by the AI more than the average
Bad moves	586	A bad move is selected by the AI less than the average
Terrible moves	161	A terrible move is never selected by the AI Too many terrible moves to list.
Response distance%	32.44%	Distance from move to response / maximum board distance; a low value suggests a game is tactical rather than strategic.
Samples	1000	Quantity of logged games played

Board Coverage

A mean of 72.17% of board locations were used per game.

Colour and size show the frequency of visits.

Game Length

Game length frequencies.

Mean	77.72
Mode	[77]
Median	77.0

Change in Material Per Turn

Mean change in material/round	-0.39	Complete round of play (all players)

This chart is based on a single representative* playout, and gives a feel for the change in material over the course of a game. (* Representative in the sense that it is close to the mean length.)

Actions/turn

Table: branching factor per turn, based on a single representative* game. (* Representative in the sense that it is close to the mean game length.)

Action Types per Turn

This chart is based on a single representative* game, and gives a feel for the types of moves available throughout that game. (* Representative in the sense that it is close to the mean game length.)

Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.

Trajectory

This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).

The lead changed on 2% of the game turns. Ai Ai found 8 critical turns (turns with only one good option).

Position Heatmap

This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).

Good/Effective moves

Measure	All players	Player 1	Player 2
Mean % of effective moves	95.76	92.98	98.69
Mean no. of effective moves	11.36	11.40	11.32
Effective game space	10^49.42	10^24.84	10^24.57
Mean % of good moves	17.52	23.82	10.90
Mean no. of good moves	1.65	2.00	1.29
Good move game space	10^9.89	10^7.43	10^2.46

These figures were calculated over a single game.

An effective move is one with score 0.1 of the best move (including the best move). -1 (loss) <= score <= 1 (win)

A good move has a score > 0. Note that when there are no good moves, an multiplier of 1 is used for the game space calculation.

Quality Measures

Measure	Value	Description
Hot turns	19.23%	A hot turn is one where making a move is better than doing nothing.
Momentum	2.56%	% of turns where a player improved their score.
Correction	19.23%	% of turns where the score headed back towards equality.
Depth	1.18%	Difference in evaluation between a short and long search.
Drama	0.20%	How much the winner was behind before their final victory.
Foulup Factor	20.51%	Moves that looked better than the best move after a short search.
Surprising turns	1.28%	Turns that looked bad after a short search, but good after a long one.
Last lead change	5.13%	Distance through game when the lead changed for the last time.
Decisiveness	6.41%	Distance from the result being known to the end of the game.

These figures were calculated over a single representative* game, and based on the measures of quality described in "Automatic Generation and Evaluation of Recombination Games" (Cameron Browne, 2007). (* Representative, in the sense that it is close to the mean game length.)

Openings

Moves	Animation
e1-g3,f8-d6,d6-g3,Pass,c1-e3,e3-e1,e1-a1,a1-c3,c3-e5,Pass
g1-g3,e7-c5,Pass,c1-c3,c3-c5,Pass,c7-e5,Pass,e2-g4,g4-g1
d2-d4,d8-b6,b6-b3,Pass,b1-h1,h1-f3,f3-d5,d5-d3,d3-f5,Pass
g1-g3,f8-d6,d6-b4,Pass,e2-g4,g4-g1,g1-a1,a1-c3,c3-c6,Pass
g2-a2,e8-c6,c6-c3,Pass,e1-c3,c3-a1,a1-a3,a3-a5,Pass,c8-e6
g1-e3,d7-f5,Pass,e2-g4,Pass,g8-a8,a8-c6,c6-e4,e4-g6,g6-g4
e2-c4,c8-e6,e6-e3,Pass,b1-h1,h1-f3,f3-d5,d5-b3,b3-b5,b5-d3
e2-c4,c8-c6,c6-c4,Pass,c2-c4,Pass,e8-a8,a8-c6,c6-c4,Pass
e1-g3,f8-d6,d6-g3,Pass,c1-e3,e3-e1,e1-a1,a1-c3,c3-e5
g1-g3,e7-c5,Pass,c1-c3,c3-c5,Pass,c7-e5,Pass,e2-g4
d2-d4,d8-b6,b6-b3,Pass,b1-h1,h1-f3,f3-d5,d5-d3,d3-f5
g1-g3,f8-d6,d6-b4,Pass,e2-g4,g4-g1,g1-a1,a1-c3,c3-c6

Opening Heatmap

Colour shows the success ratio of this play over the first 10moves; black < red < yellow < white.

Size shows the frequency this move is played.

Unique Positions Reachable at Depth

0	1	2	3	4	5	6	7
1	40	1640	13972	141038	590483	2422010	8520504

Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.

Puzzle	Solution
White to win in 13 moves
Black to win in 12 moves
White to win in 11 moves
White to win in 12 moves