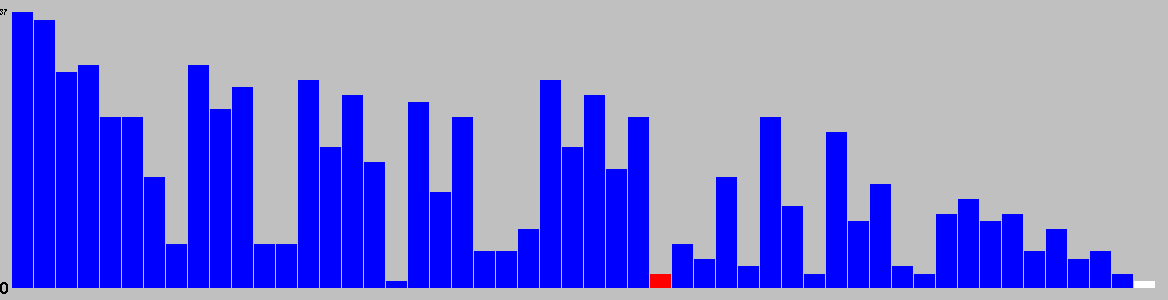
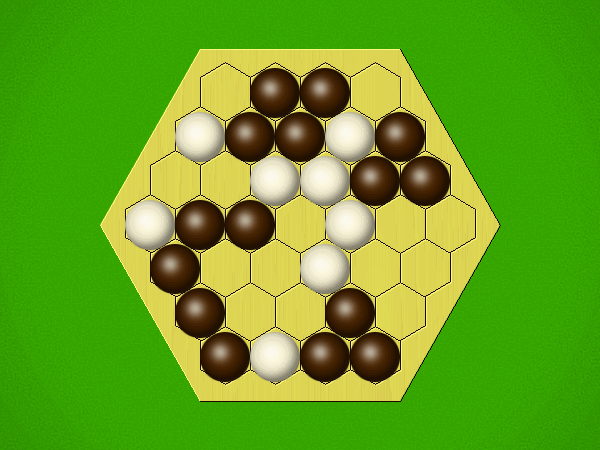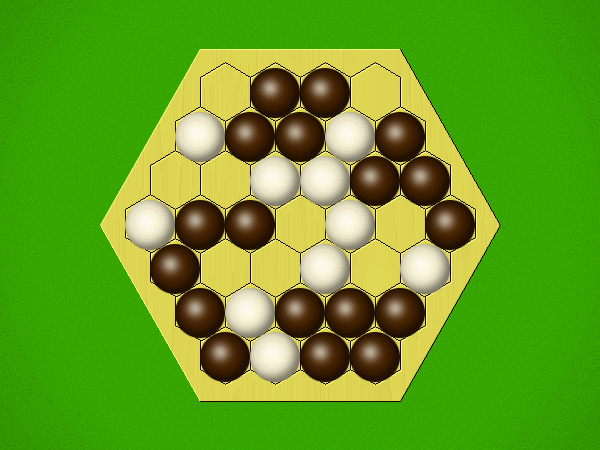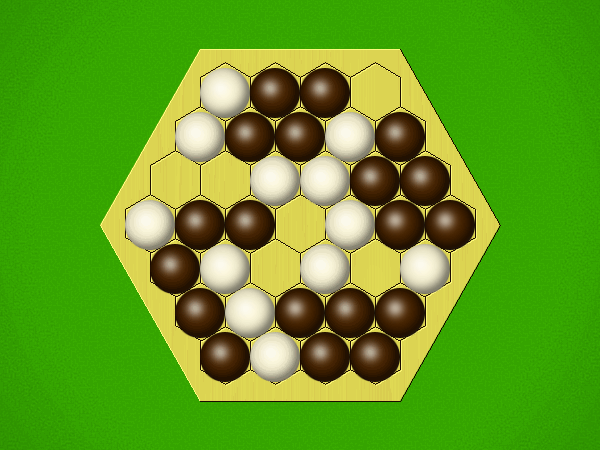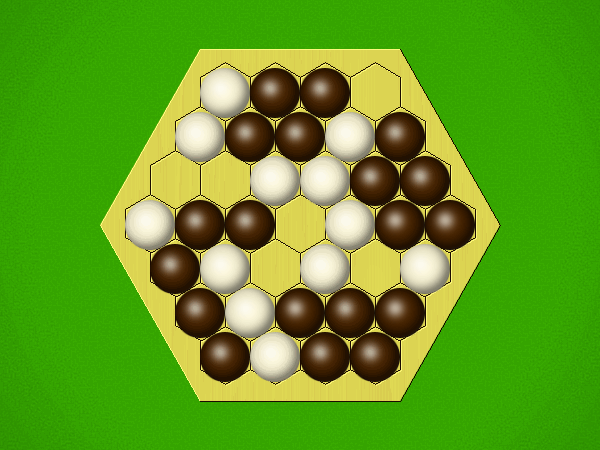
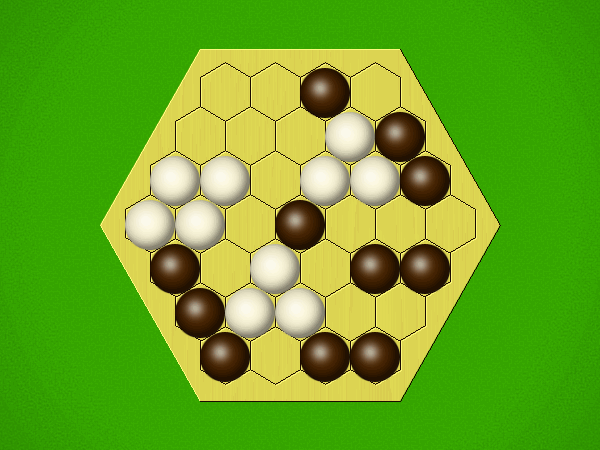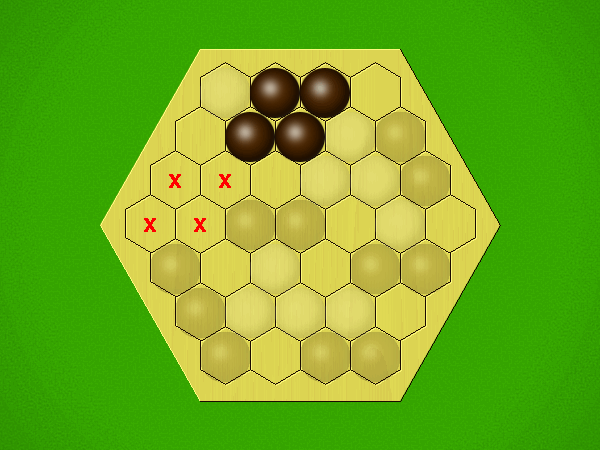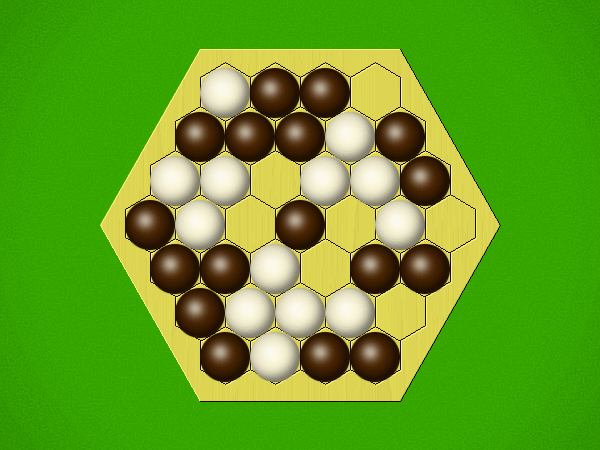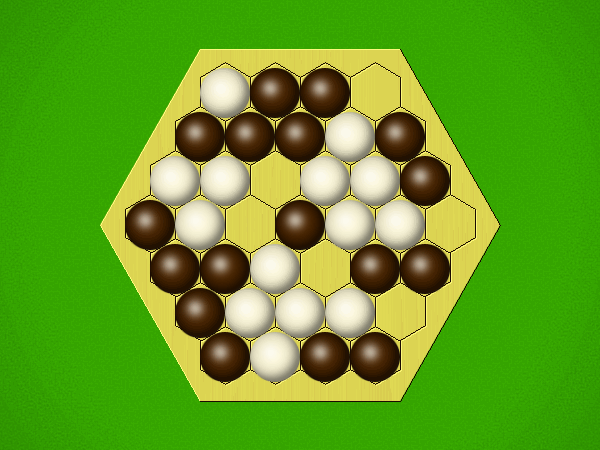
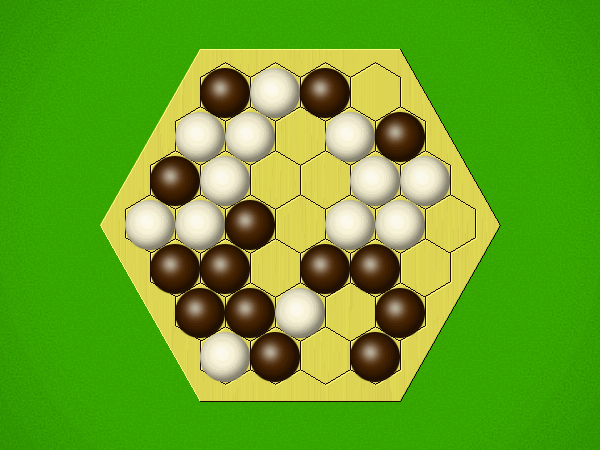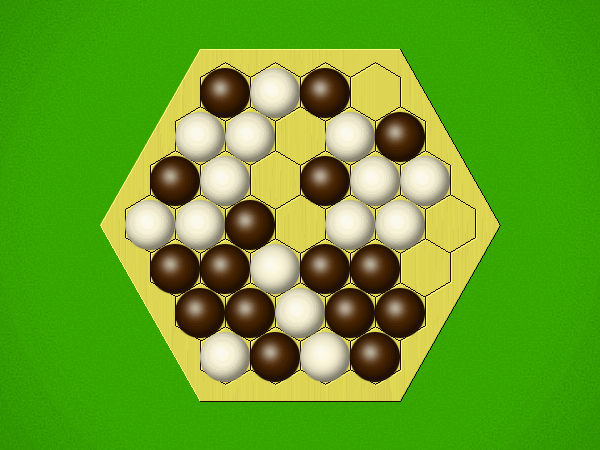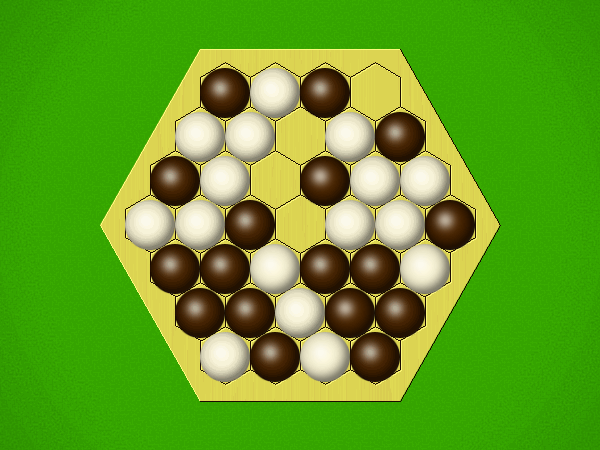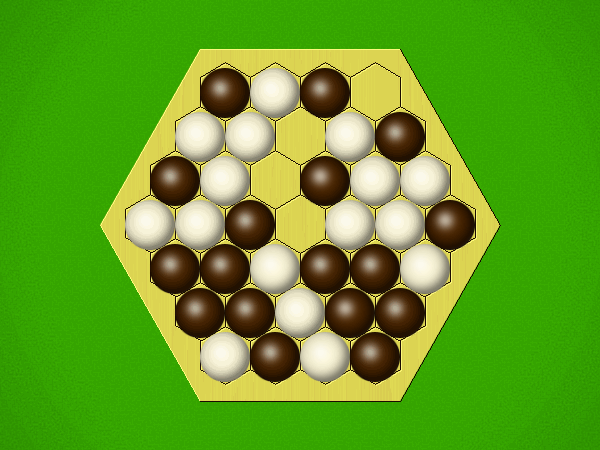
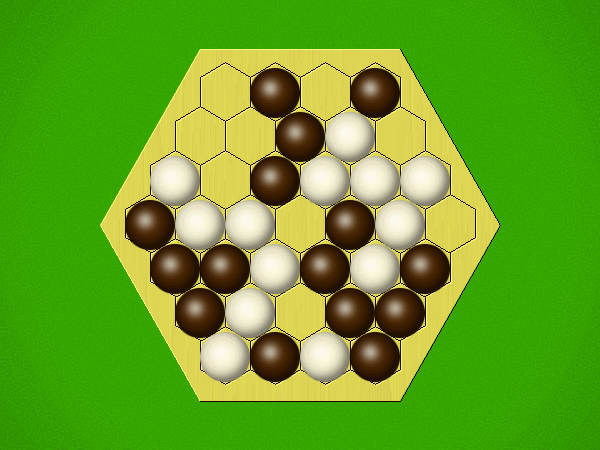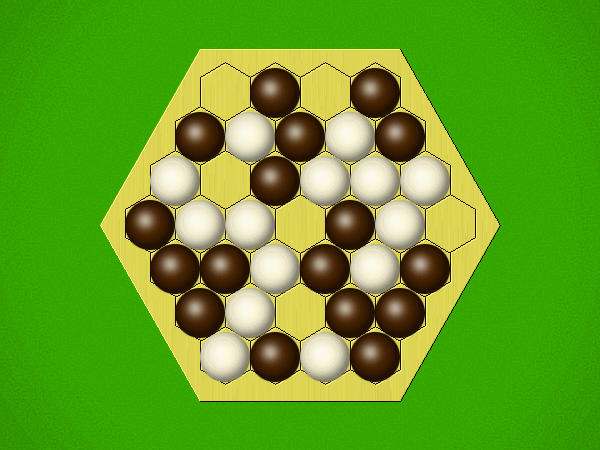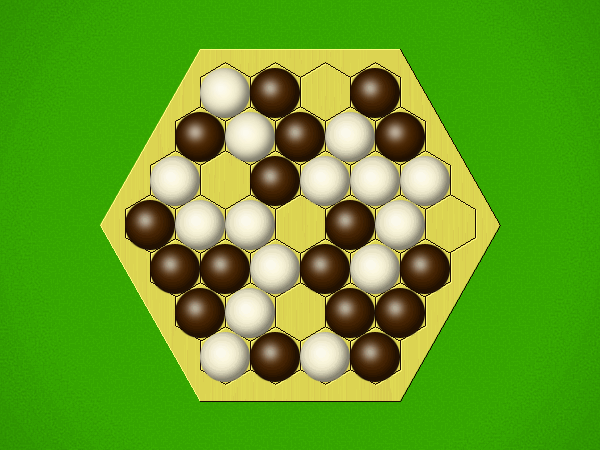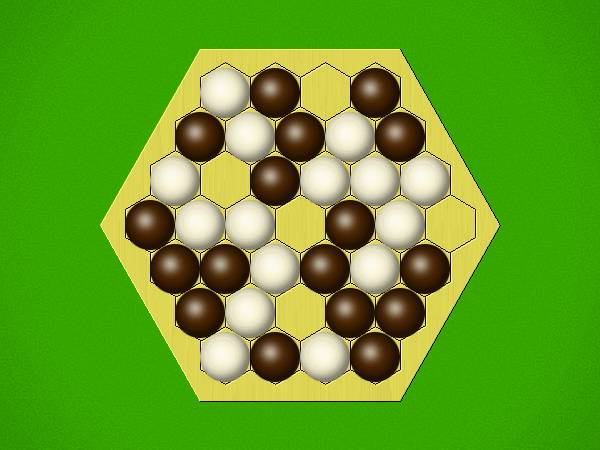
| User | Rating | Comment |
|---|
| bootleby | N/A | My rather 'cold' rating likely has to do with my inability to play this very well, so I'm not getting any insights into the strategic depth since I'm still wearing water wings in the shallow end. I like this game but I don't foresee myself suggesting it? Unless I'm trying to get in as many Nick Bentley games as possible in a day or something I don't know. That is, actually, likely to happen at some point haha |
| mrraow | 10 | Bug is impressively opaque, even on very small boards. But in a good way; the 'perceptual binding' means that the player gets the feeling of understanding being just beyond the horizon, rather than forever beyond reach. Want to play more. Much more :) Playable in Ai Ai (on small boards). Nick kills me - his games are always a real nightmare to programme! In this case, I ended up implementing the game twice. The main problem was identifying when two neighbouring bugs are the same, allowing for reflection and rotation. For the HexHex3 implementation, I tried pre-generating every single board position for each shape, so I could do a straight lookup - that resulted in 2Mb of data after around 60 minutes of processing. Clearly not scalable! For the HexHex4 case, I represented the board as a bitboard (long integer, with each bit representing a different board cell), and did low-level bit manipulation to rotate and compare shapes. The result is fast enough to beat most humans, but unfortunately doesn't scale to larger boards for different reasons*; I may do so at some point using the Java BitSet class (extended to allow shifts) for the bit array, but not for a while. *Ai Ai represents hexhex boards internally as a standard hex grid with the corners missing. That means HexHex5 (61 cells) actually requires 81 bits internally, which is more than a 64-bit integer will hold. |
| nhjelmberg | 9 | I commend the deisgner for a brilliant achievement. This is a game that feels like it was just waiting for someone to discover it. In a time where many designers seem content with copying old mechanics, I am so glad to see that there can be new games under the sun. It will be difficult to return to my own feeble attempts. Thank you for sharing this and good luck with Bug! |
| BobW42 | 8 | Fun, simple, portable game. |
| arian | 7 | |
| fogus | 7.4 | |
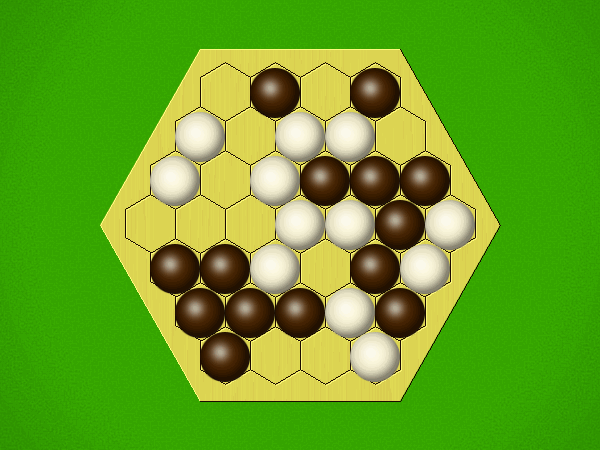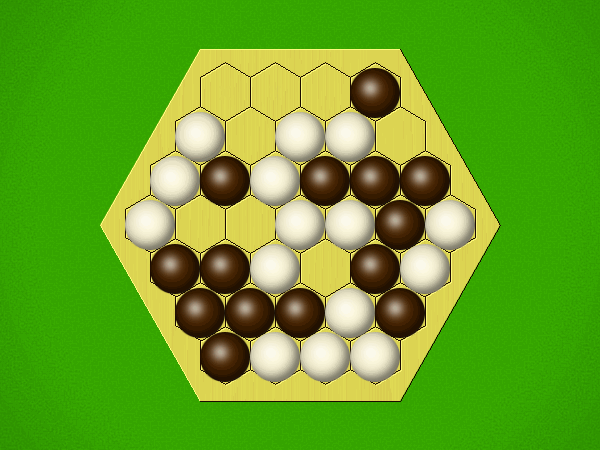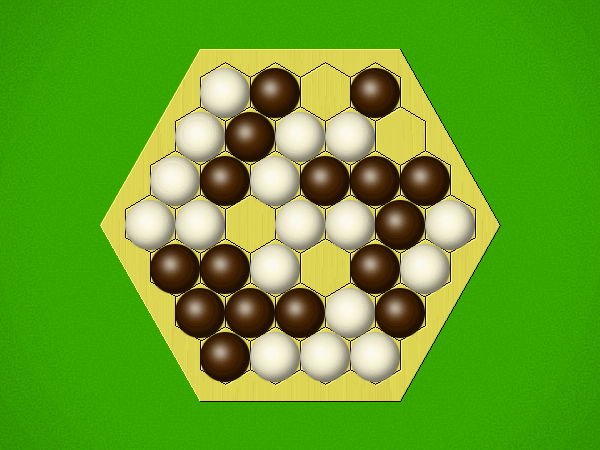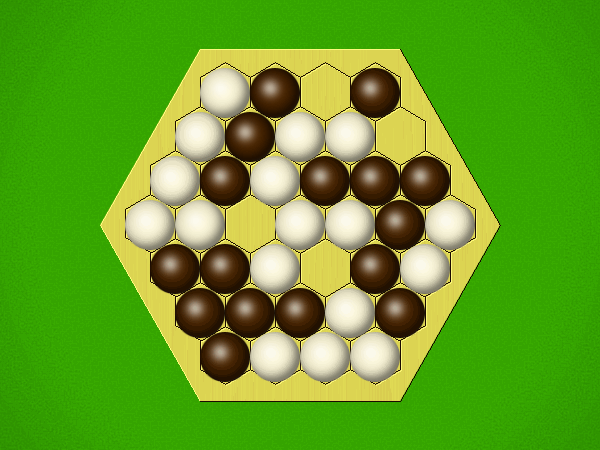
| bcurfs | 8 | This game is a cute abstract strategy with an interesting mechanic. You eat your opponent's bugs and if you can't grow you win (you basically dominate the board). Scalable to different board sizes, but my favorite size for any game on a Hex board is Hexhex-5 (61 fields). That makes the games not too long and still interesting. |
| bothros | 8 | |
| Observer9 | 8 | |
| casualcasual | N/A | I'm not a combinatorial type of player for the most part, but Hive grabbed me, and engaged me. I suspect it's probably those thematic mnemonics. I use the Hive pieces to play Bug, and it's kind of similar; very abstracted but sort of saying something about evolution and expansion. The backwards thinking - of essentially tying to NOT be able to have your turn (probably not unusual, but I just don't have a lot of experience with these sorts of games) is the appealing bit here, to me. A neat little puzzle then; not as engaging and as free form as Hive (again, I don't play a lot of these), but good to be able to pull out and use as something different every now and then. I also should note I'm playing mostly with my son on the 3Hex grid, I'm sure there's a bit more to it on the 4x. |
| molnar | 9 | |
| breakmanynecks | 5 | |
| pvtparts | 6 | |
| luigi87 | 9 | |
| rayzg | 7.5 | Finally played with the correct rules where you win if you cannot place a piece at the beginning of your turn. I'm torn about what I feel about this game. I love how original the mechanics are and how such a deep game could be created with such a small board. My only issue is that there's not much clarity in the game for me. It's really, really difficult to see the repercussions of your moves. I'm hoping that further play will make the tactics more clear. |
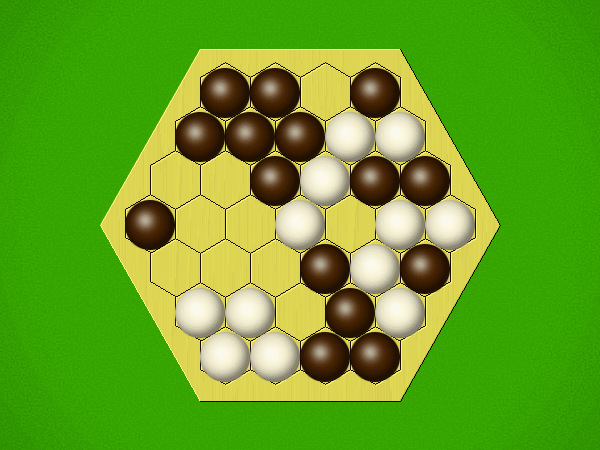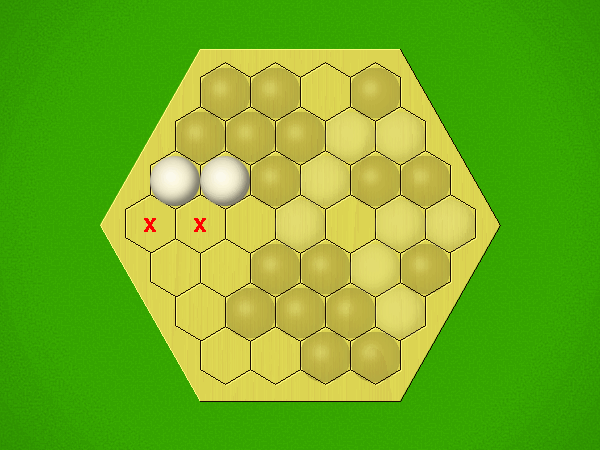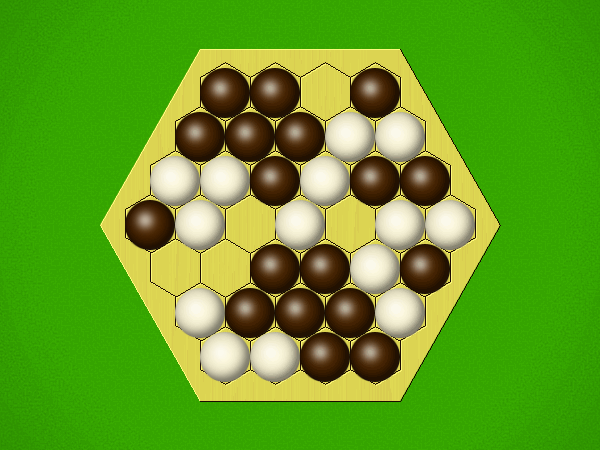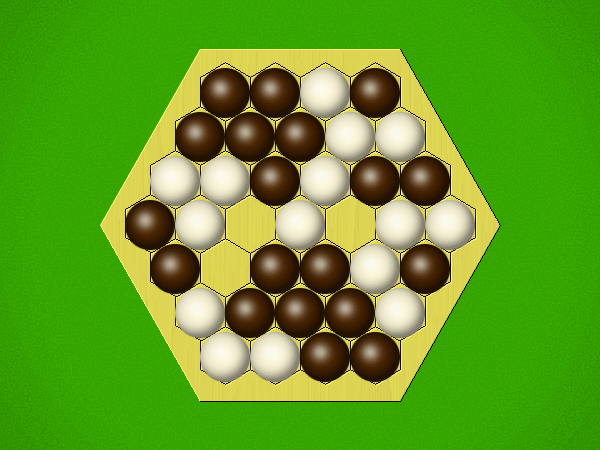
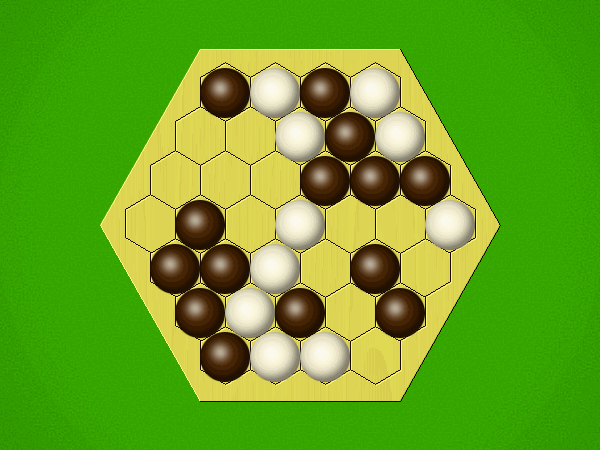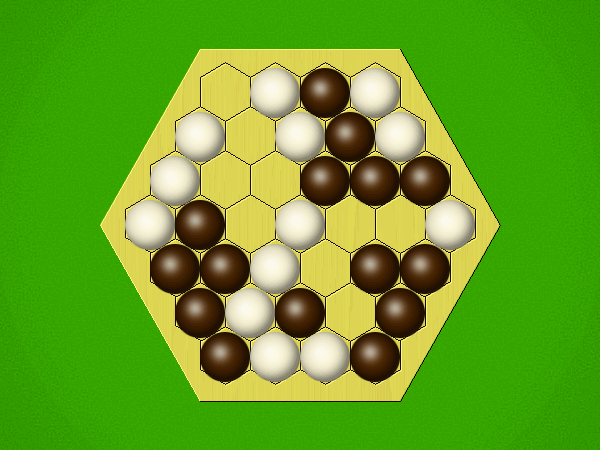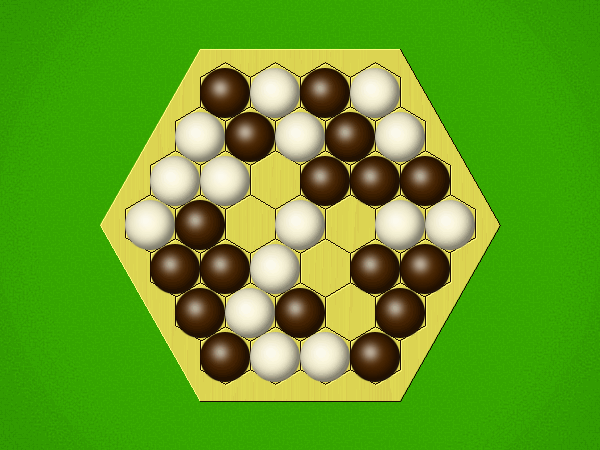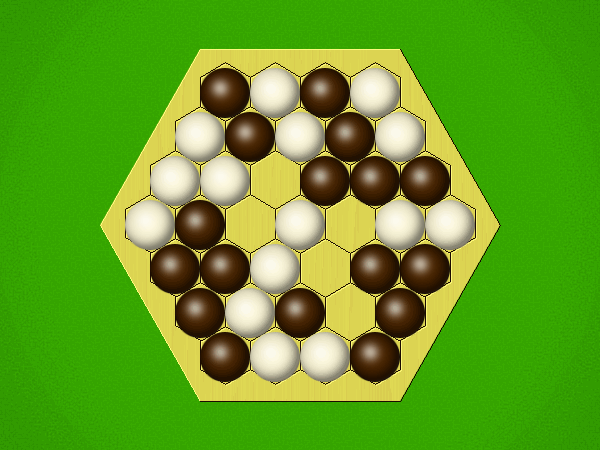
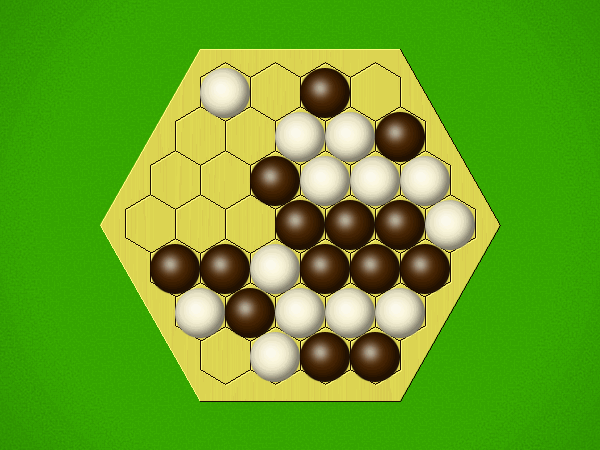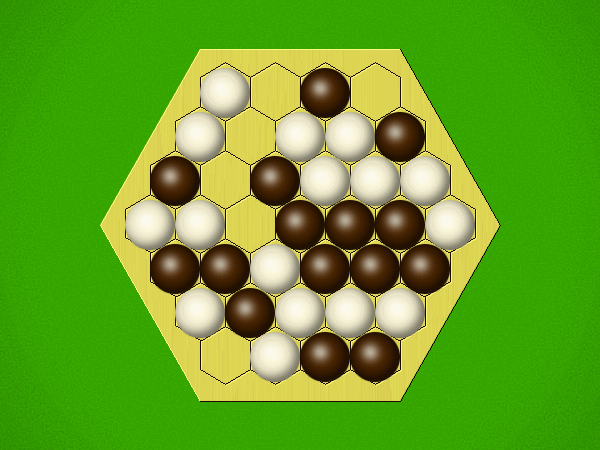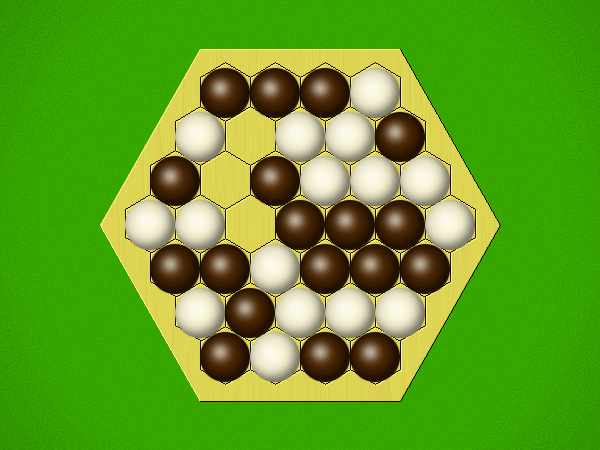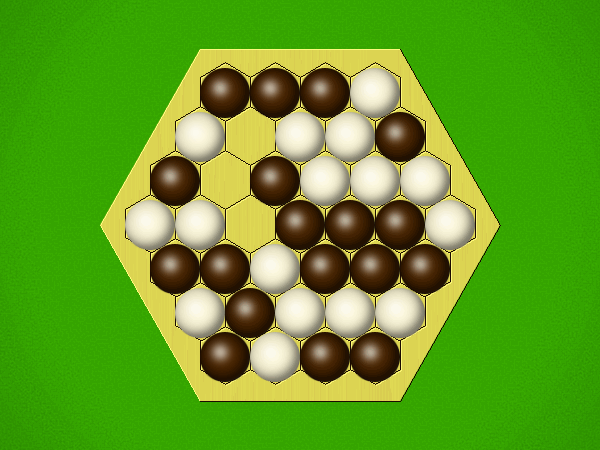
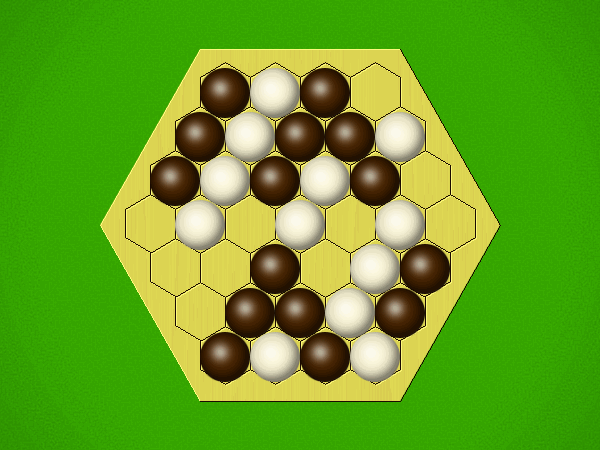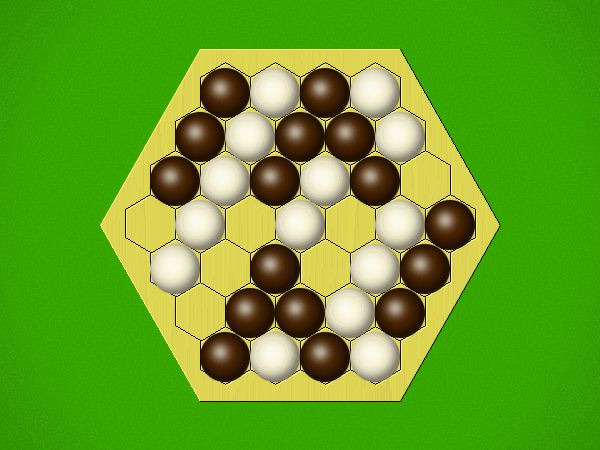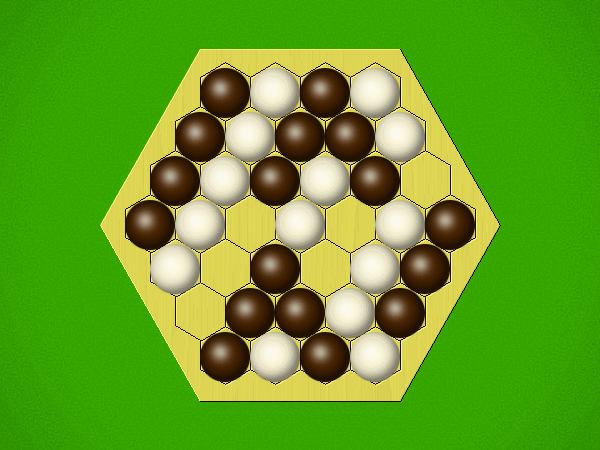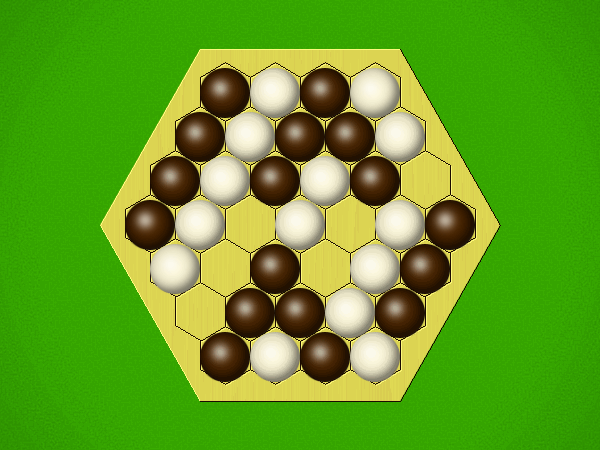
| pkufahl | 7 | I've just scratched the surface of this game, designed around the phenomenon of perceptual binding, our neurobiological tendency to recognize patterns as objects. Bug has several interesting aspects to it: 1. You place markers onto a hex grid, but cannot create the largest group on the board this way. 2. Instead, your groups grow after "eating" your opponents' groups of the same size and shape. 3. Having no legal place on the grid to place your next marker is the way you win the game. I'm always looking for that next abstract game to (at least, temporarily) capture the imagination of myself and one other player, and hopefully I can get in more plays of this one. |
| wefelker | 7 | |
| fakeai | N/A | Print n Play version |
| nycavri | 8 | |
| orangeblood | 8 | Delightful interplay of attacks and counterattacks. At first I wondered about the victory condition (first player who cannot move wins), but after just a couple of games it's pretty intuitive and works well. |
| schwarzspecht | 8 | |
| 4characters | 8 | Unique, innovative |
| nigelreg | 7 | PnP version |
| ed_in_play | N/A | printed HEXn boards to use with Go pieces |
| bcnevan | 7 | This feels so much more organic and natural than Circle of Life, which I did not enjoy at all. Bug scales nicely from beginner games using a small hexhex board to expert games using a larger hexhex board. As far as a comparison to Catchup, which I also like, Bug is a bit less elegant, but brings its own qualities. |
| Matt Booker | N/A | PNP |
| rayr | N/A | = 2017-07-16 Played a couple of split-personality solo games this weekend to learn the rules. I'm liking what I see, but, unlike Yavalath/Pentalath/Manalath, it's going to be a lot harder to see when and where a mistake was made in order to understand how to improve. On a hexhex3 board, it took me about 4 plays to *start* seeing how to improve my chances of being the first player unable to make a move. Fortunately, even if you can't play towards the actual goal (to win by not being able to move), it feels like playing towards the subgoal (eat opponent's bugs) is generally well aligned with the main goal. I'm liking the game. It feels dynamic and I love the tug-o-war. I've noted before that I enjoy games where a seemingly strong move can leave you open to a strategic counter attack. Nick put it even better when he wrote about letting the game balance overly strong moves instead of having the rules forbid them. In Bug, the largest bug on the board is a sitting duck; it can't grow to defend itself so all of the spaces immediately adjacent to that bug are open for your opponent. Those open spaces give you a lot of flexibility, but your ultimate goal is to run out of moves. This means that the closer you get to winning, the fewer options you have. It's an interesting balance and kind of acts like a built-in catch-up mechanism without any heavy-handed rules to enforce it. Playing on a 1999 Abalone board with 7/8" marbles, using a 3rd color to mark off a hexhex3 region. Using the no-merge variant. No rating until I play against a real opponent and start to understand some of the strategies. |
| gmcnish | N/A | Print hexhex3, go stones |
| bdeink | 7 | |
| Carthoris | 8 | A killer combinatorial game with real staying power. |
| grasa_total | 7 | Ingenious and surprising in the way I expect from a Nick Bentley game. But very opaque. I don't think I know what's going on yet. |
| russ | 8 | Clever fun game (be sure to read Nick's article about the game's development) which is interesting even on the tiny size 3 hexhex, and playing on successively larger boards is also cool. It can play out variously (e.g. we had one bizarrely short game with only 6 stones placed, while other games have gradually larger and larger bugs being created), and there are lots of aha-effects to be had. Bug became one of our frequent breakfast games. If you own a small hexhex board and 2 colors of stones (e.g. a Yavalath set), you can play Bug. Note: early on we switched to playing that merging is not legal in placement. Discussion in this thread: https://boardgamegeek.com/thread/1937898/merging-groups-allowed-placement-disallowed-growth |
| paynentt | 8 | |
| Kaelistus | 7 | |
| srlindemann | 8 | |
| javinoa | N/A | DIY |
| hunky dory | 7.5 | |
| fiddly_bits | N/A | I have sufficient bits to play. My board is part of a Chessex mat I cut up long ago to play Hex and other shapes of game. |
| takeoutweight | 9 | I've not played anything like it. One of my favourite modern abstracts. The board can take on so much personality and drama even on a microscopic hex3. I think bug has the best depth-per-board-space ratio out of any game I've played? |
| Bola! | N/A | Subtle! |
| tkvaran | 9 | As of late December 2017, my favorite abstract of 2017. Feels classic and deep. Prefer the 4 hex board to the super tight 3 hex board. |
| njking | 6 | |
| Rontuaru | 8 | Bug is truly unique, remarkable, combinatorial genius. I'll go on and overuse the typical buzzphrases: elegant, clean, clever, sharp, vicious, penseive, brisk...and then some. Pick your praise, because this is as good as abstract games can get. |
| Dawaran | 6.8 | |
| bluebee2 | 9 | PnP. Played with several people and made a few fans of the game (including my college student who it taking it back to school to create more fans)! Loved every game. We're sticking with the hexhex3 for a bit and learning as we go. I'll be playing this quite a bit. |
| conorchinitz | 7 | |
| azeem | 6 | |
| EllenM | 7 | Worth an abstract try We enjoy pulling this one out periodically |
| AndrePOR | N/A | Print & Play Edition |
| pezpimp | 5.5 | You play a piece on the board anywhere as long as it does not create a set larger than any exiting set. If you play a piece in which the size and shape matches an opponents set then you eat them and grow (you have no choice, this is automatic), this is the only way to create larger sets. We played with the correct rules this time around and although better it was not great. We tried a larger board but it just gets repetitive, you can now come from behind and challenge more but can't say that it was more fun. |