Full Report for Dao by Jeff Pickering, Ben VanBuskirk

Rules

Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!

Play

Each turn, slide a piece as far as it will go in a straight line (orthogonally or diagonally).

Goal

You win if you make one of the following patterns:

An orthogonal line of four pieces,
A piece in each corner,
A 2x2 square of your pieces.

You lose if you trap an opponent's piece in a corner.

Miscellaneous

General comments:

Play: Combinatorial

Mechanism(s): Pattern

Components: Board

Level: Standard

BGG Stats

BGG Entry	Dao
BGG Rating	5.31546
#Voters	207
SD	1.71761
BGG Weight	1.5294
#Voters	17
Year	1999

BGG Ratings and Comments

User	Rating	Comment
MrCryptic	6.5
Ebon Wendigo	2	Nice componants but game is broken.
Arcangelurbano	6.5
jchobbs	6
Red Dragon	4.5	About Nine Mens Morris level of simplicity: 8 pieces all the same on a board with 16 spaces all the same. It makes an ok game to pass a little time, if nothing else is available, but that's all this game will ever be.
Geosphere	6	It feels drawish/stalemateish, although I've yet to see it happen.
Willward	6	One of the solved abstracts that still maintains its playability. The deluxe version with a bamboo mat and container is bookshelf-worthy. Nice!
werdynerdy	6
jkgrence	1	Terrible, terrible game. All the strategy and excitement of tic-tac-toe, and costs at least 20 dollars more to boot.
bayspiel	N/A	05.01.01.01
Gnomekin	4.5	Some interesting ideas ultimately flawed by indefinite stalemate conditions.
Sobriquet	4	Many Dao sets are very nice to look at, but the game suffers from stalemates between equal players. Not very engaging as a consequence.
Thaumaturge	6
fogus	4.3	[2015.07.10] I typically like these little, simple abstracts, but this one fell flat for me. The 1PA was too string in my plays.
Kuzai	6
Luke the Flaming	4	[Played once] Simple abstract game that can drag on forever.
weishaupt	6	Decent abstract game. Don't get misled by the simple rules and apparently basic gameplay.
Cognisams	6.5
wispwalker	6
Chrysophylax	1	Futility. Tic-Tac-Toe with stones.. 4x4 instead of 3x3 and movable pieces instead of irrevocably claimed territories. But still Tic-Tac-Toe, and as with Tic-Tac-Toe, the only way an experienced player can win or lose is if someone makes a mistake. [i]"There's no way to win. The game itself is pointless!" - Stephen Falken, WarGames[/i]
AgentJQ	7
jeffwiles	6
Quixote171	4	Feels like advanced Tic-Tac-Toe. Meh.
B Weage	2	Glorified Tic-Tac-Toe that is not only harder to explain (making it less appropriate for the age range that might be able to stand playing it) but also shorter on fun.
sproutgrrl	N/A	X
kenwood77	6
DJZachLorton	N/A	Deluxe version.
PooEater	7
Tikigod	6
sparkin84	7
ellyssian	6	Mr. B was really excited about this game for a while. It's okay, not a favorite.
cad614	6	It's a nice easy game that takes seconds to learn and anyone can play. This is also the game I introduce people to when they ask what type of weird games I play. When not at home I improvise by drawing a "board" on a piece of paper and use coins (heads/tails) as pieces.
gamemark	4	Nicest thing I can say about this simple game... you got a set of those cool Chinese meditation balls to play with.
matthan	3	It appears the only way you can win is if your opponent makes a mistake. Broken Game.
Rozik	6
raymondgwalker	6
penguinofdoom	6
MisterMelon	8
Flamer Shaftglutton	6.7	Quick but surprisingly deep. It may appear similar to tic-tac-toe from the outside, but is considerably deeper than that. You've got to trick your opponent. It's very easy to block your opponent, so you've got to make moves in your favor look like you're blocking your opponent.
Namrok	6
BobDodgerBlue	N/A	1031
jilko	2	Horrible game. Just keep playing until one of you makes a mistake, then the other capitalizes on it. There's no question that it is, in fact, MORE than tic-tac-toe, but that's not very high praise, now, is it?
asekga	8
BeastBen	7	(Version Bamboo) Le jeu est super beau, en deux minute les regles sont expliquer et une partie dure moins de 10 minutes. Si les deux joueurs sont au meme niveau, la partie peut devenir vraiment intense!!!
indigopotter	N/A	New in shrink. Thrift list: http://boardgamegeek.com/geeklist/58758/item/1406670#item1406670
seneca29	6	I see no reason to play this when I can play Farook. Dao seems solvable and prone to drawish stalemate (homemade)
parliboy	N/A	4x4 board equals not a lot of decision-making in an abstract game where pieces have no powers. But it was a gift, and it's the thought that counts.
LosSchabossDragon	10
CarlosLuna	8
pattonre	7	Another game that I never bothered to spend money on for an artsy and expensive set. Made my own to play.
Gamethyme	6
TempNinjaLee	6
chuji	7
Graybillion	6
Bien	5	Abstract
strings	5	Seems like a pleasant enough little filler, stones make a satisfying sound as you slide them across the bamboo.
ecoboardgeek123	6.5
kgnunn	6
Janik013	7
kimba	6
Super633K	7
Lejade	4	I own a very nice "bamboo box & smooth stones" edition of this game. Unfortunately gameplay isn't as nice. It reminds me of chinese tic-tac-toe in the sense that when two decent players compete, the game will keep going as the players circle each other waiting for a mistake... which may never come!
dancingdanslc	4	DIGITAL PLAY: iPad Air Abstract strategy game. Boring abstract Out of my collection
lwheeler	3	(harmony ball version) The components are nice, but not for this game! The game never ends.
Blue Steel	7
Connatic	6
laurentdeenen	5	2p
Talisinbear	5	OK light filler
Drewopoly	N/A	Complete
herace	10
Ikarus	N/A	# P&P
Skyjack	7
bmuchortow	6.5
rtrowan	6
djnesq	4	I'm not sure you can force a win in this game, even with perfect play. You have to wait for the other guy to make a mistake.
ssortiz	7
Caribbean	6	Good game!
LtSykes	5	I have a lot of mixed feelings for this game. I got it when I was on a kick, looking for new abstract strategy games. I wish I had known all the rules and pieces before hand, because I didn't need to waste twenty bucks on this since I could have made it myself. That being said it is easy to take everywhere and is surprisingly deep psychologically for a game that doesn't have much to it.
starfox634	6
hippiephysicschick	N/A	2p abstract thrifted No box in knight moves
Eric Ridley	4.9	Seems like this game could devolve in to just moving for the sake of moving. And it did with me.
davidabradley	9
Grainknight	7
ProgressorM	4	Has obvious flaws
amtorgerson	6
Drewcooter	6	Nice bits, cool abstract, my 11 year old daughter really digs it,
Choukou	7
ElHijodeEloisa	7
Asmoridin	5	I've only played it once, and it was pretty good for the one game. Allowing the whole '4 corners' set-up being a win condition was nice (for my opponent), as I totally didn't even see it coming, meaning you can get some good bluffing in. However, I really think this game would lose some of its replay value if I played it more often. I could just see myself having less and less fun with more plays.
astanix	6.5
arhenius	6
SOCIOJEUX	N/A	Sur les tablettes de l'Espace Sociojeux
SaraStorm	8
Nap16	6	Free Print & Play. Awards: Mensa Select 2001.
PnoiKoji	7
Teriyaki Donuts	N/A	Needs to be played.
zodball	6
plaidpants	2	Easy to make a homemade version. Similar to Brandubh which is better.
amwiles	6	An okay abstract. Very portable, but I wouldn't want to play it more than twice in a row. Games can take too long against equally matched players. Flinching is bad.
D Erasmus	3	Keeps my kids busy quite a bit. Not much fun as they got older. Game can go on forever as the strategy is pretty simple.
Galion	6	I don't fully understand the rules, despite, or perhaps because of, their brevity.
AlexBeresford	6
kromatic	7	Two-player game that can be taught in two minutes, but allows for as much depth as the players can imbue. (Rated relative to other 2p games)
MrKorky	7
JuliaZ	6.5
Impr3ssion	6	Beats tic-tac-toe! My brother got this for me as a gift, and I like that version's glass pieces and mouse-pad board. The difficulty of trying to win without giving the other person an opening makes this an intense game. I know it's solved and whatnot, but I like it.
rampantdragon	6
hojoh	N/A	F
kaiser	5	Interesting and quick game for 2 players
The Abstractionist	N/A	Comes in a metal box.
Salabesh	6
tetsuo13	6
fxcafe	9
gjfleischman	8
bhorner	7.5
MrTacoBueno	7
markus_kt	3	More a puzzle than a game.
Austincd27	8
KyleWyatt	7	Simple gameplay, but very engaging. Gametime varies on how long it takes someone to make one simple mistake.
amortera	8	1
Conmoy	7
CDRodeffer	3	As it is, the game is almost certainly a forced draw, and thus broken, except for the uninitiated. But perhaps it could be fixed? One possibility would be to give each player an initial number of chips (say, 3) that could be used to strategically stop a piece before it hits a wall or another piece. With some tweaking, my rating for Dao may improve.
Quentak	7
Larryfromcarync	6
darthnice	6
aewhite	6
vandemonium	7	Gift from the in-laws. I had asked for Grass - not realizing - really! - of the pot reference. :shake: Anyhow, they got this for me instead :blush: and it is a nifty little abstract. The wife and I have played it quite a bit. Recommended for a light, quick, fun abstract. I'd call it a filler abstract. That is not pejorative - it just is a quick fun little game. And it has no references to drugs, at least of which I am aware :shake:
LudoMC	6
fazerfora	N/A	$3
Audiovore	9
jjferry1974	N/A	Checked & is complete
wookie1	2	Hmmm...The game is better then tic-tac-toe...but not by much. Update: This game is a totalal yawn fest....I actually threw this game out in the garbage ...good riddance!
jobby	6
pulla	5	I just don't like abstracts. Rating based on just one play.
Mike_Rutch	7
runicfox	7
d3jg	8.5
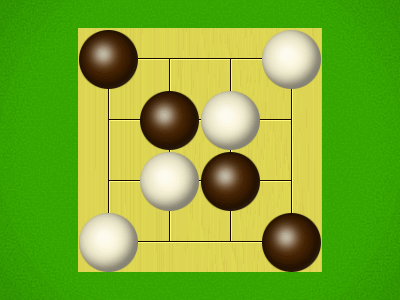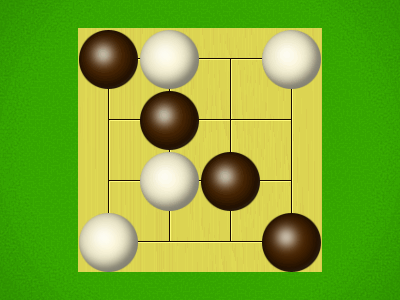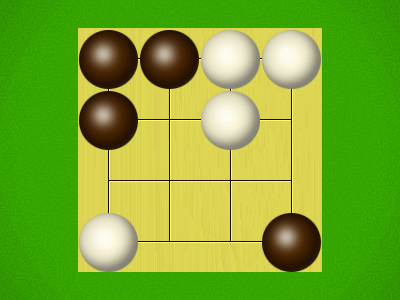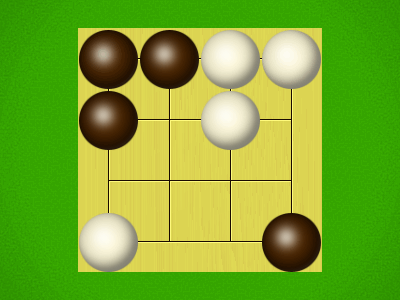
gr9yfox	4	Very simple abstract game with a streamlined rule set. Push pieces as far as they can move in a single direction and try to achieve one of the three possible ending conditions. It is easy to get into stalemates and the optimal move is obvious most of the time.
MeepleMaven	5.5	Bamboo mat version - needs quality components to enhance game play.
red_mary	N/A	Nicolas
szoffi	N/A	mi ez, jo ajandeknak?
Kaffedrake	4	Small tactical abstract where pieces slide on ice. Superficially similar to Farook, which I would prefer.
croyalporter	7	Quick and pretty fun. Just don't be the first one to make a mistake.
Count Gregor	6
Rolwin	6
NanaChris	N/A	Sean taught me how to play this using the Ceega board
emaverie	8
dbucak	3	Degenerates into a stalemate fairly quickly.
fokos	6.5	A nice abstract game for two.Unfortunately is gives me the feeling that its determined by the first mistake
SEb.	6
finallyiamnoone	7
JeffStone	6
ScaperDeage	6
AndrePOR	N/A	Print & Play Edition
boujacahin	8	You have to have nerves of steel and tons of patience for this game because unlike chess or go, the board is much smaller and pieces are not added or removed. Each move has to be offensive and defensive. People who only focusing on what they do will lose, as will those who only focus on what the opponent does.

Kolomogorov Complexity Analysis

Size (bytes)	23450
Reference Size	10293
Ratio	2.28

Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.

Playout Complexity Estimate

Playouts per second	59456.92 (16.82µs/playout)
Reference Size	534016.87 (1.87µs/playout)
Ratio (low is good)	8.98

Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.

Playout/Search Speed

Label	Its/s	SD	Nodes/s	SD	Game length	SD
Random playout	100,659	872	2,704,120	23,483	27	6
search.UCT	99,832	5,636			30	0

Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.

Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.

Mirroring Strategies

Rotation (Half turn) lost each game as expected.
Reflection (X axis) drew against Grand Unified UCT(U1-T,rSel=s, secs=1.00) playing 1st, moves: [b2-a2, c2-d2, a2-a3, d2-c1, c3-c4, c1-d2, d4-d3, b3-b4, a3-a2, a4-c2, c4-b3, b4-a4, d3-d4, d2-c1, a2-b1, c2-d2, b1-b2, d2-b4, d4-d2, c1-b1, b2-a3, b4-d4, a3-c1, b1-d3, c1-a3, d3-b1, a3-c1, b1-b2, d2-d3, b2-b1]
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.

Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.

Win % By Player (Bias)

1: White win %	50.90±3.10	Includes draws = 50%
2: Black win %	49.10±3.09	Includes draws = 50%
Draw %	93.40	Percentage of games where all players draw.
Decisive %	6.60	Percentage of games with a single winner.
Samples	1000	Quantity of logged games played

Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)

Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.

UCT Skill Chains

Match	AI	Strong Wins	Draws	Strong Losses	#Games	Strong Score	p1 Win%	Draw%	p2 Win%	Game Length
0	Random
3	UCT (its=4)	342	578	58	978	0.6147 <= 0.6452 <= 0.6746	18.61	59.10	22.29	25.51
9	UCT (its=10)	441	380	174	995	0.6038 <= 0.6342 <= 0.6635	30.55	38.19	31.26	23.32
12	UCT (its=33)	537	188	253	978	0.6147 <= 0.6452 <= 0.6746	39.98	19.22	40.80	19.96
14	UCT (its=241)	572	118	54	744	0.8205 <= 0.8481 <= 0.8721	41.53	15.86	42.61	19.10
18	UCT (its=13160)	320	621	5	946	0.6358 <= 0.6665 <= 0.6958	16.17	65.64	18.18	25.09
19	UCT (its=35771)	2	517	2	521	0.4572 <= 0.5000 <= 0.5428	0.19	99.23	0.58	29.96
20	UCT (its=35771)	1	998	1	1000	0.4691 <= 0.5000 <= 0.5309	0.10	99.80	0.10	29.98

Search for levels ended. Close to theoretical value: draw.

Level of Play: Strong beats Weak 60% of the time (lower bound with 95% confidence).

Draw%, p1 win% and game length may give some indication of trends as AI strength increases.

1st Player Win Ratios by Playing Strength

This chart shows the win(green)/draw(black)/loss(red) percentages, as UCT play strength increases. Note that for most games, the top playing strength show here will be distinctly below human standard.

Complexity

Game length	29.09
Branching factor	10.77
Complexity	10^29.72	Based on game length and branching factor
Computational Complexity	10^5.39	Sample quality (100 best): 49.94
Samples	1000	Quantity of logged games played

Computational complexity (where present) is an estimate of the game tree reachable through actual play. For each game in turn, Ai Ai marks the positions reached in a hashtable, then counts the number of new moves added to the table. Once all moves are applied, it treats this sequence as a geometric progression and calculates the sum as n-> infinity.

Move Classification

Board Size	16	Quantity of distinct board cells
Distinct actions	152	Quantity of distinct moves (e.g. "e4") regardless of position in game tree
Good moves	98	A good move is selected by the AI more than the average
Bad moves	54	A bad move is selected by the AI less than the average
Response distance	1.77	Mean distance between move and response; a low value relative to the board size may mean a game is tactical rather than strategic.
Samples	1000	Quantity of logged games played

Board Coverage

A mean of 91.04% of board locations were used per game.

Colour and size show the frequency of visits.

Game Length

Game length frequencies.

Mean	28.16
Mode	[29]
Median	29.0

Change in Material Per Turn

Mean change in material/round	0.00	Complete round of play (all players)

This chart is based on a single representative* playout, and gives a feel for the change in material over the course of a game. (* Representative in the sense that it is close to the mean length.)

Actions/turn

Table: branching factor per turn, based on a single representative* game. (* Representative in the sense that it is close to the mean game length.)

Action Types per Turn

This chart is based on a single representative* game, and gives a feel for the types of moves available throughout that game. (* Representative in the sense that it is close to the mean game length.)

Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.

Trajectory

This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).

The lead changed on 34% of the game turns. Ai Ai found 9 critical turns (turns with only one good option).

Position Heatmap

This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).

Good/Effective moves

Measure	All players	Player 1	Player 2
Mean % of effective moves	73.42	59.14	88.72
Mean no. of effective moves	8.03	6.60	9.57
Effective game space	10^22.86	10^9.65	10^13.21
Mean % of good moves	6.24	7.91	4.44
Mean no. of good moves	0.72	0.93	0.50
Good move game space	10^1.68	10^1.08	10^0.60

These figures were calculated over a single game.

An effective move is one with score 0.1 of the best move (including the best move). -1 (loss) <= score <= 1 (win)

A good move has a score > 0. Note that when there are no good moves, an multiplier of 1 is used for the game space calculation.

Quality Measures

Measure	Value	Description
Hot turns	89.66%	A hot turn is one where making a move is better than doing nothing.
Momentum	17.24%	% of turns where a player improved their score.
Correction	41.38%	% of turns where the score headed back towards equality.
Depth	2.07%	Difference in evaluation between a short and long search.
Drama	0.03%	How much the winner was behind before their final victory.
Foulup Factor	10.34%	Moves that looked better than the best move after a short search.
Surprising turns	10.34%	Turns that looked bad after a short search, but good after a long one.
Last lead change	72.41%	Distance through game when the lead changed for the last time.
Decisiveness	24.14%	Distance from the result being known to the end of the game.

These figures were calculated over a single representative* game, and based on the measures of quality described in "Automatic Generation and Evaluation of Recombination Games" (Cameron Browne, 2007). (* Representative, in the sense that it is close to the mean game length.)

Openings

Moves	Animation
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-d2,b2-c2,b3-a3,b4-c4,d2-b4
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-d2,b2-c2,b3-a3,b4-c4,a3-c1
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-d2,b2-c2,b3-a3,b4-b1,d2-b4
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-d2,b4-c4,d2-b4,b2-c3,b3-a3
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-d2,b4-c4,d2-b4,b2-c3,b4-a3
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-d2,b4-c4,d2-b4,b2-b1,b3-a3
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-c1,b4-c4,b3-b4,b2-c3,c1-a3
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-c1,b4-c4,b3-b4,b2-c3,c1-d2
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-c1,b4-c4,b3-b4,b2-c3,d1-b3
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-c1,b4-c4,b3-d3,b2-c3,c1-a3
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-c1,b4-c4,b3-c2,b2-c3,c1-a3
a1-a3,d1-d3,a3-a1,d3-d1,c3-b4,c2-c1,b4-c4,b3-c2,b2-c3,c1-d2

Opening Heatmap

Colour shows the success ratio of this play over the first 10moves; black < red < yellow < white.

Size shows the frequency this move is played.

Unique Positions Reachable at Depth

0	1	2	3	4	5	6	7	8	9	10	11
1	12	152	1304	9561	43443	173755	484642	1100985	1921091	2816608	3717371

Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.

Shortest Game(s)

244 solutions found at depth 5.

Puzzles

Puzzle	Solution
White to win in 5 moves
Black to win in 3 moves
Black to win in 3 moves
Black to win in 3 moves
White to win in 3 moves

Weak puzzle selection criteria are in place; the first move may not be unique.

State Space Complexity

% new positions/bucket

State Space Complexity	9068157
State Space Complexity (log 10)	6.96
Confidence	83.22	0: totally unreliable, 100: perfect
Samples	1143977

State space complexity (where present) is an estimate of the number of distinct game tree reachable through actual play. Over a series of random games, Ai Ai checks each position to see if it is new, or a repeat of a previous position and keeps a total for each game. As the number of games increase, the quantity of new positions seen per game decreases. These games are then partitioned into a number of buckets, and if certain conditions are met, Ai Ai treats the number in each bucket as the start of a strictly decreasing geometric sequence and sums it to estimate the total state space. The accuracy is calculated as 1-[end bucket count]/[starting bucklet count]