Don't lose.
The board starts empty. Each player takes the four pieces of a single color to form her supply: Player 1 takes white; Player 2 takes black.
Note: In this game, the term line includes the circle and its arcs.
If no one loses the game before all pieces are on the board (Placement Phase), the game will continue into a Movement Phase.
On your turn, you must stack a piece from your supply atop one of the spaces (which represent the points) on the board, respecting this Stacking Rule: The space you select must have no more than two pieces on it, and none of them can be both the same color and the same shape as the piece you are adding. For example, you could add your white triangle to any of the following:
...but neither to a space with a white triangle, nor to a space with 3 pieces on it already.
On your turn, you must move one of your topmost pieces from a stack along a line to an adjacent space, respecting the Stacking Rule.
You lose the game if, on your turn, any of the following are true:
At the end of your turn, there are three topmost pieces of the same color, or three topmost pieces of the same shape on the same line (remember, the circle is a line).
In the Movement Phase, you are unable to move a piece, because no stack has one of your pieces as its topmost piece at the start of your turn.
If a repetition of moves occurs in the Movement Phase, the game ends in a draw; play the game again, swapping turn order.
General comments:
Play: Combinatorial
Family: Combinatorial 2016
Mechanism(s): Pattern,Stacking
Components: Board
| BGG Entry | Fano330-R-Morris |
|---|---|
| BGG Rating | 6.82 |
| #Voters | 25 |
| SD | 1.92811 |
| BGG Weight | 2 |
| #Voters | 3 |
| Year | 2016 |
| User | Rating | Comment |
|---|---|---|
| bootleby | N/A | High rating is mostly for novelty but also I want to play this more! |
| ddash | 7 | |
| d5884jp | 6 | |
| mrraow | 6 | Simple, and treacherous; so many ways to die, and so few ways to live. |
| jcfiala | N/A | Well, insofar as I have Pyramid Arcade... |
| clark94 | 6 | Feels like being tossed into a meat grinder but is enjoyable. |
| Forianst | 6 | |
| fogus | 5.5 | In a far-off universe on a lonely planet in a nondescript system of planets is a futuristic society far more advanced than our own. If on this planet they have a game that fills the same niche as Tic-Tac-Toe then it would not surprise me one iota if that game was Fano330-R-Morris. Indeed, I would imagine that on this planet citizens carry playing stones carved from fine minerals and stones stored on their persons in soft leather pouches made from the finest ganth skins. When one citizen wishes to challenge another in a Fano330-R-Morris match the pouches are flashes and a board drawn from memory. The stakes may be high, but yet a winner will be determined in mere moments. |
| pleclenuesse | 7 | |
| Fred_Beavon | N/A | I love the design of Fano330-R-Morris and its simple rules. But, what's to stop the second player from placing one of his pieces on top of every piece the first player places on the board, thus winning the game, since the first player will then not be able to move? |
| russ | 8 | Surprising fun short clever little game - more to it than meets the eye. Surprisingly quick defeats sometimes, even during the initial placement phase, and sometimes protracted maneuvering in the movement phase before someone finally loses. We often play several times in a row. |
| tsaito | 8 | |
| ceenan | 6 | |
| Arcanio | 7 | |
| tokoro | 9 | A simple, but beautiful game! |
| danrodz | 7.5 | Clever abstract, very enjoyable |
| zefquaavius | 9 | Such simple, simple rules, and such tricky play! There are only 7 spaces, and only 7 "lines" along which you can lose in this reverse-morris game… but it's incredibly easy to do. Setting your opponent up to lose is the usual extra layer of abstraction. |
| Smjj | 1 | |
| nestorgames | 9 | |
| rayzg | 8 | Very clever! |
| ivan111 | N/A | простой маленький абстракт |
| LurkingMeeple | 7 | The unwieldy name, cold appearance, and emphasis on losing were initial turnoffs, but the play is exceptionally good for its size. It was fun to play this and [boardgame=4643]Fire and Ice[/boardgame] back-to-back. |
| PBiensan | 9 | Deceptively simple-looking but really clever abstract. The victory conditions really make the game mindblowing to play. In the same category as "Lines of Action". |
| Kaffedrake | 3 | I am not fond of abstracts that consist of comparably small yet difficult to parse decision trees. First you read the current board state to see which legal and non-losing moves are available; then you read the future board states to see if any of these leave your opponent without a legal and non-losing move; then, if you're not sick of the topography yet, you read the future future board states to see if there's anything resembling strategy up ahead, except you already lost on your last move. |
| orangeblood | 6 | |
| carmenpf7 | 8 | |
| akat | 10 | I like Triangle mechanical Feeling! |
| hojoh | N/A | D |
| Jyothi | N/A | Just discovered a whole new world of games! Will need some more research. |
| glanfam | 5 | Very quick abstract game. Have a feeling it can be solved. But not by me. Clarity is nonexistent. Have no clue what I'm doing. Which is odd for such a small board with simple rules. |
| AndrePOR | N/A | Print & Play Edition |
| The Player of Games | 6.5 | Unusual game as you win by forcing your opponent to lose. This feels like a real, playable game in the niche that Tic-Tac-Toe lives in. |
| infomage27 | N/A | (piracy contender, do not buy) |
| AI | Strong Wins | Draws | Strong Losses | #Games | Strong Win% | p1 Win% | Game Length |
|---|---|---|---|---|---|---|---|
| Random | |||||||
| Grand Unified UCT(U1-T,rSel=s, secs=0.01) | 36 | 0 | 0 | 36 | 100.00 | 47.22 | 8.19 |
Level of Play: Strong beats Weak 60% of the time (lower bound with 90% confidence).
Draw%, p1 win% and game length may give some indication of trends as AI strength increases; but be aware that the AI can introduce bias due to horizon effects, poor heuristics, etc.
| Size (bytes) | 24878 |
|---|---|
| Reference Size | 10577 |
| Ratio | 2.35 |
Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.
| Playouts per second | 265886.73 (3.76µs/playout) |
|---|---|
| Reference Size | 1914975.11 (0.52µs/playout) |
| Ratio (low is good) | 7.20 |
Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.
| 1: White win % | 56.32±2.47 | Includes draws = 50% |
|---|---|---|
| 2: Black win % | 43.68±2.44 | Includes draws = 50% |
| Draw % | 32.18 | Percentage of games where all players draw. |
| Decisive % | 67.82 | Percentage of games with a single winner. |
| Samples | 1566 | Quantity of logged games played |
Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)
Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.
Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.
Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.
| Game length | 23.77 | |
|---|---|---|
| Branching factor | 8.05 | |
| Complexity | 10^19.90 | Based on game length and branching factor |
| Samples | 1566 | Quantity of logged games played |
| Distinct actions | 44 | Number of distinct moves (e.g. "e4") regardless of position in game tree |
|---|---|---|
| Good moves | 27 | A good move is selected by the AI more than the average |
| Bad moves | 17 | A bad move is selected by the AI less than the average |
| Samples | 1566 | Quantity of logged games played |
This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).
The lead changed on 38% of the game turns. Ai Ai found 7 critical turns (turns with only one good option).
Overall, this playout was 61.11% hot.
This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).
Table: branching factor per turn.
This chart is based on a single playout, and gives a feel for the types of moves available over the course of a game.
Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 14 | 210 | 1890 | 14826 | 66906 | 267246 | 624666 | 1228206 | 1831170 | 1583377 | 1831170 | 1554708 | 1831436 | 1563658 | 1831387 | 1563428 |
Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.
42 solutions found at depth 3.
| Moves | Animation |
|---|---|
| Round6,Triangle3,Round7,Triangle1,Triangle4,Round5,Triangle1,Round6,7-5,3-7 |  |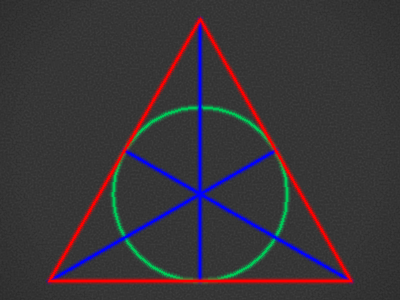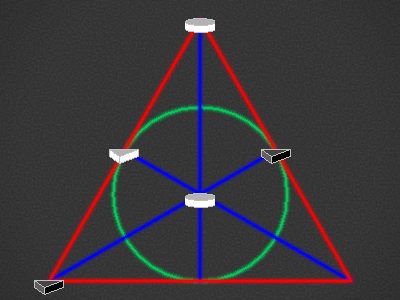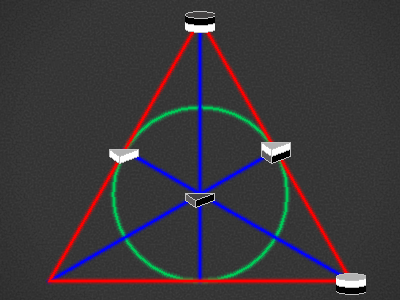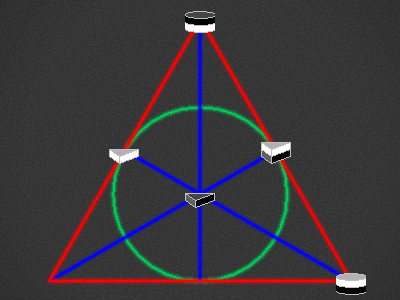
| Round6,Triangle5,Round4,Triangle7,Triangle2,Round1,Triangle5,Round7,2-4,1-6 |  |
| Round6,Triangle5,Round4,Triangle7,Triangle1,Round2,Triangle7,Round4,1-5,2-1 |  |
| Round6,Triangle5,Round2,Triangle1,Triangle4,Round3,Triangle5,Round1,4-6,3-7 |  |
| Round6,Triangle5,Round2,Triangle7,Triangle3,Round1,Triangle6,Round5,3-4,7-2 |  |
| Round6,Triangle4,Round2,Triangle7,Triangle1,Round6,Triangle7,Round2,1-4,2-3 |  |
| Round6,Triangle2,Round4,Triangle7,Triangle1,Round5,Triangle7,Round4,1-5,2-1 |  |
| Round6,Triangle2,Round1,Triangle7,Triangle4,Round3,Triangle7,Round1,4-3,2-4 |  |
| Round6,Triangle2,Triangle7,Round2,Round1,Triangle3,Triangle4,Round3,7-6,2-4 |  |
| Round6,Triangle1,Round2,Triangle5,Triangle4,Round3,Triangle5,Round1,4-6,3-7 |  |
| Round6,Triangle1,Round2,Triangle7,Triangle4,Round6,Triangle7,Round2,4-1,2-5 |  |
| Round6,Triangle1,Round7,Triangle3,Triangle4,Round5,Triangle1,Round6,7-5,3-7 |  |