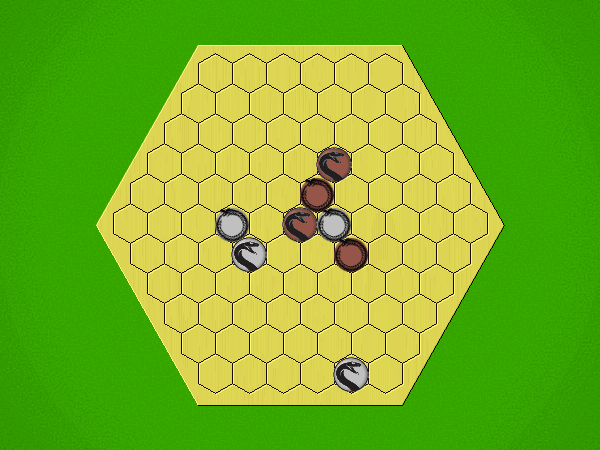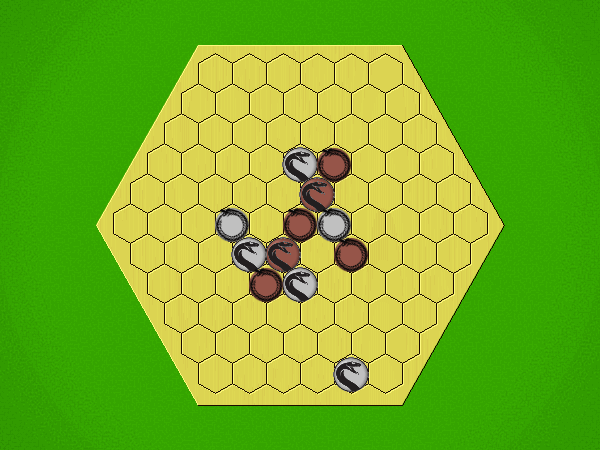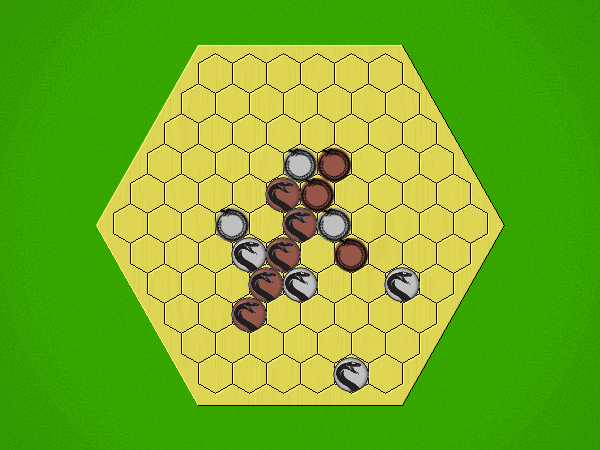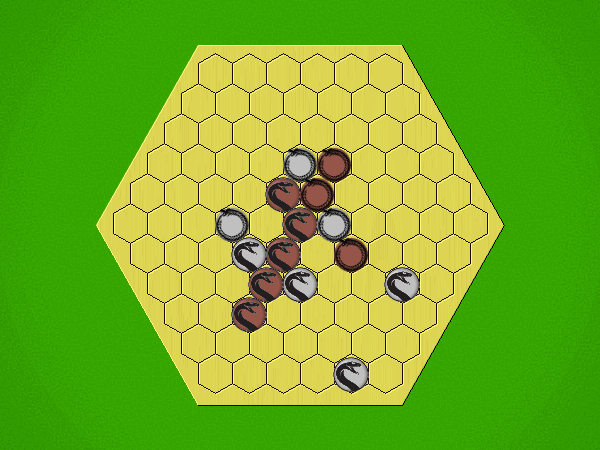
Full Report for Flipping by Stephen Tavener

Rules

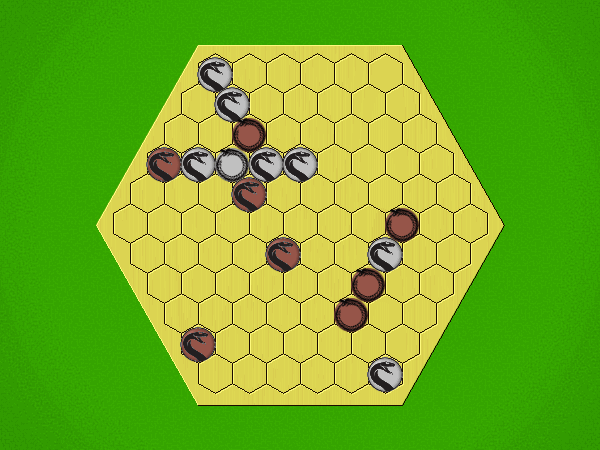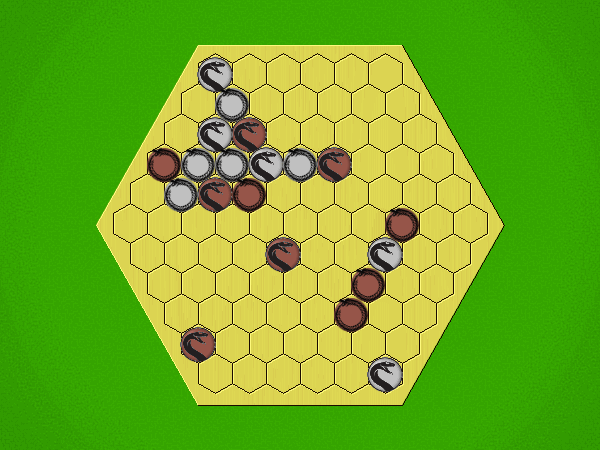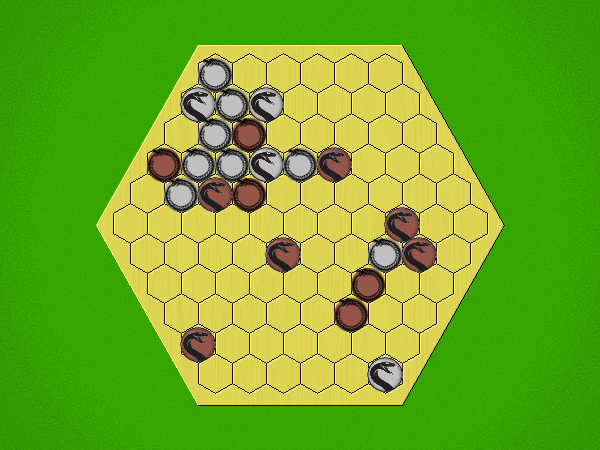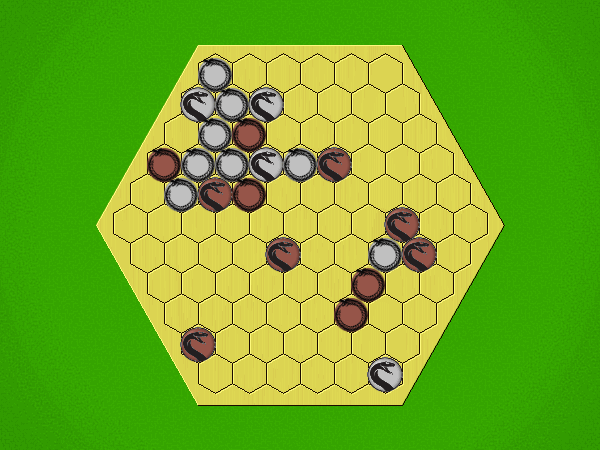
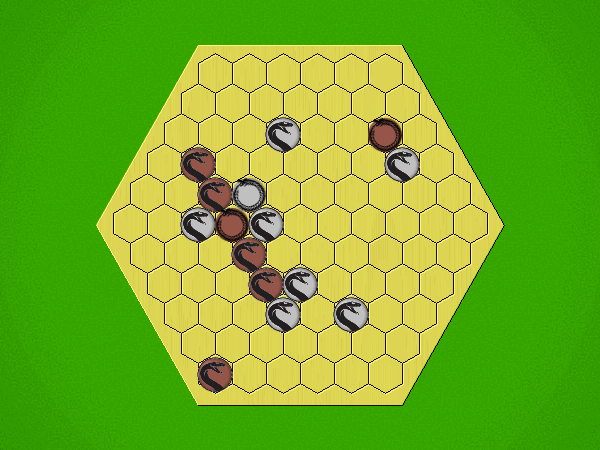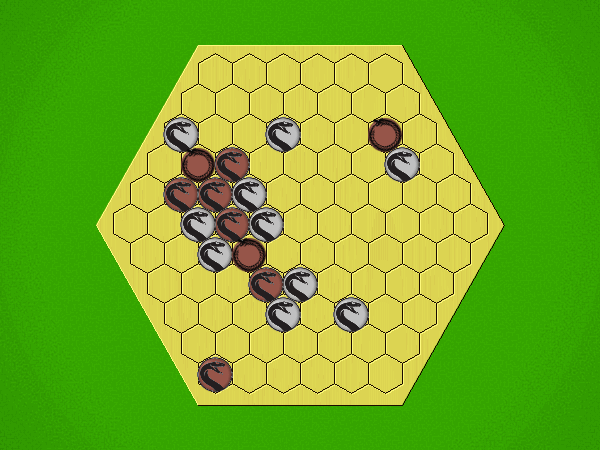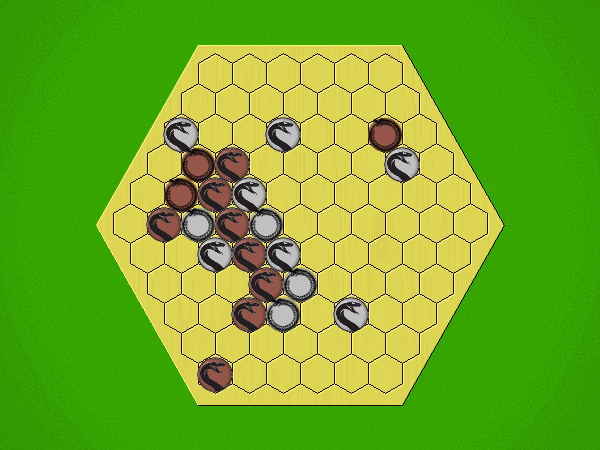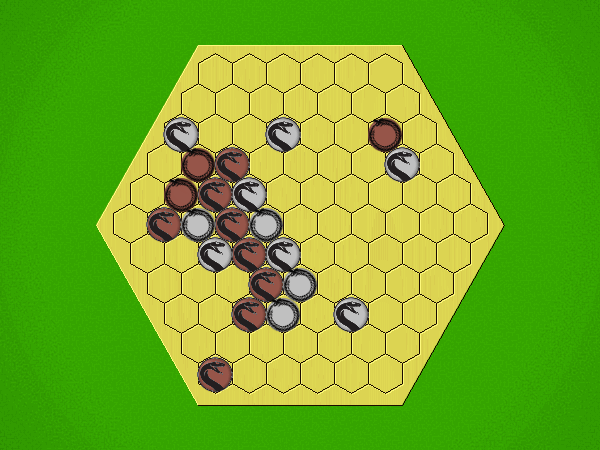
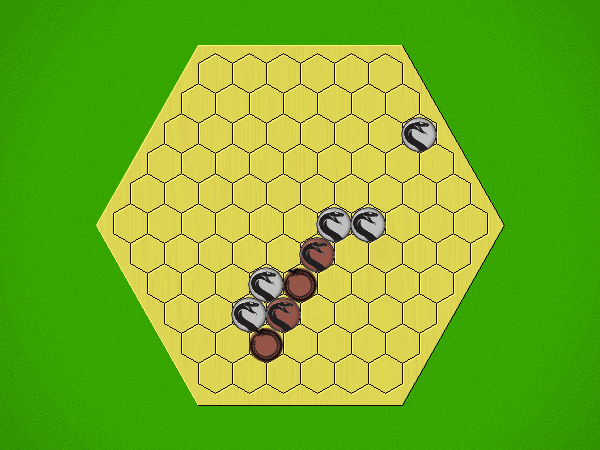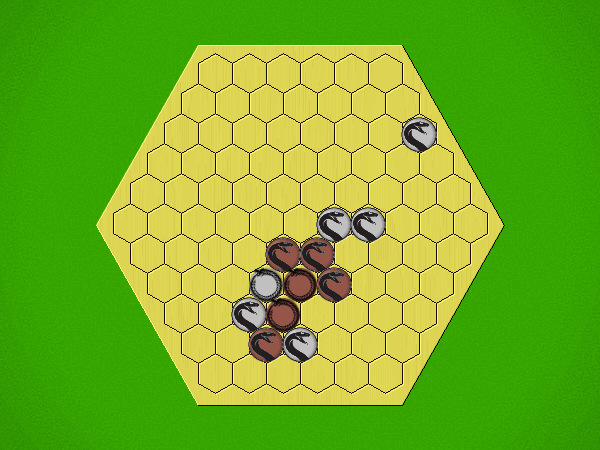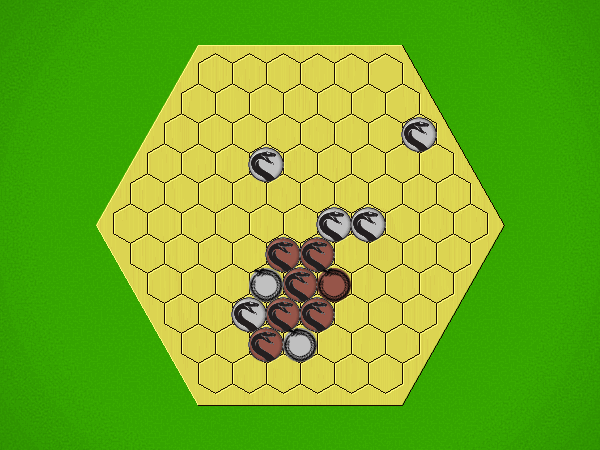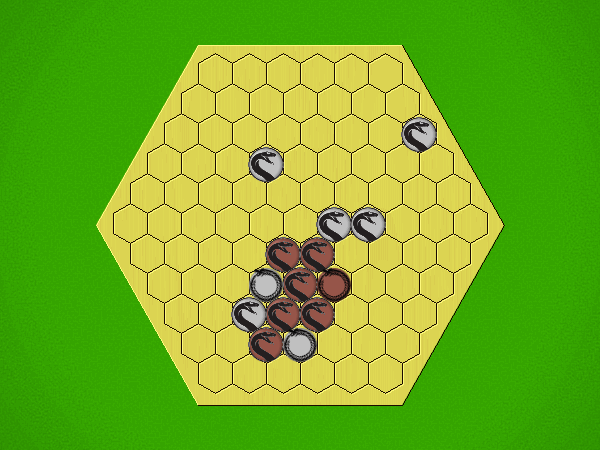
Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!

Equipment

A size 6 HexHex board
Enough Silver and Copper coins to cover the board (equal quantities of each)

Play

Each turn, starting with Silver, place a coin in an empty space with Heads showing; then flip all adjacent coins to their opposite sides.

Goal

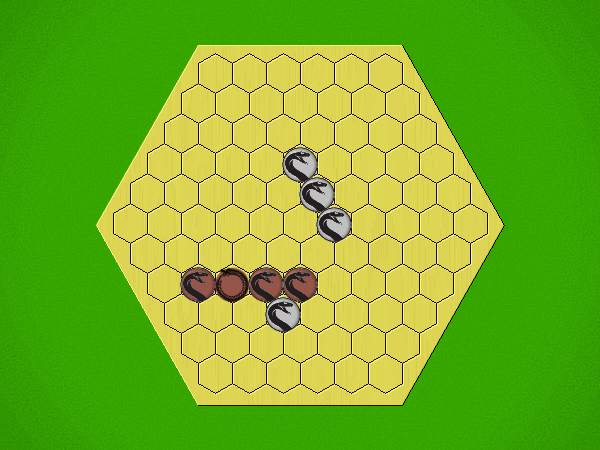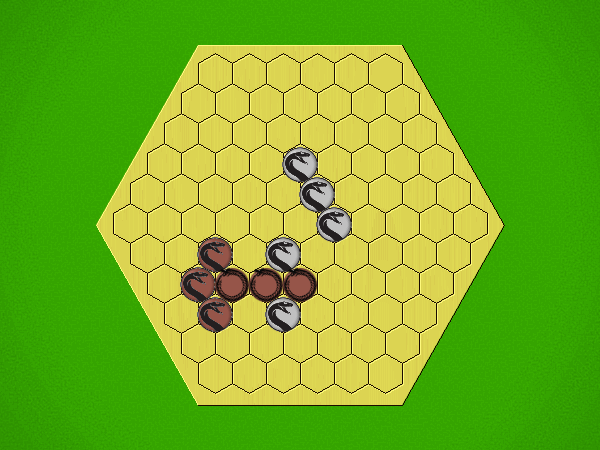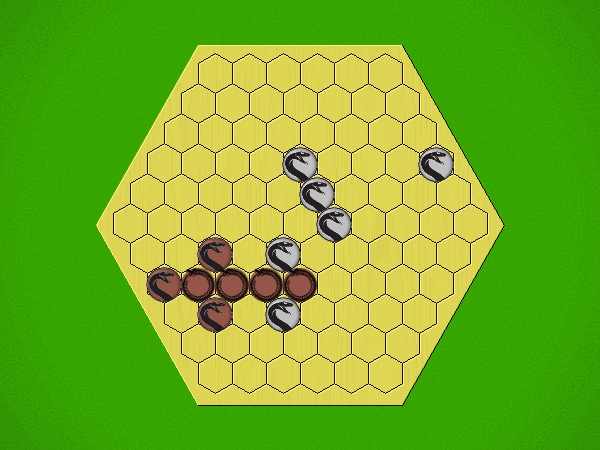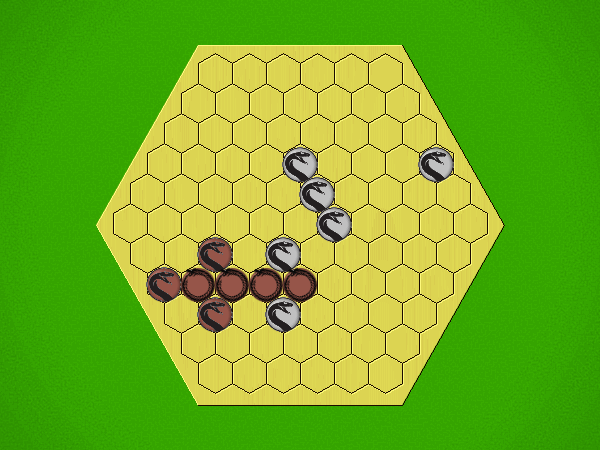
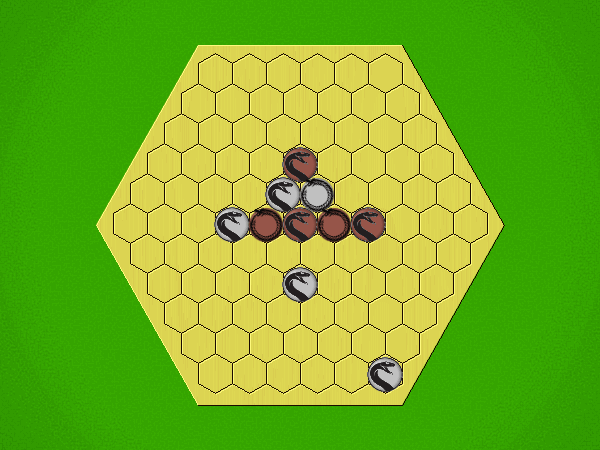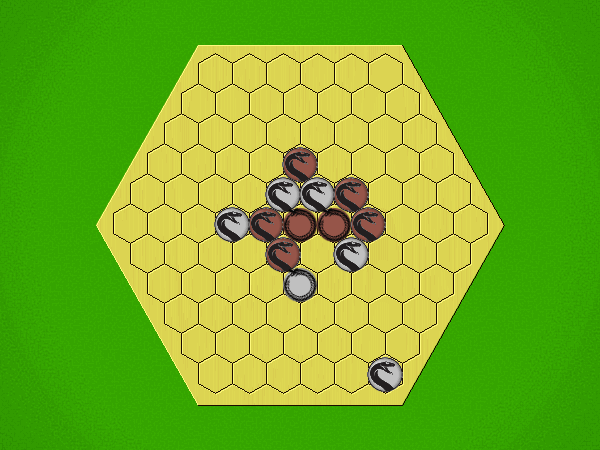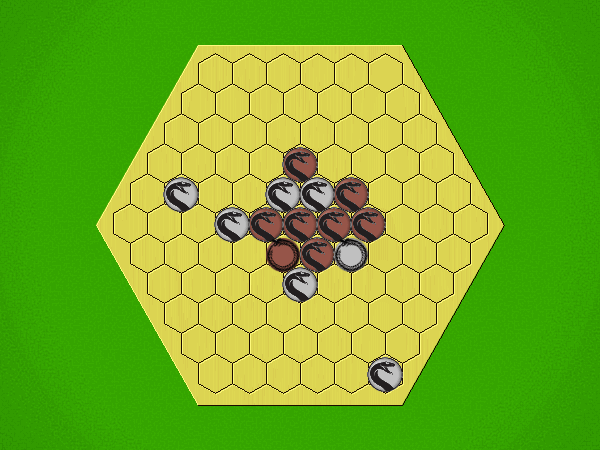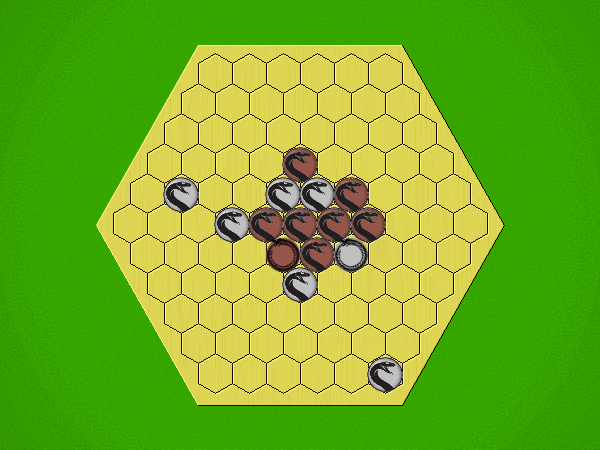
If, at the end of your turn, you have:

four of your pieces
in a contiguous straight line
showing the same side (all heads or all tails)

... then you win.

If the board is full and no one has won then the game is a draw.

Swap rule

To offset any first player advantage, play with the following swap rule:

First turn: Player 1 places a Silver piece
Second turn: Player 2 may play a Bronze piece or swap sides.

Simulations in Ai Ai suggest that the spaces 1 away from the edge are good swap candidates.

            x   x   x   x   x   x
          x   ?   ?   ?   ?   ?   x
        x   ?   s   s   s   s   ?   x
      x   ?   s   s   s   s   s   ?   x
    x   ?   s   s   s   s   s   s   ?   x
  x   ?   s   s   s   s   s   s   s   ?   x
    x   ?   s   s   s   s   s   s   ?   x
      x   ?   s   s   s   s   s   ?   x
        x   ?   s   s   s   s   ?   x
          x   ?   ?   ?   ?   ?   x
            x   x   x   x   x   x

s=swap, x=don't swap, ?=balanced

Miscellaneous

General comments:

Play: Combinatorial

Family: Combinatorial 2020

Mechanism(s): Capture,Movement,Race,Stacking

BGG Stats

BGG Entry	Flipping
BGG Rating	null
#Voters	null
SD	null
BGG Weight	null
#Voters	null
Year	null

Kolomogorov Complexity Analysis

Size (bytes)	27112
Reference Size	10915
Ratio	2.48

Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.

Playout Complexity Estimate

Playouts per second	28259.13 (35.39µs/playout)
Reference Size	917599.56 (1.09µs/playout)
Ratio (low is good)	32.47

Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.

State Space Complexity

% new positions/bucket

State Space Complexity	2442133639
State Space Complexity bounds	115077731 < 2442133639 < ∞
State Space Complexity (log 10)	9.39
State Space Complexity bounds (log 10)	8.06 <= 9.39 <= ∞
Samples	1106111
Confidence	0.00	0: totally unreliable, 100: perfect

State space complexity (where present) is an estimate of the number of distinct game tree reachable through actual play. Over a series of random games, Ai Ai checks each position to see if it is new, or a repeat of a previous position and keeps a total for each game. As the number of games increase, the quantity of new positions seen per game decreases. These games are then partitioned into a number of buckets, and if certain conditions are met, Ai Ai treats the number in each bucket as the start of a strictly decreasing geometric sequence and sums it to estimate the total state space. The accuracy is calculated as 1-[end bucket count]/[starting bucklet count]

Playout/Search Speed

Label	Its/s	SD	Nodes/s	SD	Game length	SD
Random playout	80,840	433	4,748,069	24,704	59	14
search.UCT	NaN	NaN			0	0

Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.

Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.

Mirroring Strategies

Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.

Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.

Win % By Player (Bias)

1: Silver win %	39.58±2.86	Includes draws = 50%
2: Gold win %	60.42±2.93	Includes draws = 50%
Draw %	6.58	Percentage of games where all players draw.
Decisive %	93.42	Percentage of games with a single winner.
Samples	1094	Quantity of logged games played

Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)

Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.

UCT Skill Chains

Match	AI	Strong Wins	Draws	Strong Losses	#Games	Strong Score	p1 Win%	Draw%	p2 Win%	Game Length
0	Random
2	UCT (its=3)	630	1	340	971	0.6188 <= 0.6493 <= 0.6787	49.54	0.10	50.36	56.26
32	UCT (its=33)	631	0	361	992	0.6057 <= 0.6361 <= 0.6655	52.32	0.00	47.68	53.17
45	UCT (its=46)	631	0	359	990	0.6069 <= 0.6374 <= 0.6667	48.08	0.00	51.92	51.01
57	UCT (its=58)	631	0	357	988	0.6082 <= 0.6387 <= 0.6680	50.71	0.00	49.29	48.63
69	UCT (its=70)	631	0	357	988	0.6082 <= 0.6387 <= 0.6680	49.09	0.00	50.91	45.62
82	UCT (its=83)	631	0	369	1000	0.6006 <= 0.6310 <= 0.6604	50.30	0.00	49.70	41.60
91	UCT (its=247)	631	0	174	805	0.7541 <= 0.7839 <= 0.8109	47.70	0.00	52.30	32.28
92	UCT (its=672)	631	0	200	831	0.7291 <= 0.7593 <= 0.7872	52.11	0.00	47.89	23.71
93	UCT (its=1828)	631	0	201	832	0.7282 <= 0.7584 <= 0.7863	53.00	0.00	47.00	18.93
94	UCT (its=4968)	631	0	178	809	0.7501 <= 0.7800 <= 0.8072	54.14	0.00	45.86	15.88
95	UCT (its=13506)	631	0	161	792	0.7673 <= 0.7967 <= 0.8233	53.16	0.00	46.84	14.71
96	UCT (its=13506)	497	0	503	1000	0.4661 <= 0.4970 <= 0.5279	52.70	0.00	47.30	15.92

Search for levels ended: time limit reached.

Level of Play: Strong beats Weak 60% of the time (lower bound with 95% confidence).

Draw%, p1 win% and game length may give some indication of trends as AI strength increases.

1st Player Win Ratios by Playing Strength

This chart shows the win(green)/draw(black)/loss(red) percentages, as UCT play strength increases. Note that for most games, the top playing strength show here will be distinctly below human standard.

Complexity

Game length	21.04
Branching factor	81.35
Complexity	10^39.85	Based on game length and branching factor
Samples	1094	Quantity of logged games played

Computational complexity (where present) is an estimate of the game tree reachable through actual play. For each game in turn, Ai Ai marks the positions reached in a hashtable, then counts the number of new moves added to the table. Once all moves are applied, it treats this sequence as a geometric progression and calculates the sum as n-> infinity.

Move Classification

Board Size	91	Quantity of distinct board cells
Distinct actions	92	Quantity of distinct moves (e.g. "e4") regardless of position in game tree
Good moves	42	A good move is selected by the AI more than the average
Bad moves	50	A bad move is selected by the AI less than the average
Response distance%	34.63%	Distance from move to response / maximum board distance; a low value suggests a game is tactical rather than strategic.
Samples	1094	Quantity of logged games played

Board Coverage

A mean of 22.73% of board locations were used per game.

Colour and size show the frequency of visits.

Game Length

Game length frequencies.

Mean	21.04
Mode	[16]
Median	18.0

Actions/turn

Table: branching factor per turn, based on a single representative* game. (* Representative in the sense that it is close to the mean game length.)

Action Types per Turn

This chart is based on a single representative* game, and gives a feel for the types of moves available throughout that game. (* Representative in the sense that it is close to the mean game length.)

Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.

Swap Heatmap (Full Scan)

Colour shows the frequency of swaps on turn 2 if this move is played on turn 1; black < red < yellow < white.

Based on 100 trials/move at 0.1s thinking time each.

Openings

Moves	Animation
i3,k2,j2,g4,j3,h3,k1,i2,k3,c4
i3,h3,j2,g4,f4,k2,k1,f1,k4,e5
i3,g4,j3,h3,f4,k2,k4,e5,k3,c4
k3,a8,d4,j5,k4,i5,h5,j4,f6,j3
d4,a8,k3,j5,k4,i5,h5,j4,f6,j3
i3,k2,j2,g4,j3,h3,k1,i2,k3
i3,h3,j2,g4,f4,k2,k1,f1,k4
i3,g4,j3,h3,f4,k2,k3,c4,k4
i3,g4,j3,h3,f4,k2,k4,e5,k3
k3,a8,d4,j5,k4,i5,h5,j4,f6
d4,a8,k3,j5,k4,i5,h5,j4,f6
b5,d10,j5,i6,h7,a6,f7,k5,b6

Opening Heatmap

Colour shows the success ratio of this play over the first 10moves; black < red < yellow < white.

Size shows the frequency this move is played.

Swap Heatmap (Historic)

Colour shows the frequency of swaps on turn 2 if this move is played on turn 1; black < red < yellow < white.

Size shows the frequency this move is played.

Unique Positions Reachable at Depth

0	1	2	3	4
1	91	8372	441866	22504616

Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.

Shortest Game(s)

No solutions found to depth 4.

Puzzles

Puzzle	Solution
Black to win in 7 moves
Black to win in 7 moves
White to win in 7 moves
Black to win in 7 moves
Black to win in 7 moves
Black to win in 5 moves
Black to win in 5 moves
Black to win in 5 moves
Black to win in 5 moves
Black to win in 5 moves
Black to win in 5 moves
Black to win in 5 moves

Selection criteria: first move must be unique, and not forced to avoid losing. Beyond that, Puzzles will be rated by the product of [total move]/[best moves] at each step, and the best puzzles selected.