Change in Material Per Turn
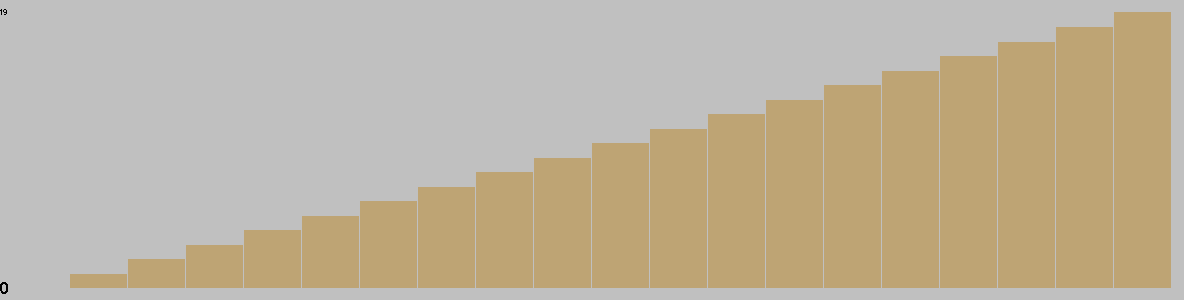
This chart is based on a single playout, and gives a feel for the change in material over the course of a game.
Add pieces to the board, stop your opponent from moving
The game is played in a virtual 9x9 grid according to the constraints, until one player cannot play. The last player to place a piece wins.
There are four constraints:
General comments:
Play: Combinatorial
Family: Combinatorial 2012,Combinatorial 2013
Mechanism(s): Stalemate,Tile
| BGG Entry | Four |
|---|---|
| BGG Rating | 7.85185 |
| #Voters | 27 |
| SD | 1.1849 |
| BGG Weight | 1.5 |
| #Voters | 2 |
| Year | 2012 |
| User | Rating | Comment |
|---|---|---|
| hippiephysicschick | N/A | made pnp copy from blokus pieces |
| donaldrnelson | N/A | W |
| mrraow | 10 | My game :) The four colour theorem is one of those iconic maths problems; it's easy to state ("any 2d map can be coloured with at most four colours, so that no two adjacent countries are the same colour"), and a nightmare to prove. In fact, last time I looked, the proof had so many special cases that a computer was required to check it. It also sounds like a game already - "here's a sheet of paper, colour it in..."; and, I confess, I have been playing around with it since the 1980's. Aside: for those who like the sound of a four-colour colouring puzzle, look here: http://www.nikoli.com/en/take_a_break/four_color_problem/ ANYhow, the simplest game using the mechanism I can imagine is "Players alternate turns placing pieces, so no two pieces of the same colour touch. Last person to play wins." Unfortunately, there are a couple of problems here. The first is that early moves are likely to be unimportant; that is, players can't make meaningful decisions at the start of the game. The second is that late decisions are too constrained by early moves, i.e. the end of the game is a series of forced moves. Combine the two, and players can go from "I don't know what I'm doing" to "I've lost" in a single move; which is frustrating, to say the least. I kicked the idea around with Cameron Browne for a while, and Chroma was born - here, we solved the problems with two things; first, the 3D board means that not all board spaces are accessible at the start of the game, which makes early moves less opaque; secondly, the colours are played in a fixed sequence, which allows players to look ahead and deliberately block the opponent. Chroma isn't perfect, though... while very beautiful, it's a little sad that games will often end when the board is only half full. Anyway, fast forwards a couple of years, and I changed computers; in the process, I transferred some old documents from my previous computers, and found a file from 1994 containing some tiles from a previous attempt at a 4-colour game which I had completely forgotten. The tiles were each made of several coloured hexagons stuck together, so bear very little resemblance to Four as it is today; but the idea of different shapes in each colour was the starting point. After that came the name, which in turn led to the idea of having exactly four shapes and four constraints. A lot of trial and error went into finding the four shapes that led to the most interesting game. ... and here it is. Not all the blocks will be played before someone can't move, so while getting rid of the larger pieces early can be an advantage, being flexible in terms of playable piece types and colours is more so. That means players can make intuitive moves at the start of the game when they have lots of freedom (get rid of/reserve space for your 3- and 4- pieces early), yet can profitably think hard in the end game. |
| boardgamebird97 | 9 | |
| andres0804 | 10 | |
| clark94 | 9 | Suprisingly fun and a suprising brain burner. With not alot of possible moves play goes quickly. A fun game to do best 2 out of 3 or best 3 out of 5. |
| fogus | 6 | In the family of Nim-likes where the last player able to place a piece wins. The pieces have two features (shape and color) and the placement restrictions add enough to the game to allow depth without too much fuss. Quick and easy to get started. |
| Rakasis | 7.5 | ~ |
| van00uber | 6 | |
| pleclenuesse | 7 | |
| darrylsroy | 7 | DIY magnetic version |
| russ | 7 | Good placement game! When learning, it can be easy to forget about the restriction that you can't place the color or size which the opponent just placed. It's somehow easier to remember that you can't place adjacent to the same color or size (since you directly see the mistake if you do it). :) |
| ceenan | 7 | |
| emike | 9 | Elegant and fun. |
| Arcanio | 7 | |
| zefquaavius | 9 | Constraints like crazy from simple rules, permitting some very interesting strategy and such. |
| camb | 8 | Nice elegant game. |
| nestorgames | 9 | |
| leyton | 8.5 | Disclaimer - I do know the designer. On first appearances the game appears to be a muscular and aggressive abstract. You are directly in conflict with your opponent from the first move and the 4 rules especially the virtual grid give a sense of toe to toe combat with nowhere to run. However, I think there is more to it than an abstract 'cage fight' with each player trying to get the upper hand. I would like to explore the various openings. The tactic of geting your two by two squares onto the board early (which for me was a clear tactic at the start) may leave you tied up in the endgame and with practice a player can respond cleverly to the opponents large pieces arriving on the table early. I think Four in terms of clarity of idea, simplicity of ruleset and the combative nature (I do not mind a bit of a fight) makes this game my favourite abstract design of Stephens. I would like to explore it more and see where subtleties can be found in contrast to the big knockout punches but I think this game has real potential. |
| zeder | 6 | |
| Jedrique | 8 | |
| gabriel_k | N/A | PNP |
| jejo | 7 | Lego |
| Jugular | 8 | |
| Helmi68 | 7 | |
| Takvorian | 9 | A very clever tile laying game. Easy rules, but you have to concentrate quite a bit to win. Together with Zaic this is my favorite tile laying game. |
| grid | N/A | Adding this to the long list of Nestorgames I wish to own. |
| Josquin | 9 | |
| glanfam | 6 | |
| EllenM | 8 | Really good game - thinking through the placement options. Win condition of placing the last piece makes it better than if it was most placed (in which case 1st player has a clear advantage). The nestorgames edition pieces are nice. Keeping in the gets-regular-play part of the collection (ck . Benefit to being 1st or 2nd?) |
| jmastill | 8 |
| AI | Wins vs prev level | Draws | Losses | #Games | Win% |
|---|---|---|---|---|---|
| Random | |||||
| Grand Unified UCT(U1-T,rSel=s, secs=0.01) | 36 | 0 | 5 | 41 | 87.80 |
| Grand Unified UCT(U1-T,rSel=s, secs=0.03) | 36 | 0 | 14 | 50 | 72.00 |
| Grand Unified UCT(U1-T,rSel=s, secs=0.07) | 36 | 0 | 11 | 47 | 76.60 |
| Grand Unified UCT(U1-T,rSel=s, secs=0.20) | 36 | 0 | 8 | 44 | 81.82 |
| Grand Unified UCT(U1-T,rSel=s, secs=0.55) | 36 | 0 | 10 | 46 | 78.26 |
| Grand Unified UCT(U1-T,rSel=s, secs=4.03) | 36 | 0 | 9 | 45 | 80.00 |
Level of Play: strong beats weak 60% of the time (lower bound with 90% confidence).
| Size (bytes) | 31732 |
|---|---|
| Reference Size | 10328 |
| Ratio | 3.07 |
Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.
| Playouts per second | 2743.19 (364.54µs/playout) |
|---|---|
| Reference Size | 571297.99 (1.75µs/playout) |
| Ratio (low is good) | 208.26 |
Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.
| 1: Player 1 win % | 47.12±0.98 | Includes draws = 50% |
|---|---|---|
| 2: Player 2 win % | 52.88±0.98 | Includes draws = 50% |
| Draw % | 0.00 | Percentage of games where all players draw. |
| Decisive % | 100.00 | Percentage of games with a single winner. |
| Samples | 9990 | Quantity of logged games played |
Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)
Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.
Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.
Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.
| Game length | 21.97 | |
|---|---|---|
| Branching factor | 94.29 | |
| Complexity | 10^39.30 | Based on game length and branching factor |
| Samples | 9990 | Quantity of logged games played |
| Distinct actions | 3160 | Number of distinct moves (e.g. "e4") regardless of position in game tree |
|---|---|---|
| Good moves | 1189 | A good move is selected by the AI more than the average |
| Bad moves | 1971 | A bad move is selected by the AI less than the average |
| Samples | 9990 | Quantity of logged games played |

This chart is based on a single playout, and gives a feel for the change in material over the course of a game.
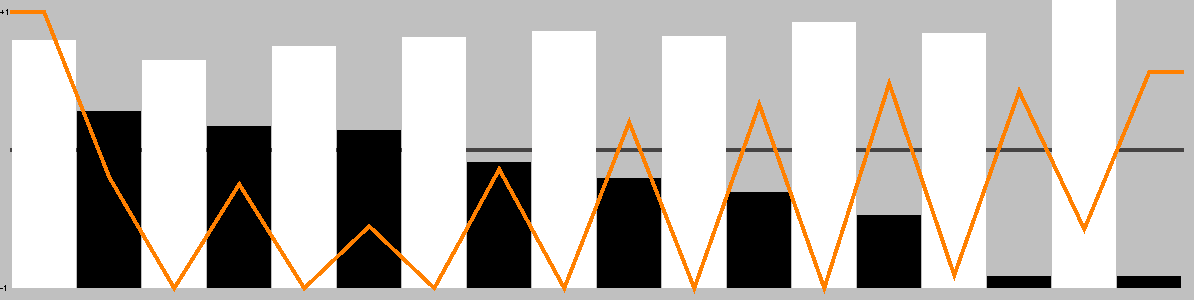
This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).
The lead changed on 33% of the game turns. Ai Ai found 0 critical turns (turns with only one good option).
Overall, this playout was 88.89% hot.

This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).
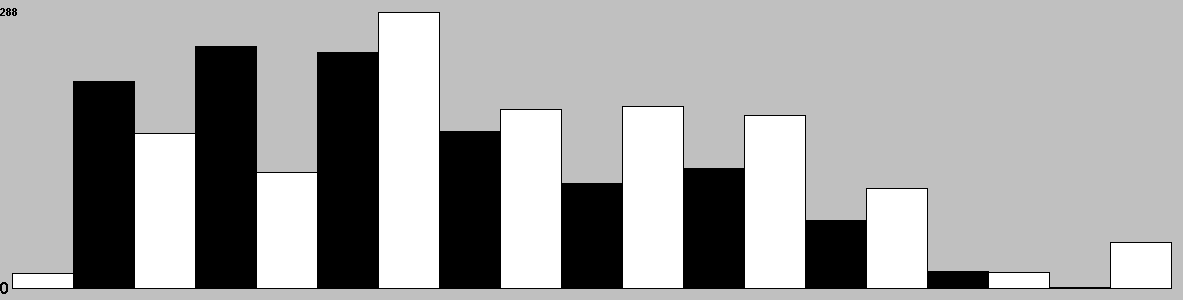
Table: branching factor per turn.
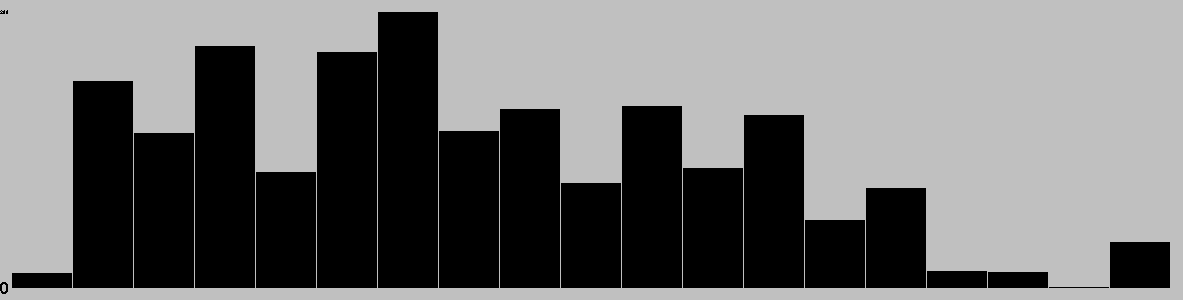
This chart is based on a single playout, and gives a feel for the types of moves available over the course of a game.
Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.
| 0 | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 16 | 2512 | 241672 |
Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.
No solutions found to depth 3.
| Moves | Animation |
|---|---|
| Green4BOX-c3,Red2V-b2,Blue3NE-a4,Green4BOX-a3,Yellow3SE-i3,Red4BOX-h1,Blue2H-i9 |  |
| Green4BOX-c3,Red2V-b2,Blue3NE-a4,Green4BOX-a3,Yellow3SE-i3,Red4BOX-h1 |  |
| Yellow4BOX-c3,Red3SE-e3,Green4BOX-g4,Blue3NW-b3,Red4BOX-d1,Yellow3SW-g3 |  |
| Red2H-c3,Green3SW-c5,Blue4BOX-b6,Yellow3NE-f1,Blue2H-f2 |  |
| Yellow2H-c3,Red4BOX-d4,Green3SW-d2,Blue4BOX-a3,Red3NW-b2 |  |
| Green4BOX-c3,Blue3NE-a4,Yellow1DOT-d3,Green4BOX-c6,Red3NW-f1 |  |
| Green4BOX-c3,Yellow1DOT-b3,Blue3NE-b4,Green4BOX-c6,Red3NW-f1 |  |
| Green4BOX-c3,Blue3SW-b4,Yellow4BOX-a4,Red3NW-b3,Blue4BOX-d1 |  |
| Green4BOX-c3,Blue3NE-b5,Red4BOX-b7,Yellow2V-g2,Blue1DOT-e9 | 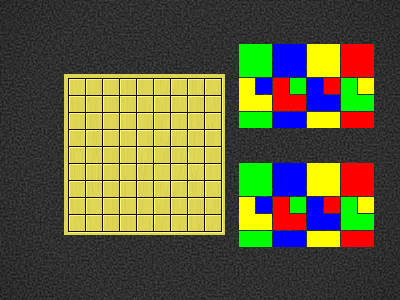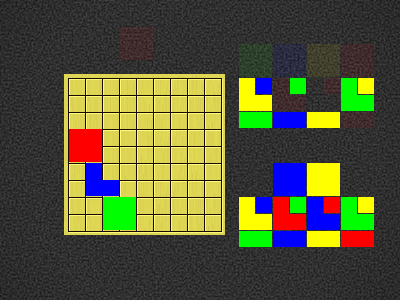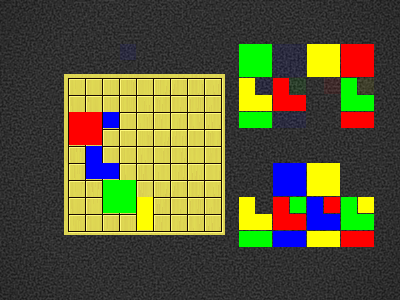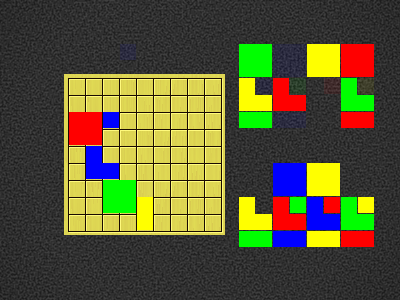 |
| Red4BOX-c3,Green3SE-c2,Yellow4BOX-b1,Red3SE-a4,Blue4BOX-h5 |  |
| Red4BOX-c3,Green3SW-f3,Yellow4BOX-g3,Red3NW-j4,Blue4BOX-j2 |  |
| Red4BOX-c3,Yellow3NW-f3,Green4BOX-g2,Yellow2V-i4,Blue3SE-h2 |  |
| Puzzle | Solution |
|---|---|
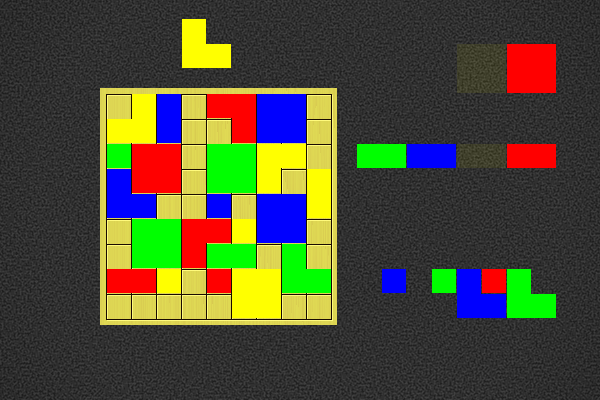 Player 2 to win in 5 moves | |
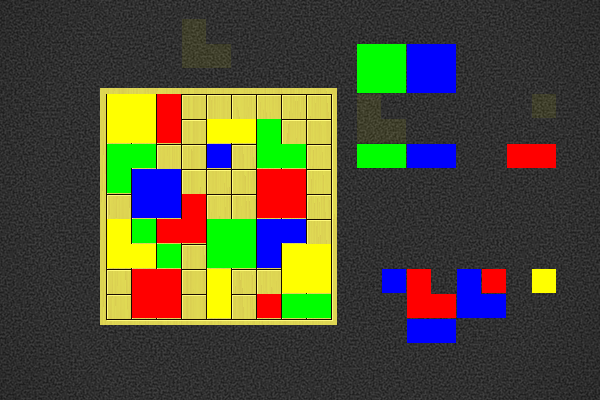 Player 2 to win in 5 moves | |
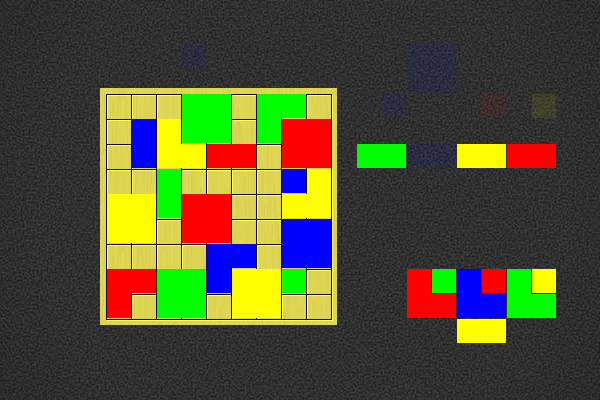 Player 2 to win in 5 moves | |
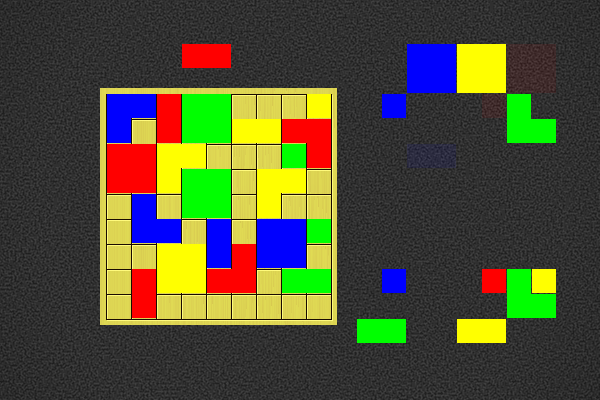 Player 2 to win in 3 moves | |
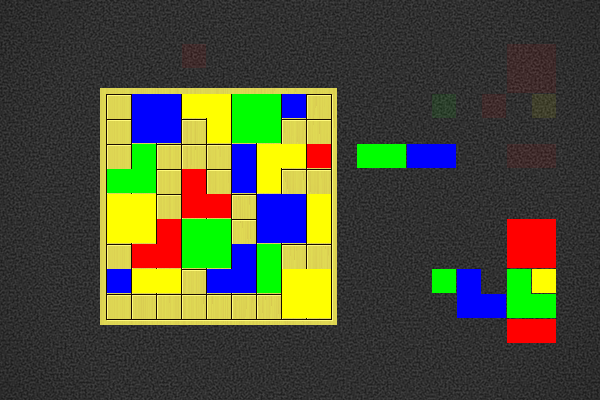 Player 2 to win in 5 moves |
Selection criteria: first move must be unique, and not forced to avoid losing. Beyond that, Puzzles will be rated by the product of [total move]/[best moves] at each step, and the best puzzles selected.