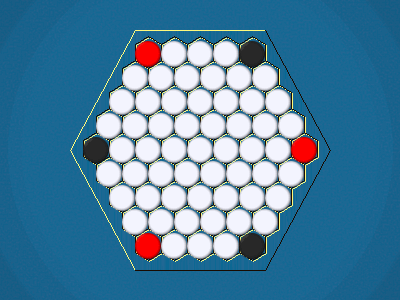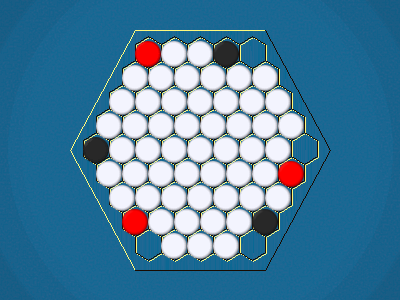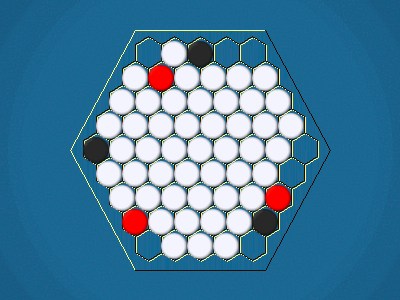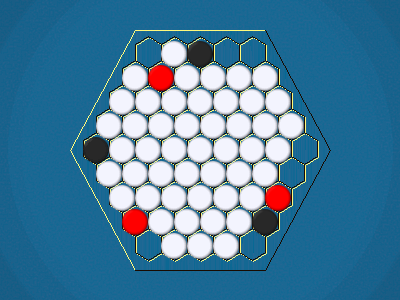
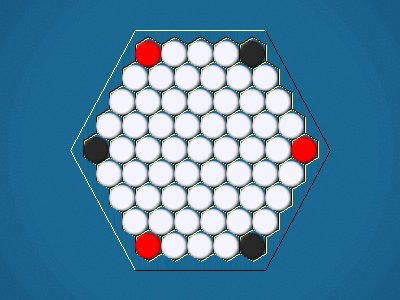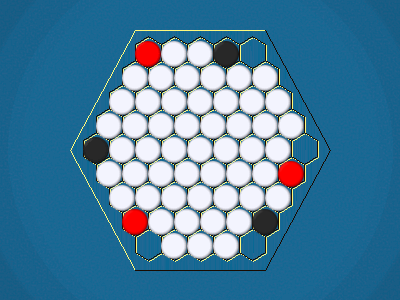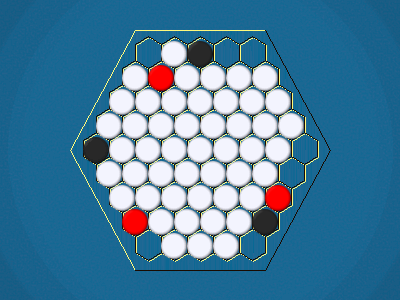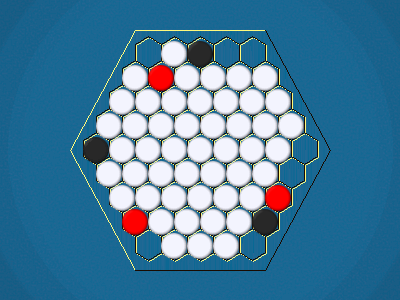
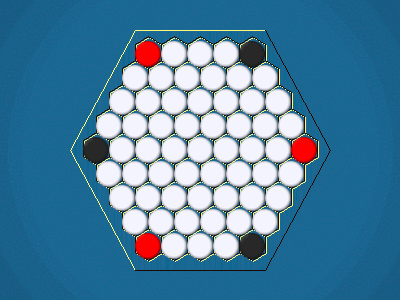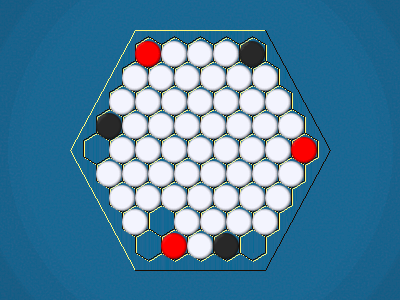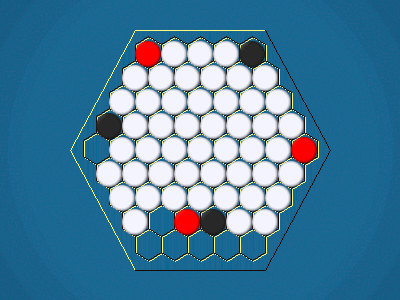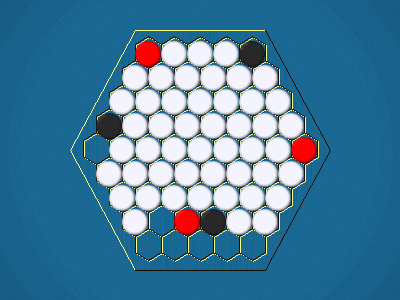
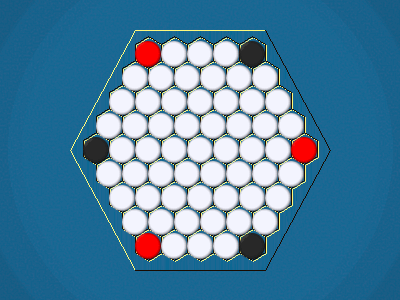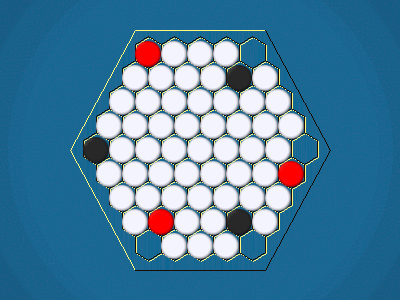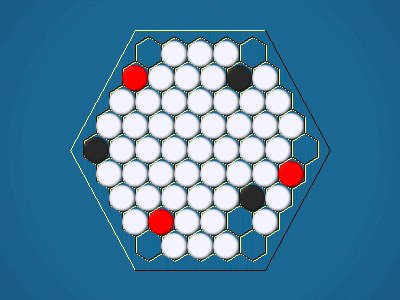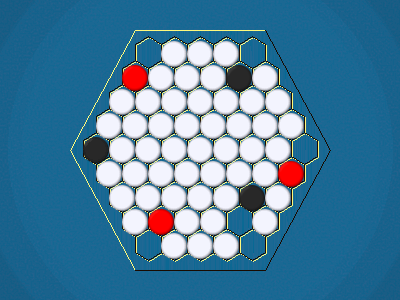
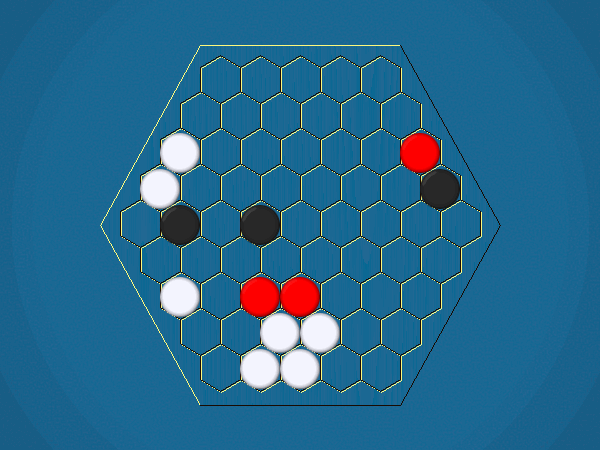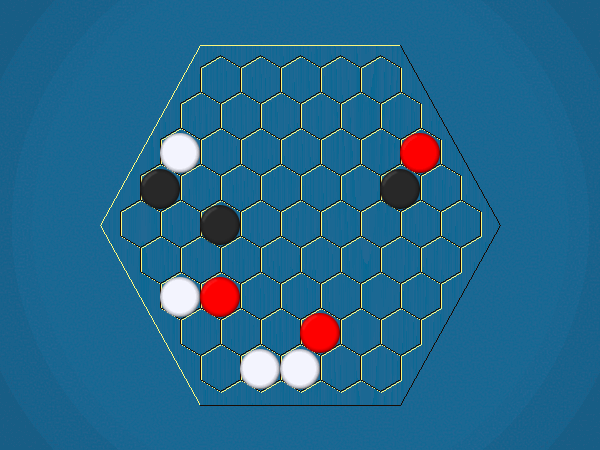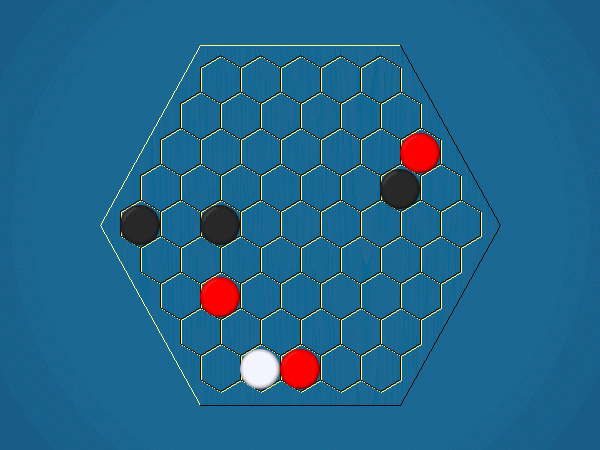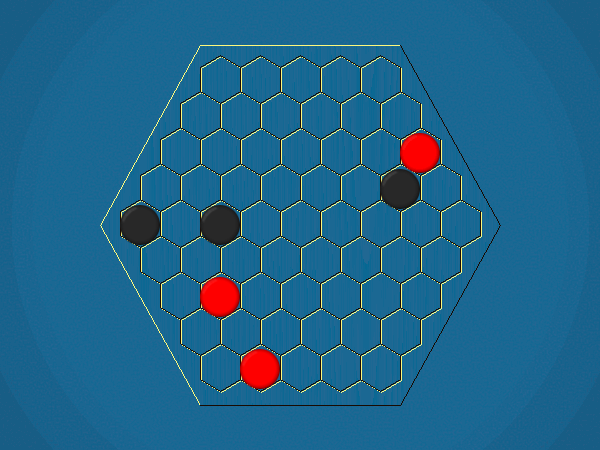
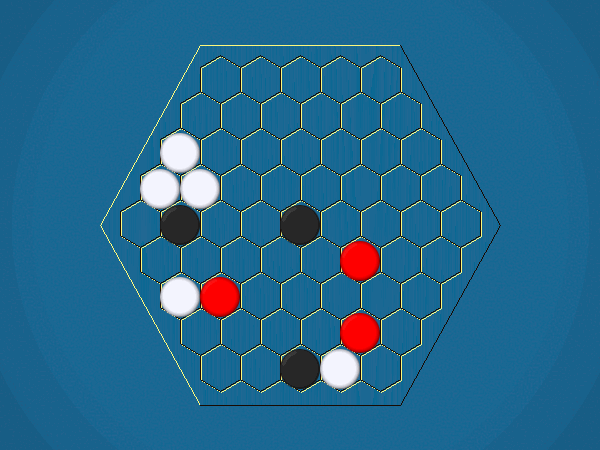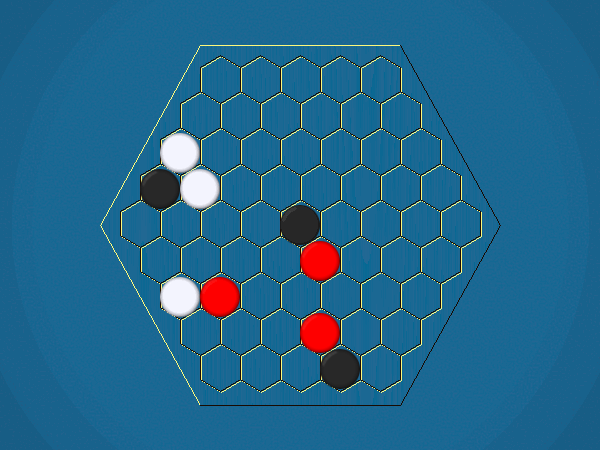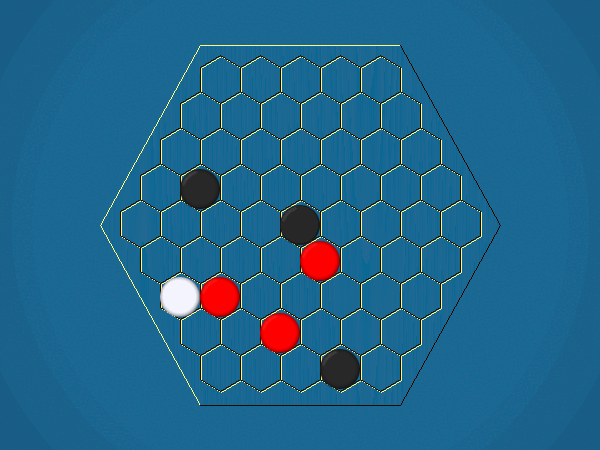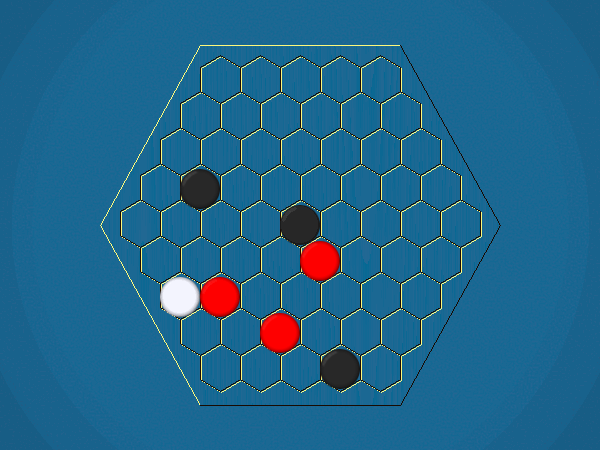
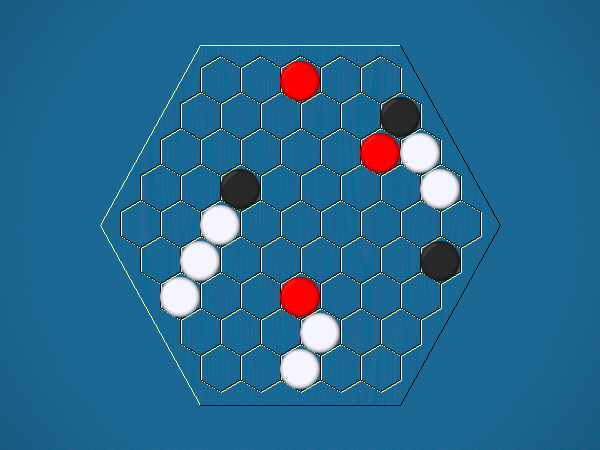
Full Report for Icebreaker by Mark Steere

Rules

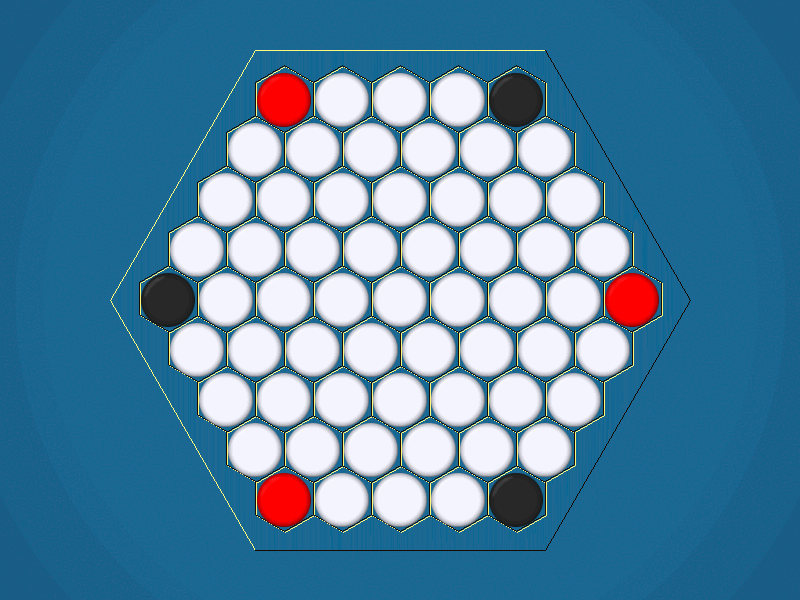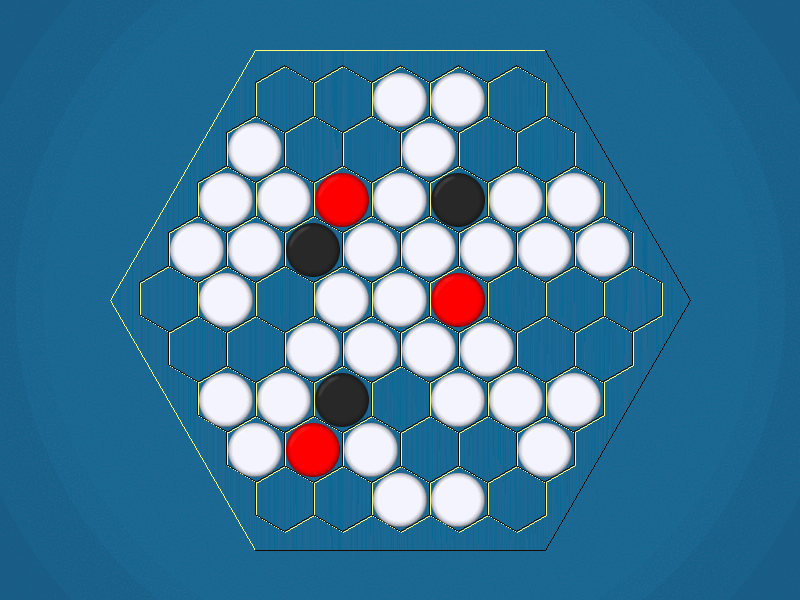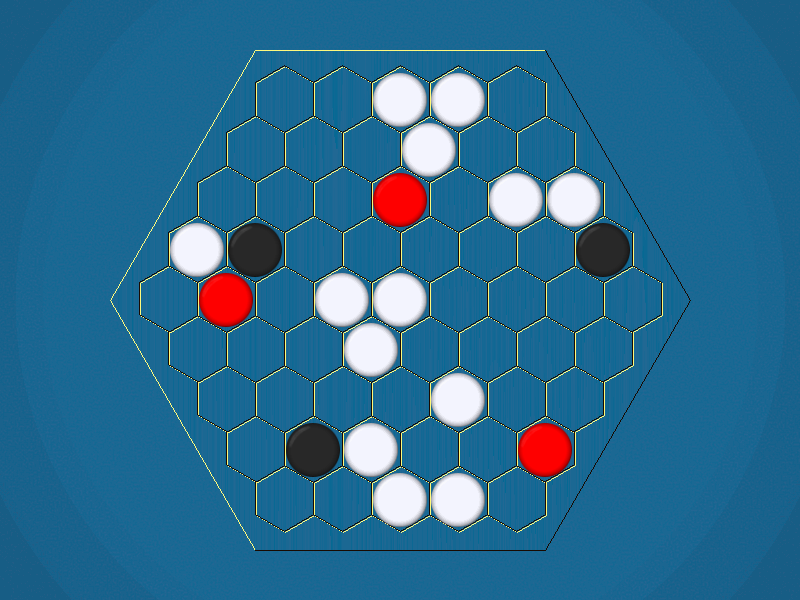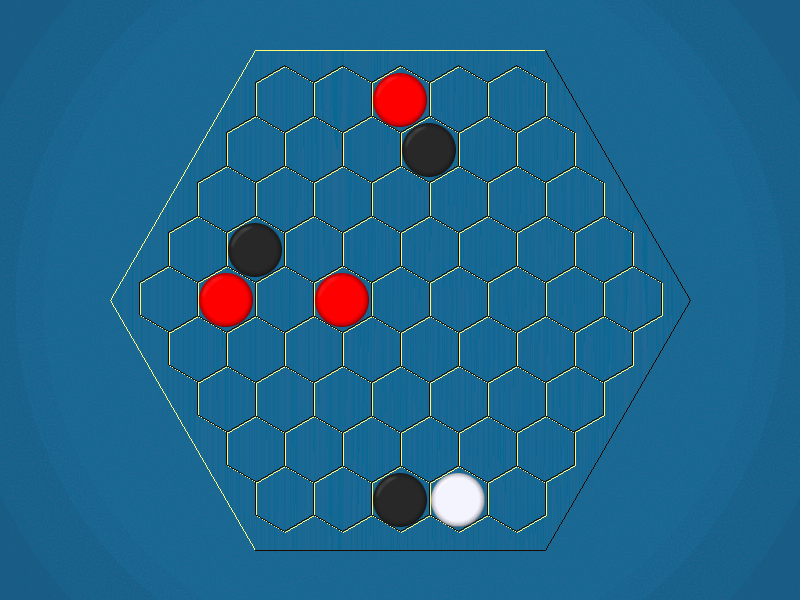
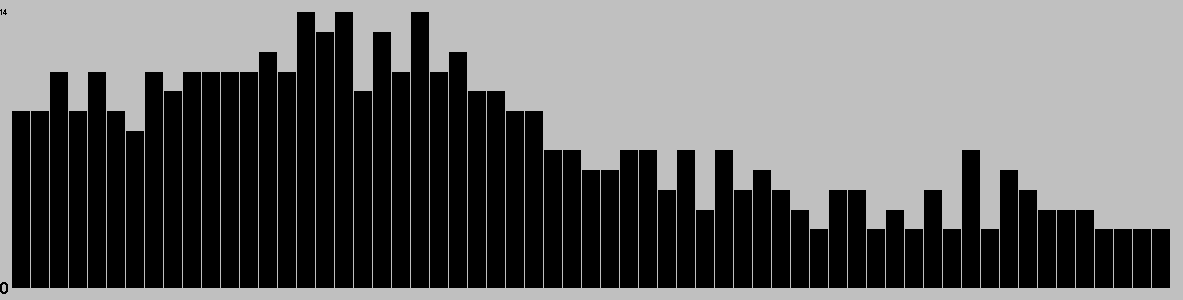
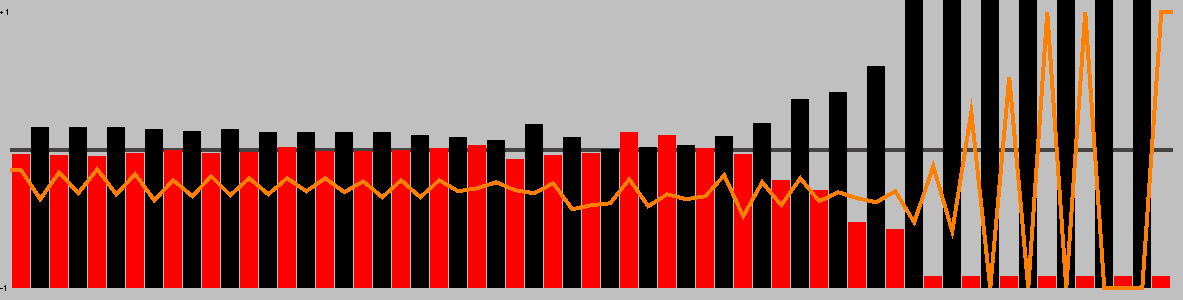
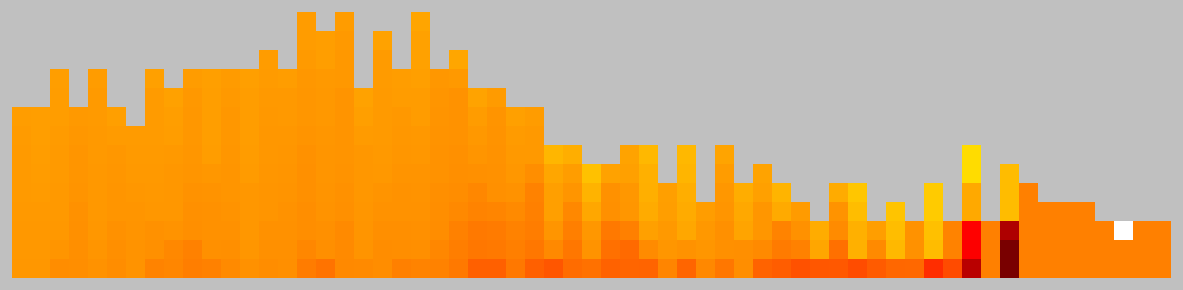
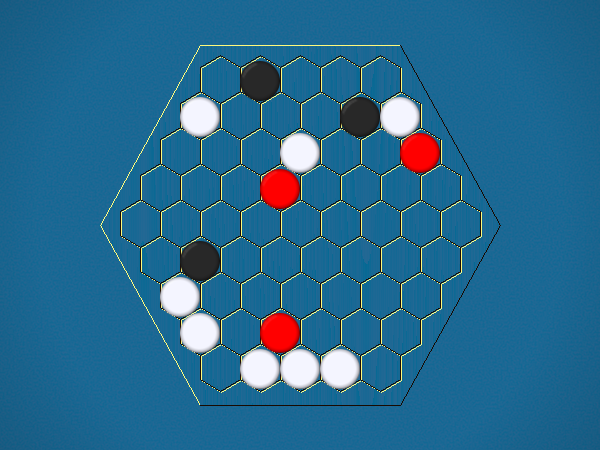
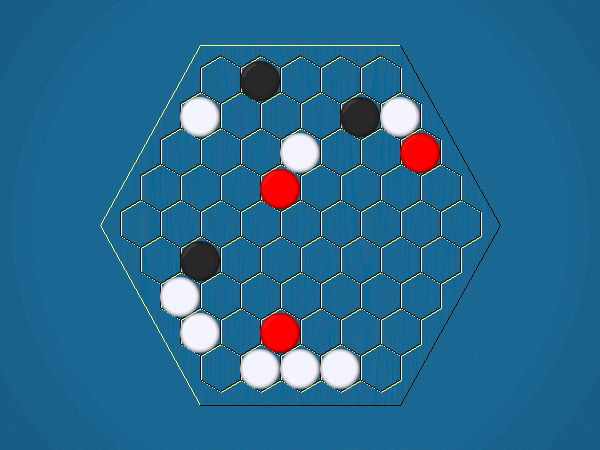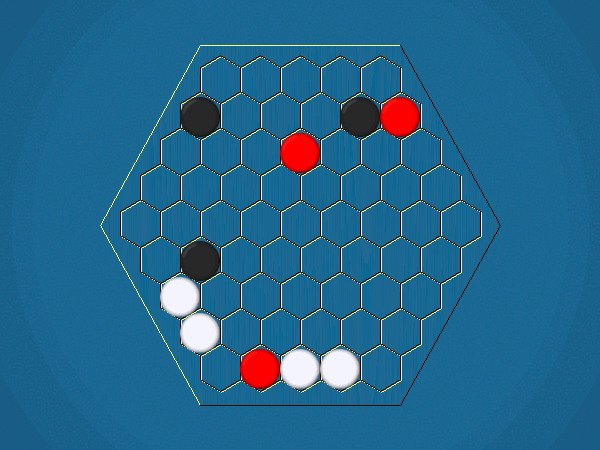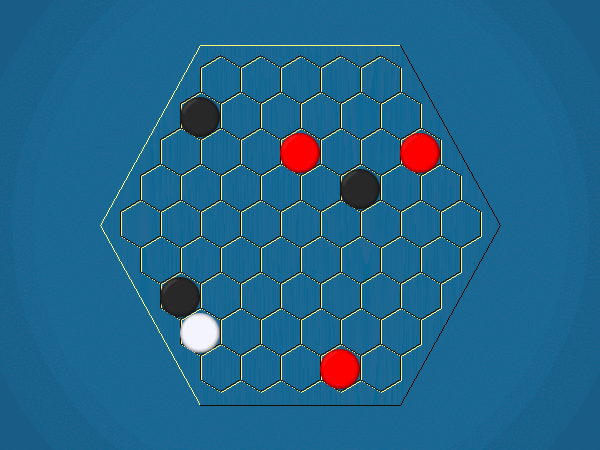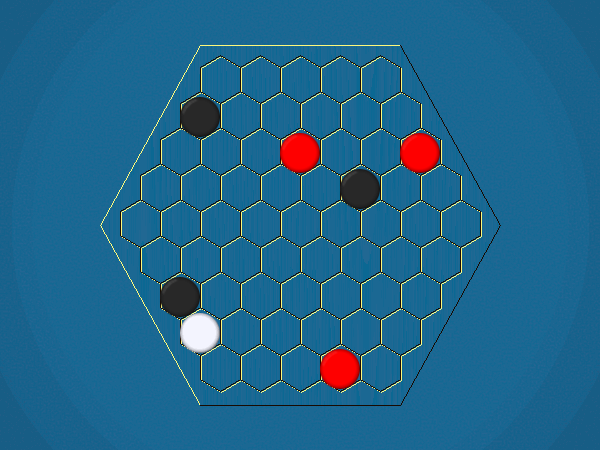
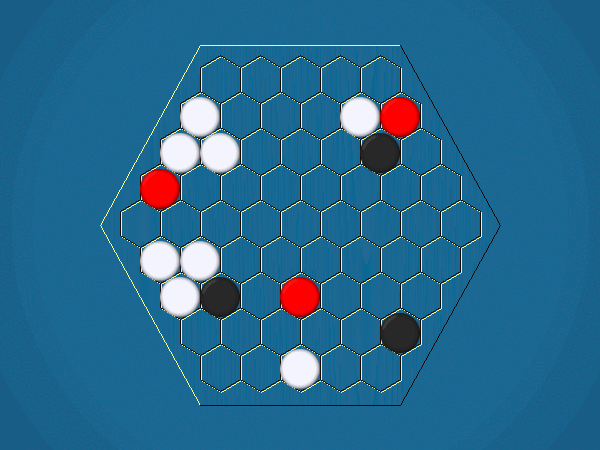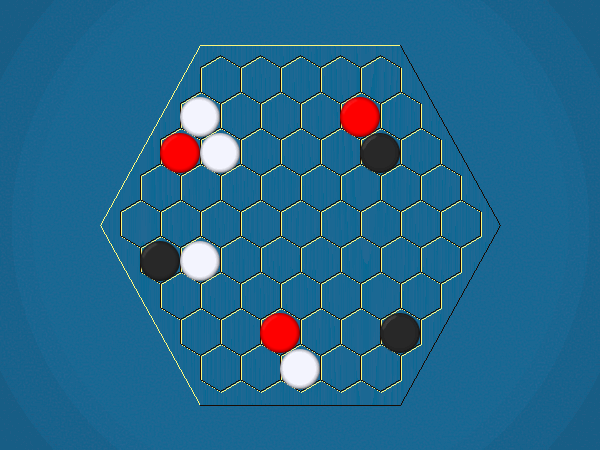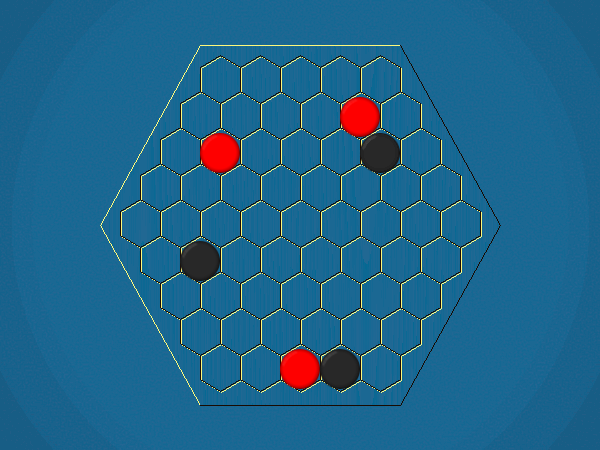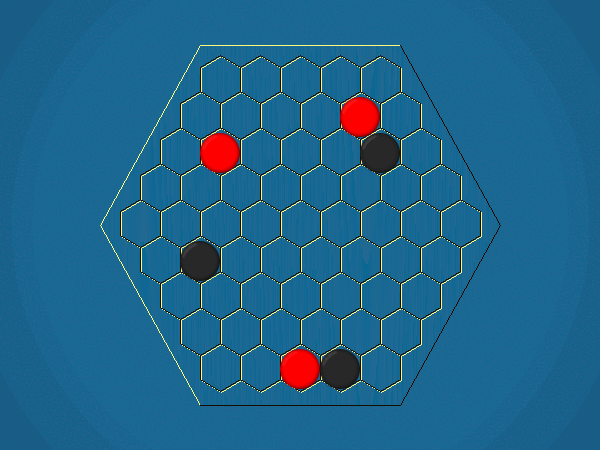
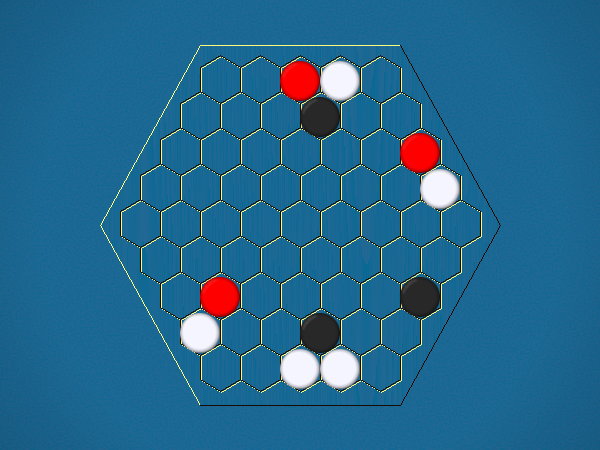
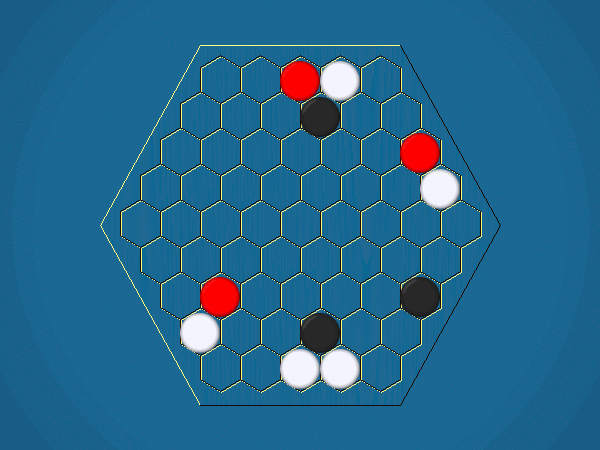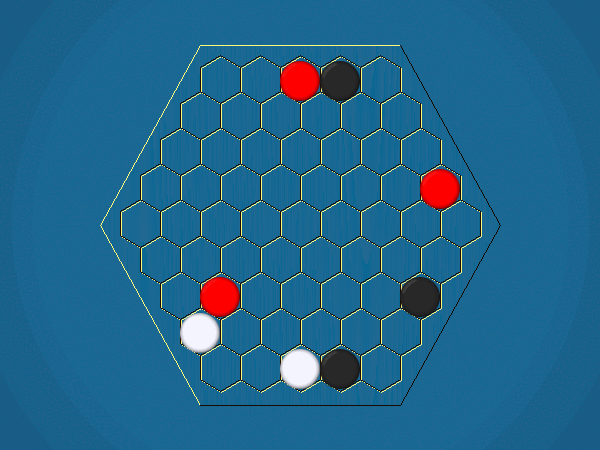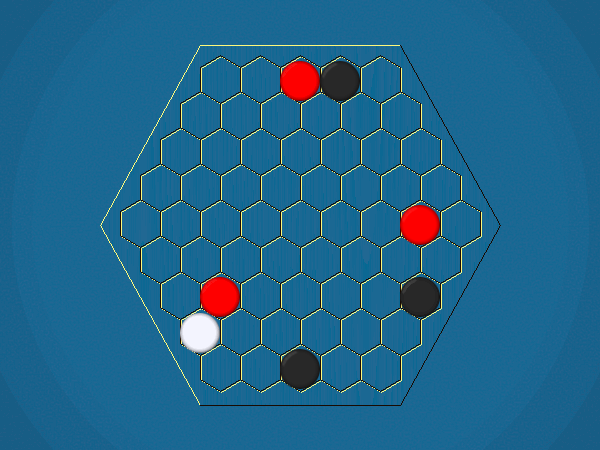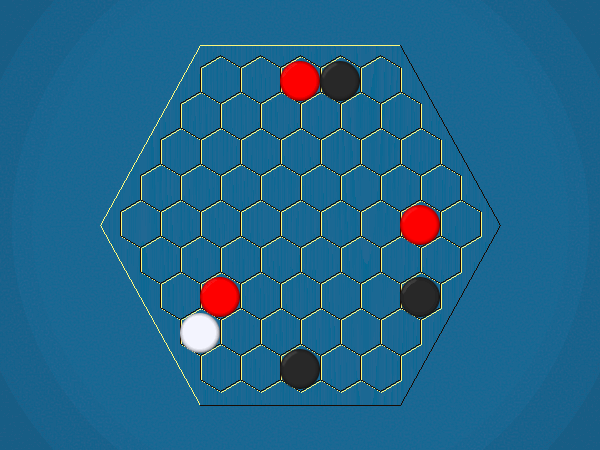
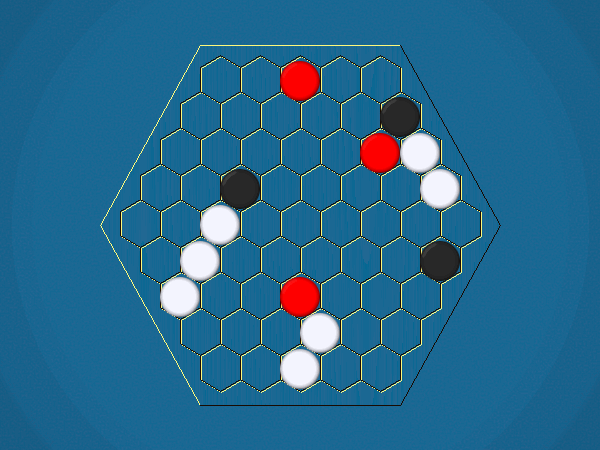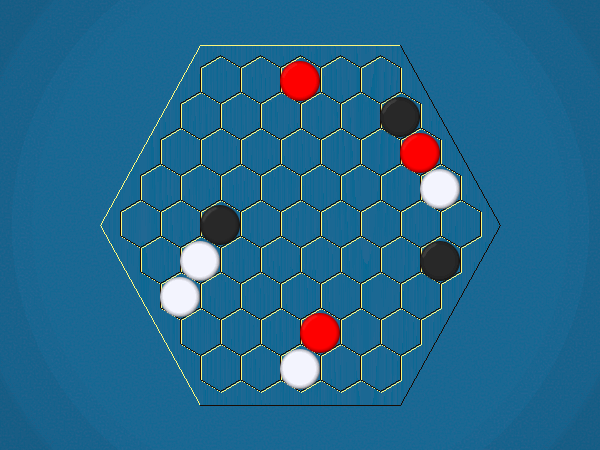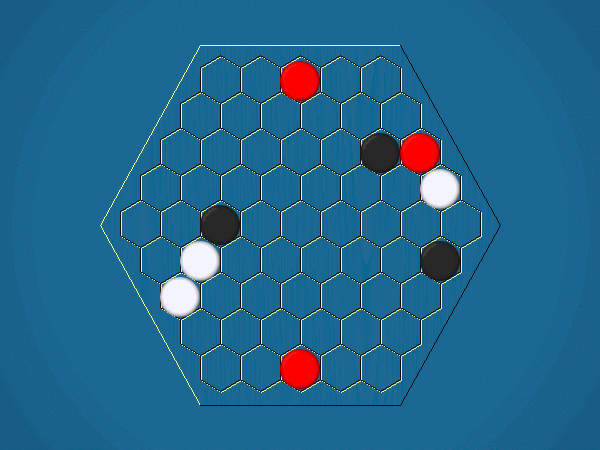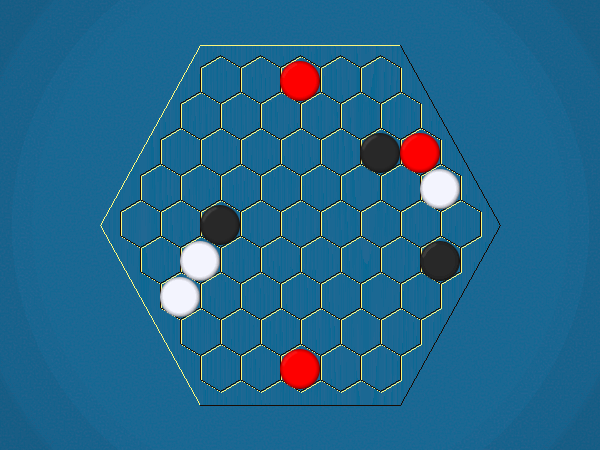
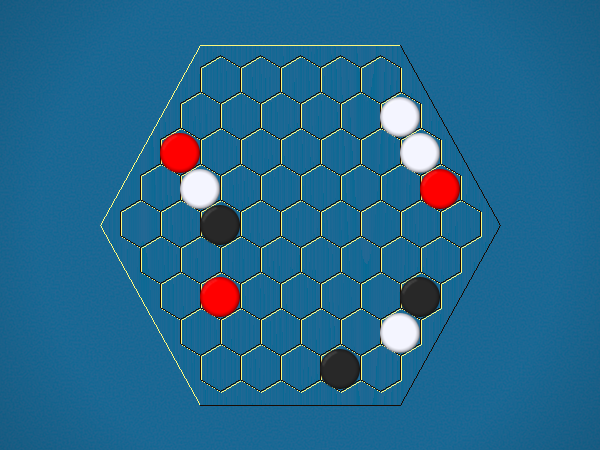
Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!

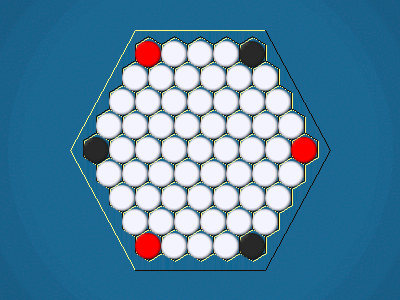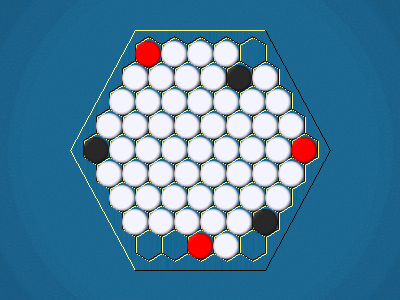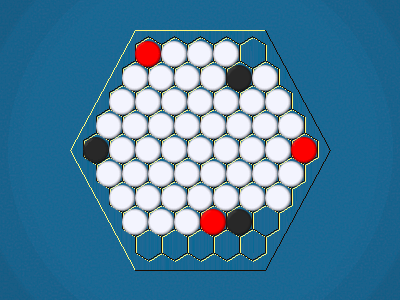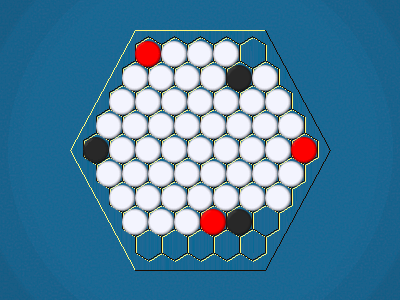
Full rules, including illustrations, are available at Mark Steere Games.

MOVES

You must move one of your ships to an adjacent cell which doesn't contain another ship. By moving to a cell containing an iceberg, you capture the iceberg, and your score increases by 1.

MOVE DIRECTION

You must select one of your ships to move, and move it closer to its closest iceberg. Distance is measured by the number of cells between ship and iceberg along the shortest path of cells that connects them, going around other ships. If the ship you've chosen to move has icebergs adjacent to it, you must capture one of them.>/p>

OBJECT OF THE GAME

The goal is to capture the majority of the icebergs. On a size 5 board, there are 55 icebergs starting out. If you capture 28 of them, youwin.

Miscellaneous

General comments:

Requires accurate responses to threats.

Play: Combinatorial

Mechanism(s): Capture,Scoring

BGG Stats

BGG Entry	Icebreaker
BGG Rating	5
#Voters	1
SD	0
BGG Weight	0
#Voters	0
Year	2021

BGG Ratings and Comments

User	Rating	Comment
OhmSweetOhm	5

Kolomogorov Complexity Analysis

Size (bytes)	27404
Reference Size	10673
Ratio	2.57

Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.

Playout Complexity Estimate

Playouts per second	36648.16 (27.29µs/playout)
Reference Size	509839.91 (1.96µs/playout)
Ratio (low is good)	13.91

Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.

State Space Complexity

% new positions/bucket

State Space Complexity	62564205
State Space Complexity (log 10)	7.80
Samples	1029612
Confidence	99.93	0: totally unreliable, 100: perfect

State space complexity (where present) is an estimate of the number of distinct game tree reachable through actual play. Over a series of random games, Ai Ai checks each position to see if it is new, or a repeat of a previous position and keeps a total for each game. As the number of games increase, the quantity of new positions seen per game decreases. These games are then partitioned into a number of buckets, and if certain conditions are met, Ai Ai treats the number in each bucket as the start of a strictly decreasing geometric sequence and sums it to estimate the total state space. The accuracy is calculated as 1-[end bucket count]/[starting bucklet count]

Playout/Search Speed

Label	Its/s	SD	Nodes/s	SD	Game length	SD
Random playout	41,243	1,264	2,789,397	85,563	68	7
search.UCT	42,208	1,650			61	3

Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.

Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.

Mirroring Strategies

Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.

Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.

Win % By Player (Bias)

1: Red win %	56.50±3.09	Includes draws = 50%
2: Black win %	43.50±3.04	Includes draws = 50%
Draw %	0.00	Percentage of games where all players draw.
Decisive %	100.00	Percentage of games with a single winner.
Samples	1000	Quantity of logged games played

Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)

Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.

UCT Skill Chains

Match	AI	Strong Wins	Draws	Strong Losses	#Games	Strong Score	p1 Win%	Draw%	p2 Win%	Game Length
0	Random
1	UCT (its=2)	631	0	352	983	0.6114 <= 0.6419 <= 0.6713	55.04	0.00	44.96	67.10
3	UCT (its=4)	631	0	338	969	0.6206 <= 0.6512 <= 0.6805	56.35	0.00	43.65	66.75
6	UCT (its=7)	631	0	351	982	0.6121 <= 0.6426 <= 0.6719	54.38	0.00	45.62	67.16
9	UCT (its=24)	631	0	125	756	0.8065 <= 0.8347 <= 0.8594	51.46	0.00	48.54	65.09
10	UCT (its=67)	631	0	181	812	0.7472 <= 0.7771 <= 0.8044	55.79	0.00	44.21	63.85
11	UCT (its=181)	631	0	192	823	0.7366 <= 0.7667 <= 0.7943	54.31	0.00	45.69	63.01
12	UCT (its=491)	631	0	181	812	0.7472 <= 0.7771 <= 0.8044	54.80	0.00	45.20	62.06
13	UCT (its=1336)	631	0	181	812	0.7472 <= 0.7771 <= 0.8044	56.28	0.00	43.72	61.29
14	UCT (its=3631)	631	0	241	872	0.6930 <= 0.7236 <= 0.7523	54.70	0.00	45.30	61.10
15	UCT (its=3631)	500	0	500	1000	0.4691 <= 0.5000 <= 0.5309	56.00	0.00	44.00	61.13

Search for levels ended: time limit reached.

Level of Play: Strong beats Weak 60% of the time (lower bound with 95% confidence).

Draw%, p1 win% and game length may give some indication of trends as AI strength increases.

1st Player Win Ratios by Playing Strength

This chart shows the win(green)/draw(black)/loss(red) percentages, as UCT play strength increases. Note that for most games, the top playing strength show here will be distinctly below human standard.

Complexity

Game length	60.63
Branching factor	7.39
Complexity	10^50.56	Based on game length and branching factor
Computational Complexity	10^7.24	Sample quality (100 best): 0.94
Samples	1000	Quantity of logged games played

Computational complexity (where present) is an estimate of the game tree reachable through actual play. For each game in turn, Ai Ai marks the positions reached in a hashtable, then counts the number of new moves added to the table. Once all moves are applied, it treats this sequence as a geometric progression and calculates the sum as n-> infinity.

Move Classification

Board Size	61	Quantity of distinct board cells
Distinct actions	311	Quantity of distinct moves (e.g. "e4") regardless of position in game tree
Killer moves	1	A 'killer' move is selected by the AI more than 50% of the time Killers: h5-i5
Good moves	178	A good move is selected by the AI more than the average
Bad moves	133	A bad move is selected by the AI less than the average
Terrible moves	3	A terrible move is never selected by the AI Terrible moves: b5-a5,h2-i1,e8-e9
Response distance%	42.25%	Distance from move to response / maximum board distance; a low value suggests a game is tactical rather than strategic.
Samples	1000	Quantity of logged games played

Board Coverage

A mean of 96.26% of board locations were used per game.

Colour and size show the frequency of visits.

Game Length

Game length frequencies.

Mean	60.63
Mode	[59]
Median	60.0

Change in Material Per Turn

Mean change in material/round	0.00	Complete round of play (all players)

This chart is based on a single representative* playout, and gives a feel for the change in material over the course of a game. (* Representative in the sense that it is close to the mean length.)

Actions/turn

Table: branching factor per turn, based on a single representative* game. (* Representative in the sense that it is close to the mean game length.)

Action Types per Turn

This chart is based on a single representative* game, and gives a feel for the types of moves available throughout that game. (* Representative in the sense that it is close to the mean game length.)

Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.

Trajectory

This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).

The lead changed on 6% of the game turns. Ai Ai found 7 critical turns (turns with only one good option).

Position Heatmap

This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).

Good/Effective moves

Measure	All players	Player 1	Player 2
Mean % of effective moves	50.72	36.86	65.04
Mean no. of effective moves	3.59	2.77	4.43
Effective game space	10^29.04	10^11.16	10^17.88
Mean % of good moves	25.16	43.49	6.22
Mean no. of good moves	1.74	3.03	0.40
Good move game space	10^13.36	10^12.10	10^1.26

These figures were calculated over a single game.

An effective move is one with score 0.1 of the best move (including the best move). -1 (loss) <= score <= 1 (win)

A good move has a score > 0. Note that when there are no good moves, an multiplier of 1 is used for the game space calculation.

Quality Measures

Measure	Value	Description
Hot turns	78.69%	A hot turn is one where making a move is better than doing nothing.
Momentum	18.03%	% of turns where a player improved their score.
Correction	40.98%	% of turns where the score headed back towards equality.
Depth	6.34%	Difference in evaluation between a short and long search.
Drama	0.11%	How much the winner was behind before their final victory.
Foulup Factor	22.95%	Moves that looked better than the best move after a short search.
Surprising turns	6.56%	Turns that looked bad after a short search, but good after a long one.
Last lead change	60.66%	Distance through game when the lead changed for the last time.
Decisiveness	22.95%	Distance from the result being known to the end of the game.

These figures were calculated over a single representative* game, and based on the measures of quality described in "Automatic Generation and Evaluation of Recombination Games" (Cameron Browne, 2007). (* Representative, in the sense that it is close to the mean game length.)

Openings

Moves	Animation
e1-f1,i1-i2,f1-g1,e9-e8,g1-h1,i2-h2,h1-g2
e1-f1,e9-e8,f1-g1,i1-i2,g1-h1,i2-h2,h1-g2
e1-d2,i1-i2,i5-i4,e9-d9,i4-i3,d9-c9,a9-b8
e1-d2,e9-d9,i5-i4,i1-i2,i4-i3,d9-c9,a9-b8
e1-e2,i1-h1,e2-f1,a5-a6,f1-g1,h1-g2,g1-f2
e1-e2,a5-a6,e2-f1,i1-h1,f1-g1,h1-g2,g1-f2
i5-i4,i1-i2,e1-d2,e9-d9,i4-i3,d9-c9,a9-b8
i5-i4,e9-d9,e1-d2,i1-i2,i4-i3,d9-c9,a9-b8
e1-e2,i1-h2,i5-i4,e9-e8,a9-a8,h2-h3
e1-e2,e9-e8,i5-i4,i1-h2,a9-a8,h2-h3
i5-i4,i1-h2,e1-e2,e9-e8,a9-a8,h2-h3
i5-i4,e9-e8,e1-e2,i1-h2,a9-a8,h2-h3

Opening Heatmap

Colour shows the success ratio of this play over the first 10moves; black < red < yellow < white.

Size shows the frequency this move is played.

Unique Positions Reachable at Depth

0	1	2	3	4	5	6	7	8	9
1	9	90	630	4224	24942	143580	762696	3962137	19478540

Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.

Shortest Game(s)

No solutions found to depth 9.

Puzzles

Puzzle	Solution
Red to win in 13 moves
Red to win in 11 moves
Black to win in 11 moves
Black to win in 9 moves
Red to win in 11 moves
Black to win in 5 moves
Red to win in 5 moves
Red to win in 9 moves
Black to win in 7 moves
Red to win in 5 moves
Black to win in 3 moves
Red to win in 3 moves

Selection criteria: first move must be unique, and not forced to avoid losing. Beyond that, Puzzles will be rated by the product of [total move]/[best moves] at each step, and the best puzzles selected.