Full Report for Keil by Luis Bolaños Mures

Rules

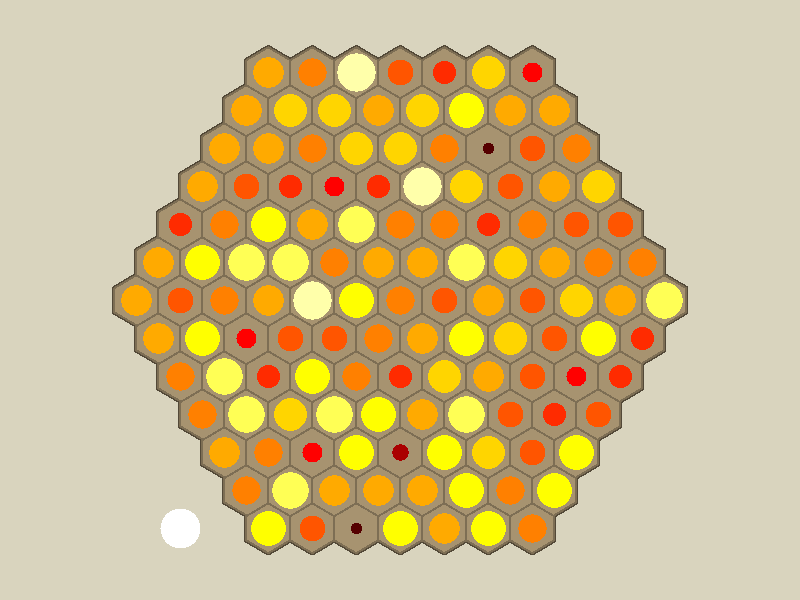
Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!

Definitions

Two adjacent same-colour stones, or a stone and an adjacent empty point, are linked if there is another point adjacent to both that is not occupied by the other colour. Two adjacent empty points, on the other hand, are always linked.

A group is a stone together with all other stones one could reach from it through a series of steps between linked stones. Since only same-colour stones are linked, all stones in a group are the same colour.

A liberty of a group is an empty point linked to at least one stone in that group.

Similarly, a territory is an empty point together with all other empty points one could reach from it through a series of steps between linked empty points. You own a territory if all stones linked to points in that territory are of your colour.

Play

Black plays first, then turns alternate. On your turn, you must pass or place a stone of your colour on an empty point. After a placement, remove all enemy stones in groups without liberties. After all removals, the stone you placed must be part of a group with at least one liberty, and the current board position must be different from the board positions at the end of all your previous turns. Otherwise, your placement is illegal.

The game ends when both players pass in succession. The player with the higher score in the final position wins. A player's score is the number of stones of their colour on the board, plus the number of points in their territories, plus a komi in the case of White. The button may be used to break ties.

Komi and button

The komi is the number of points which is added to White's score at the end of the game as a compensation for playing second. Before the game starts, the first player chooses the value of komi, and then the second player chooses sides. Alternatively, both players may just agree on a value. To avoid ties, it is suggested to either set komi to half a point higher than a whole number (like 6.5) or to use a whole value along with the button.

The button is a special token which is placed next to the board at the start of the game. On your turn, if neither player has taken the button yet, you may not pass, but you may take the button instead of making a board play. At the end of the game, a half point is added to the score of the player who has taken the button. When checking for repetitions, two identical board positions are still considered different if the button had already been taken in one of them but not in the other.

Miscellaneous

General comments:

Play: Combinatorial

Family: Combinatorial 2019,Go

Mechanism(s): Capture,Scoring

Components: Board

Level: Standard

BGG Stats

BGG Ratings and Comments

Kolomogorov Complexity Analysis

Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.

Playout Complexity Estimate

Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.

Playout/Search Speed

Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.

Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.

Mirroring Strategies

Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.

Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.

Win % By Player (Bias)

Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)

Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.

Levels of Play

Level of Play: Strong beats Weak 60% of the time (lower bound with 90% confidence).

Draw%, p1 win% and game length may give some indication of trends as AI strength increases; but be aware that the AI can introduce bias due to horizon effects, poor heuristics, etc.

Complexity

Computational complexity (where present) is an estimate of the game tree reachable through actual play. For each game in turn, Ai Ai marks the positions reached in a hashtable, then counts the number of new moves added to the table. Once all moves are applied, it treats this sequence as a geometric progression and calculates the sum as n-> infinity.

Move Classification

Board Coverage

A mean of 30.85% of board locations were used per game.

Colour and size show the frequency of visits.

Game Length

Game length frequencies.

Change in Material Per Turn

This chart is based on a single representative* playout, and gives a feel for the change in material over the course of a game. (* Representative in the sense that it is close to the mean length.)

Actions/turn

Table: branching factor per turn, based on a single representative* game. (* Representative in the sense that it is close to the mean game length.)

Action Types per Turn

This chart is based on a single representative* game, and gives a feel for the types of moves available throughout that game. (* Representative in the sense that it is close to the mean game length.)

Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.

Opening Heatmap

Colour shows the success ratio of this play over the first 10moves; black < red < yellow < white.

Size shows the frequency this move is played.

Unique Positions Reachable at Depth

Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.

Shortest Game(s)

No solutions found to depth 3.