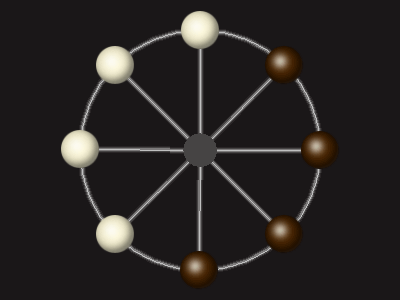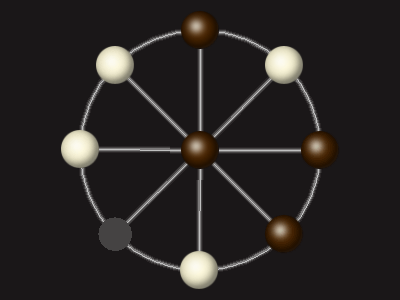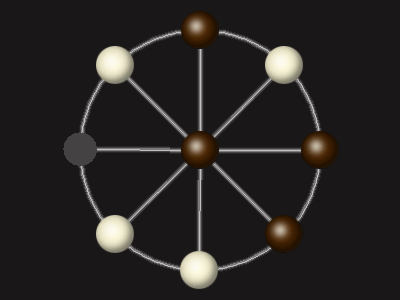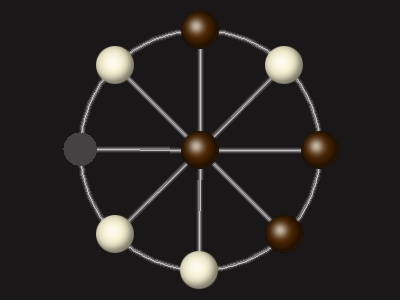
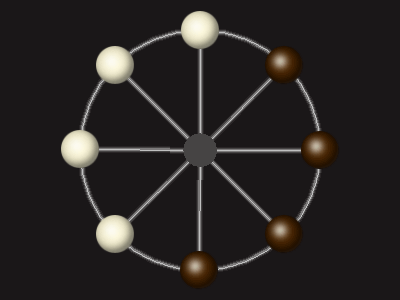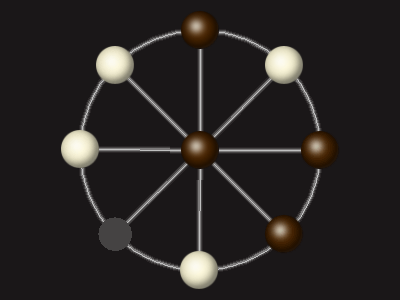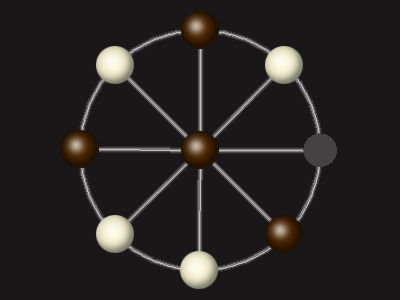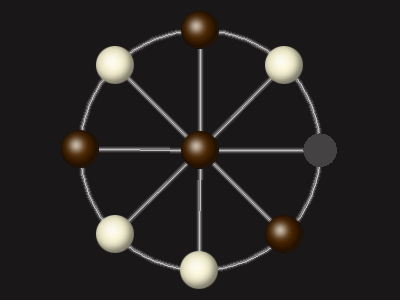
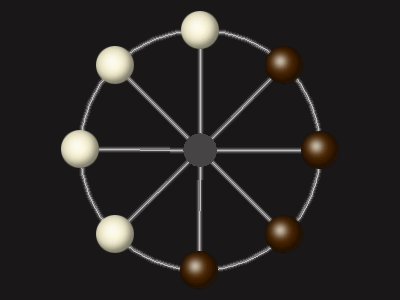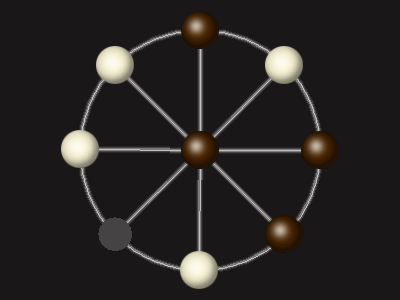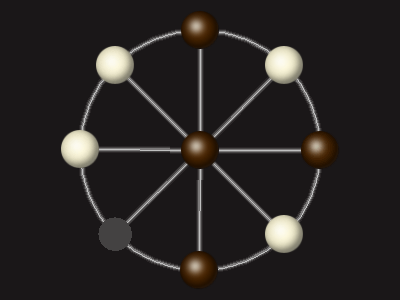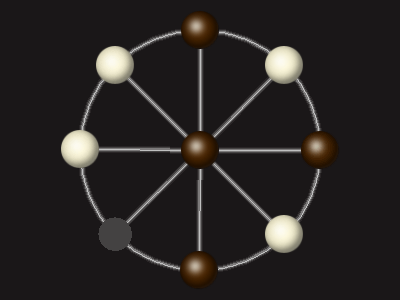
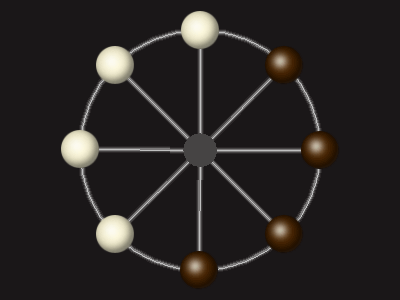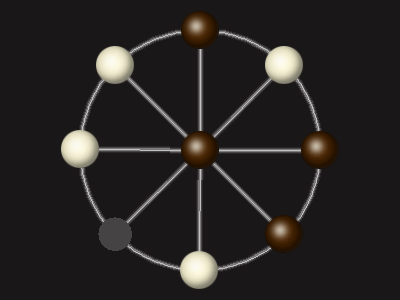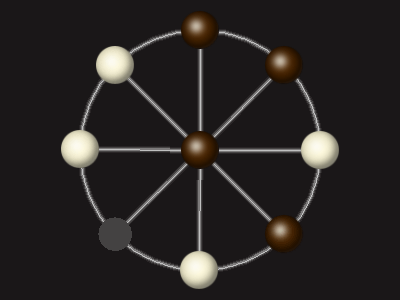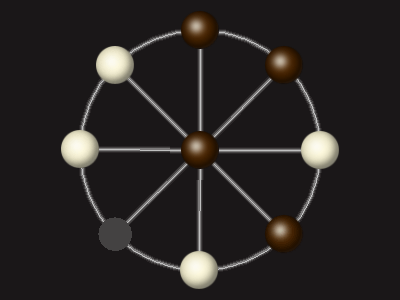
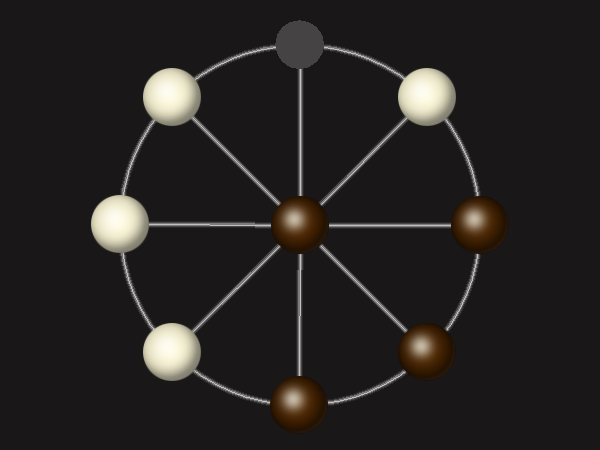
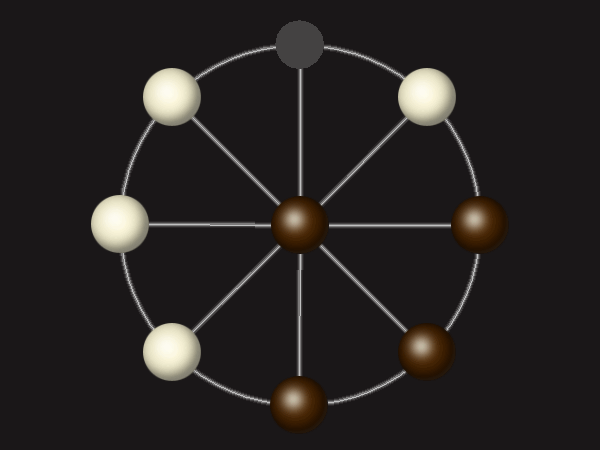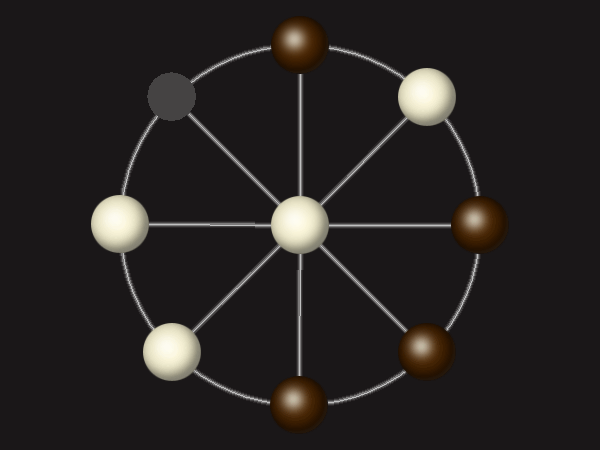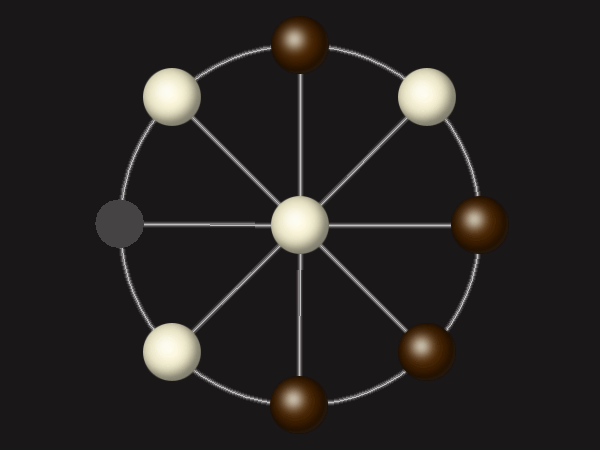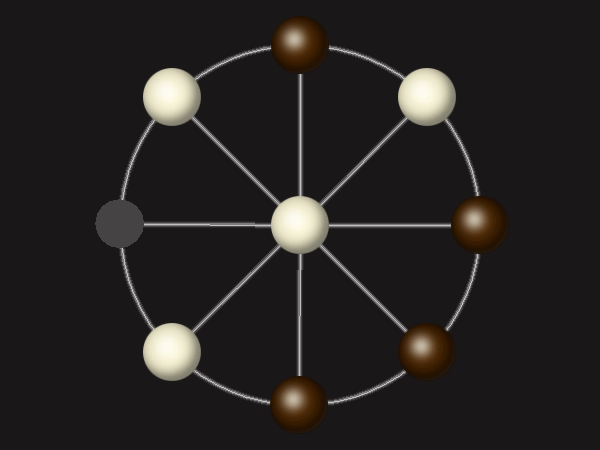
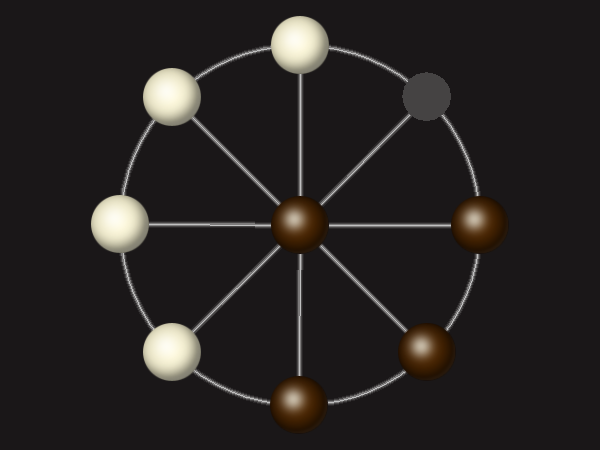
Rules
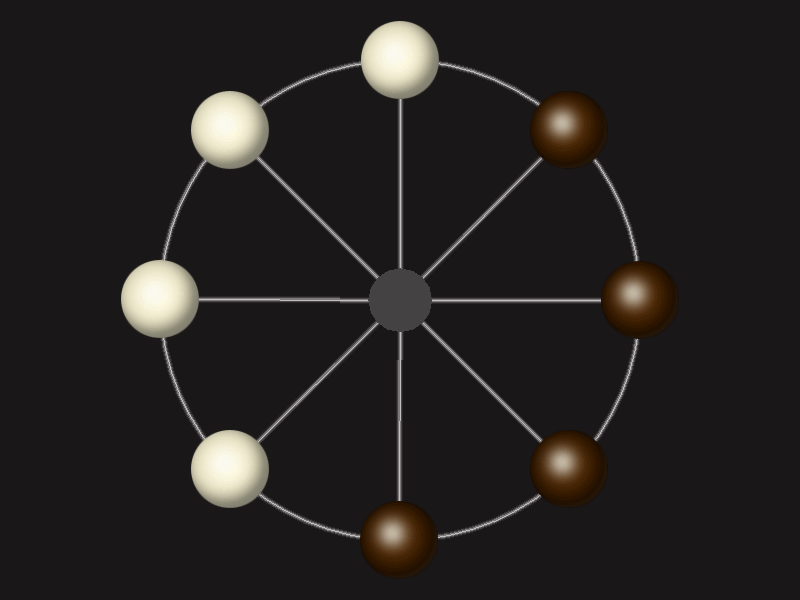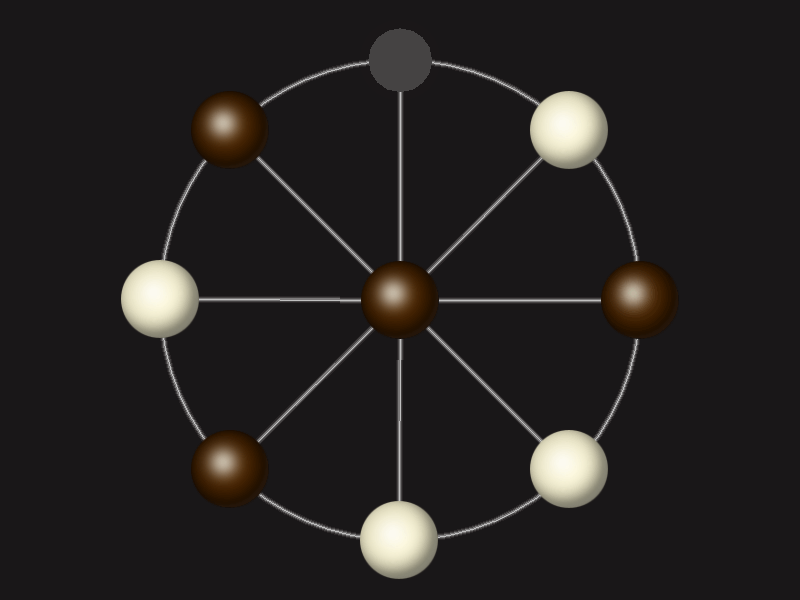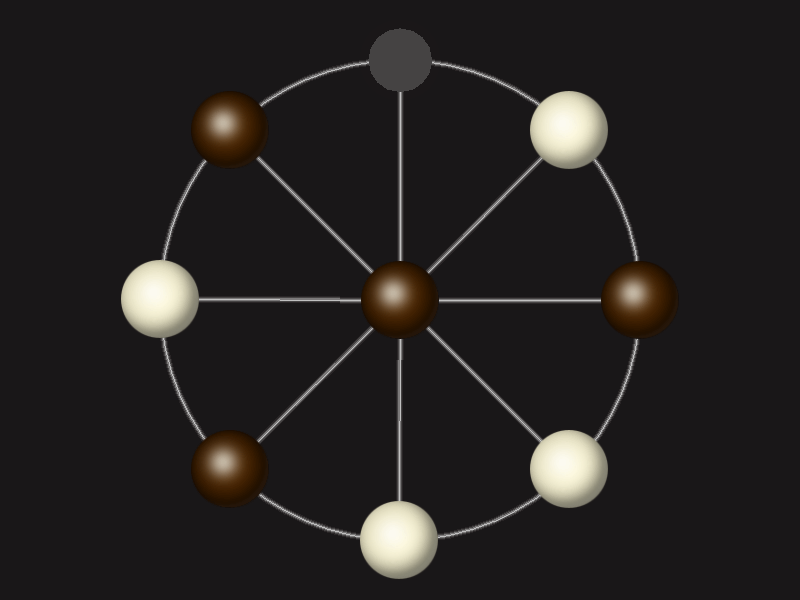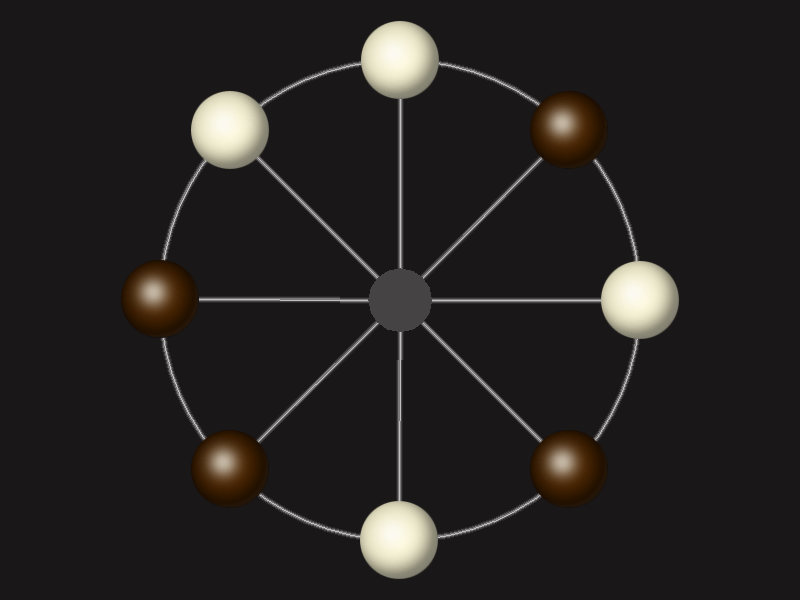
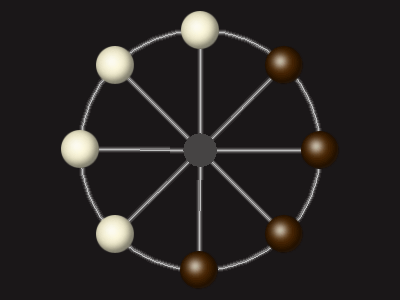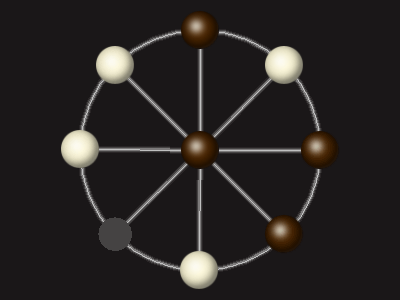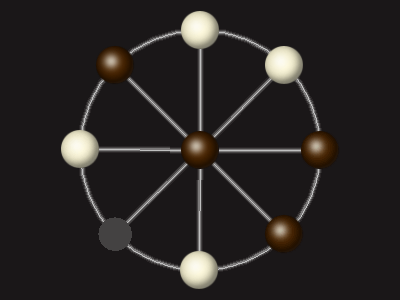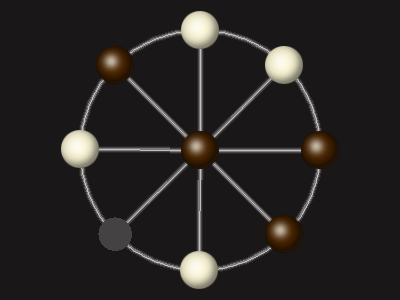
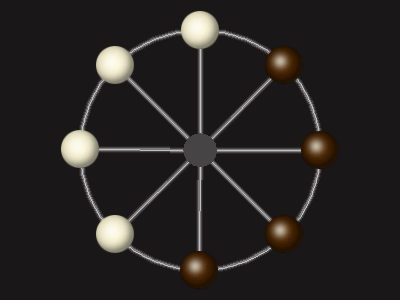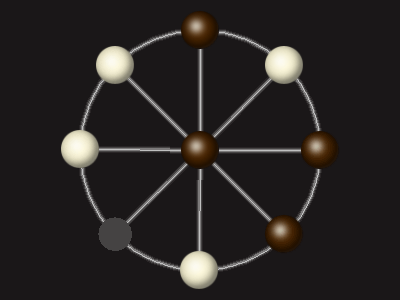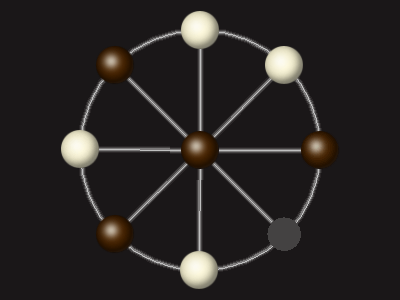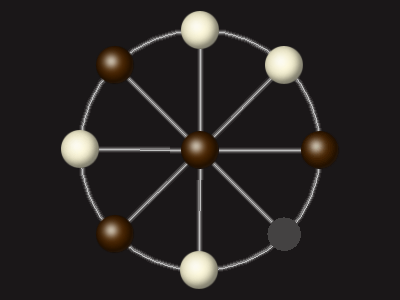
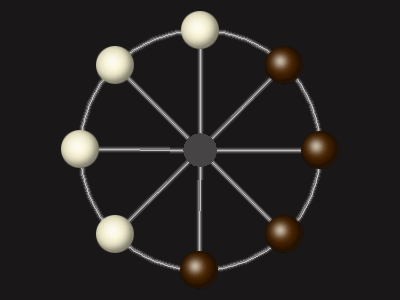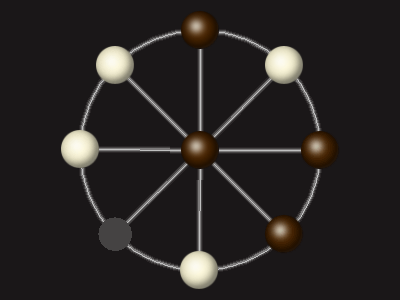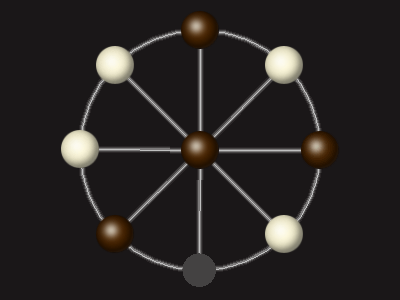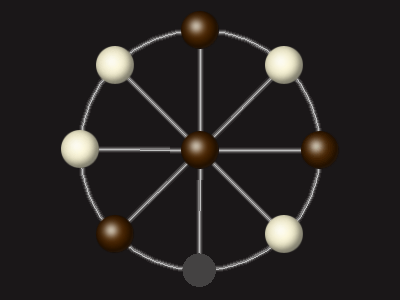
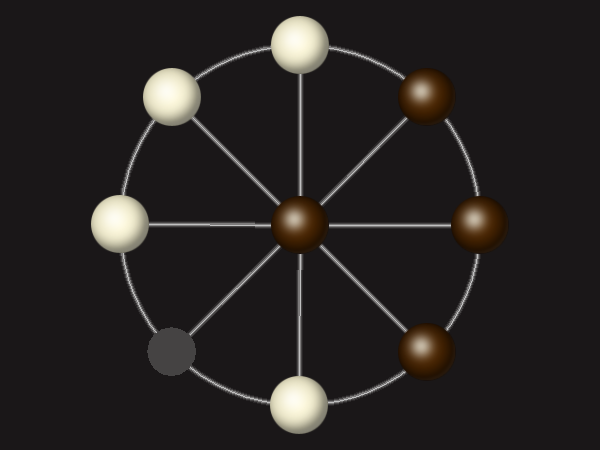
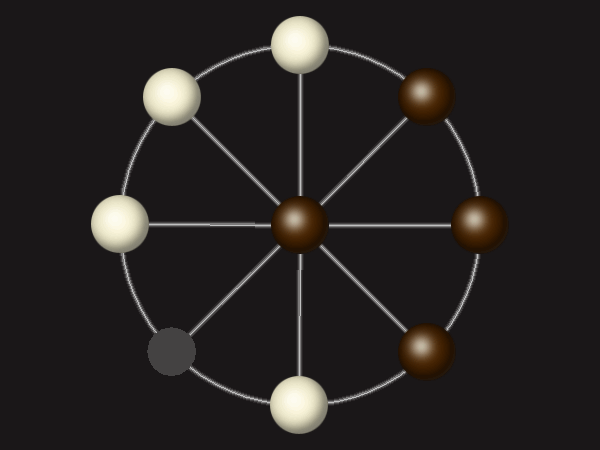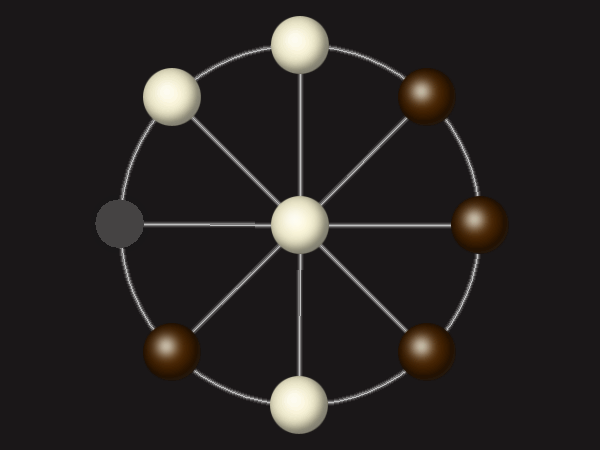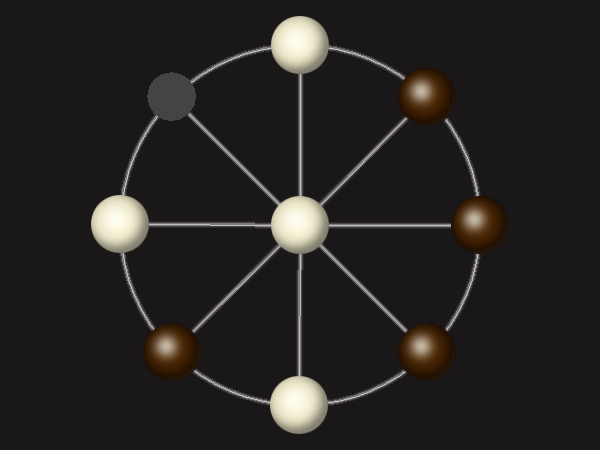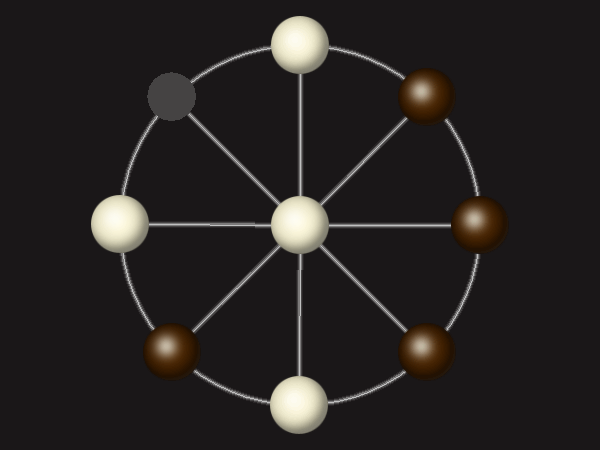
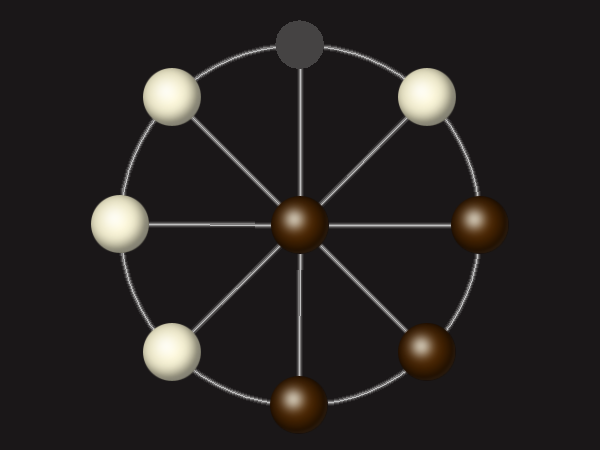
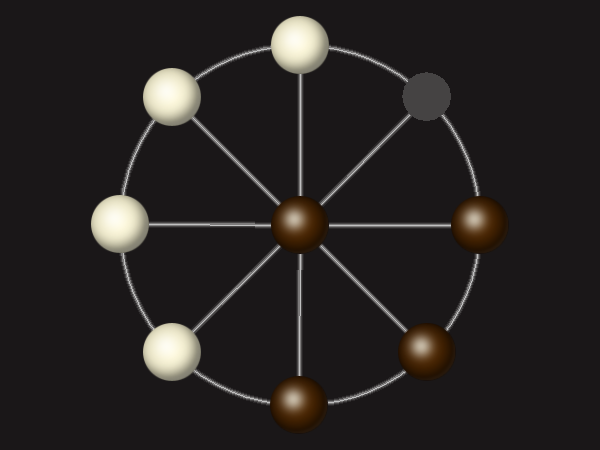
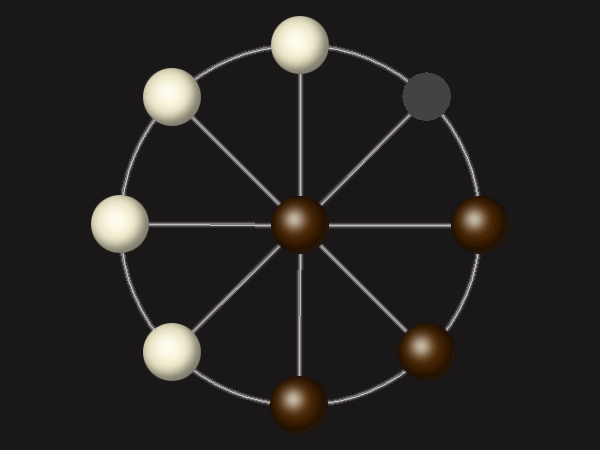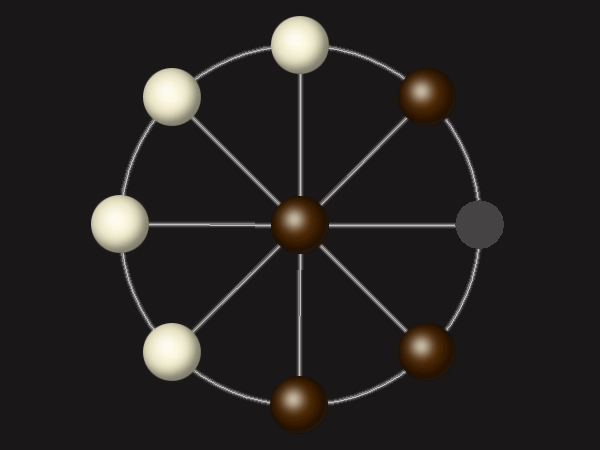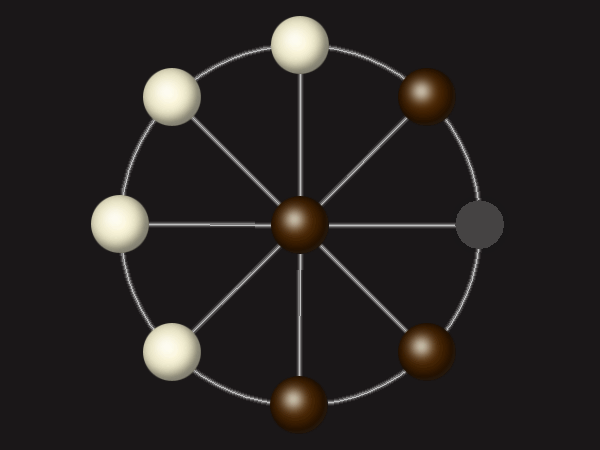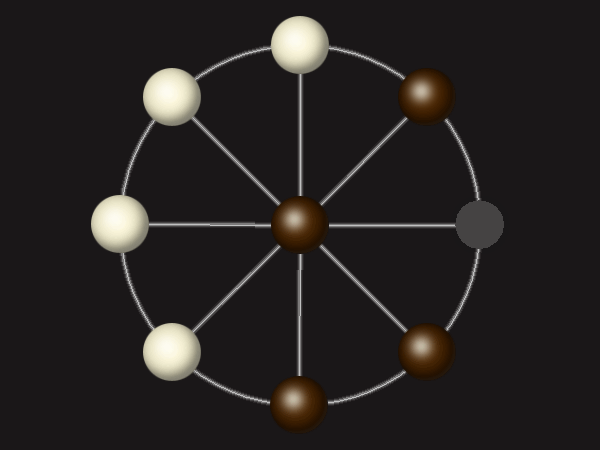
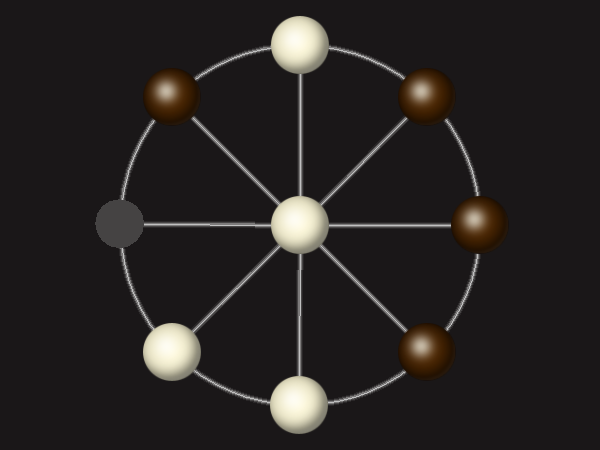
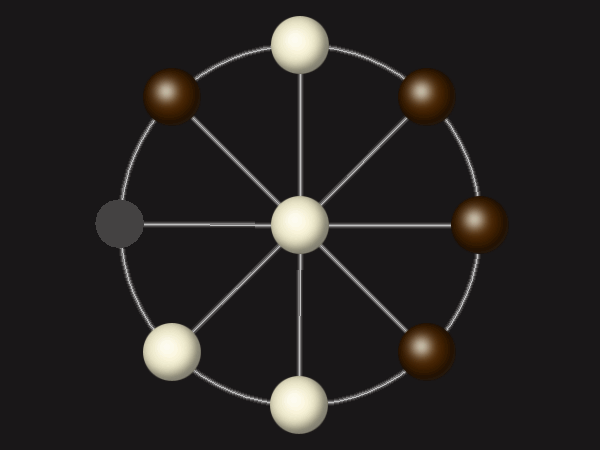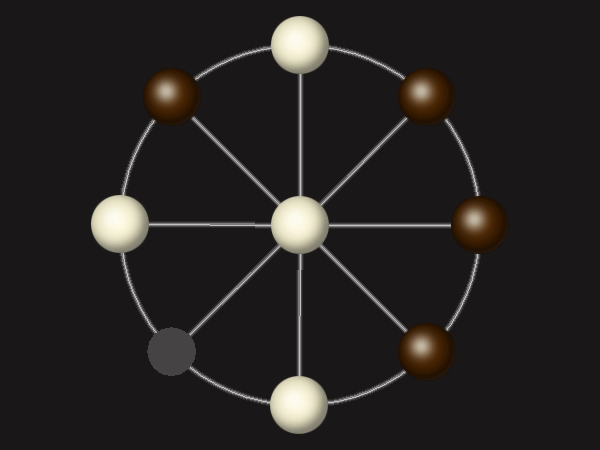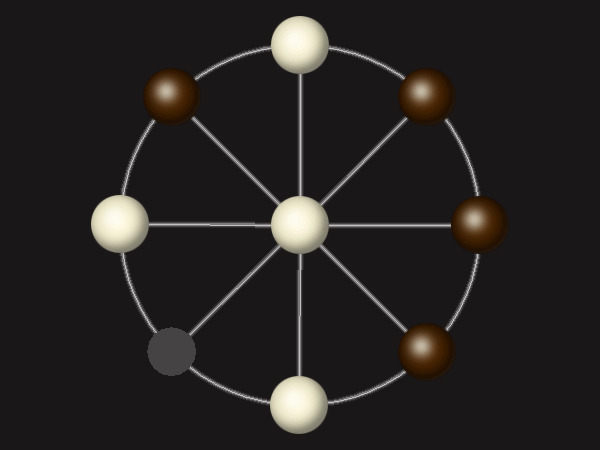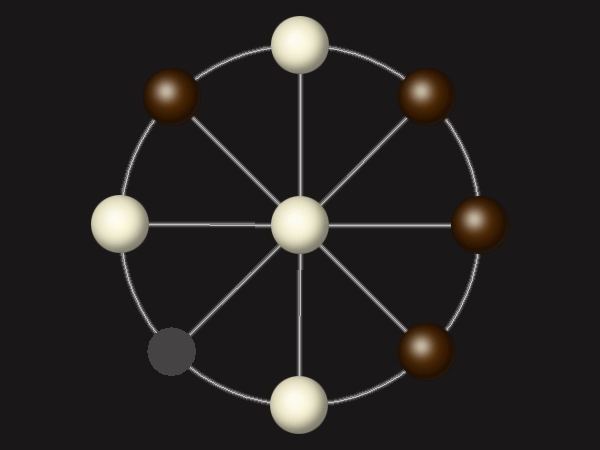
Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!
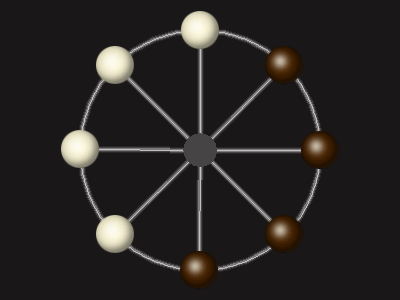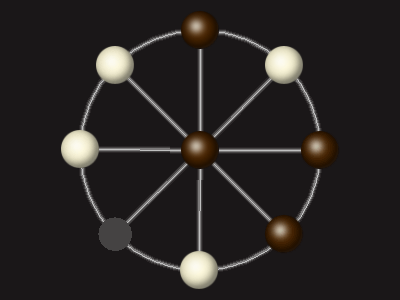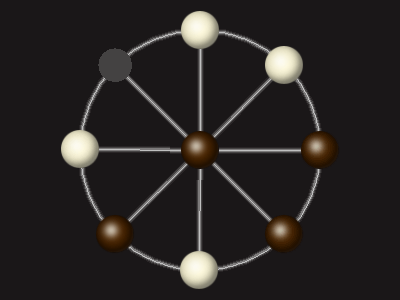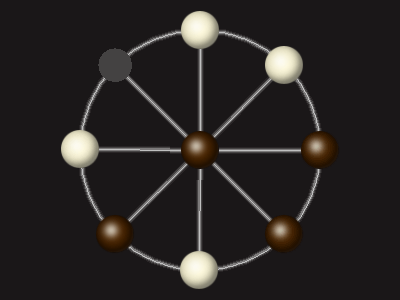
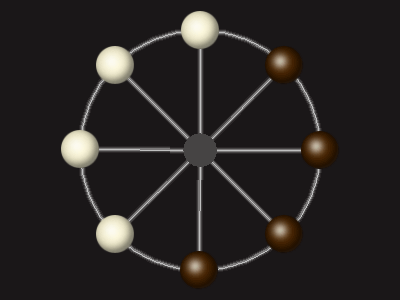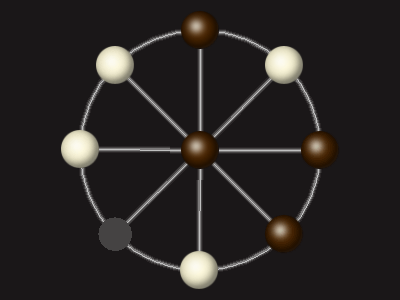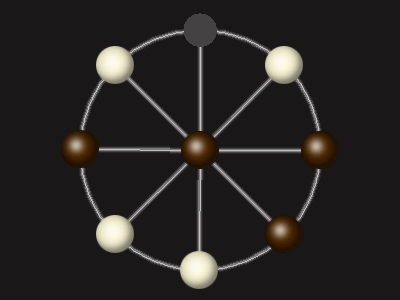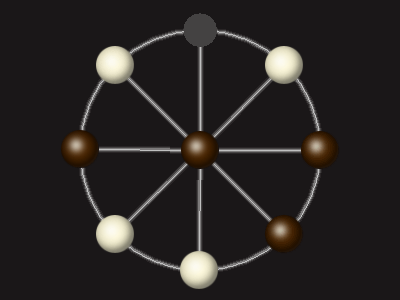
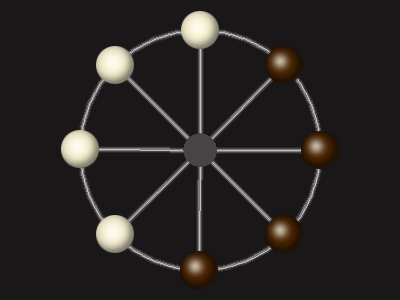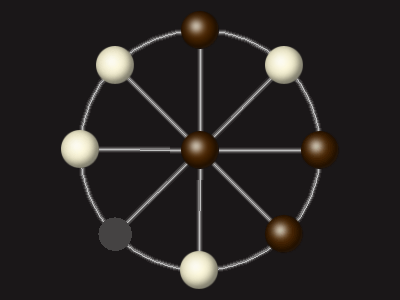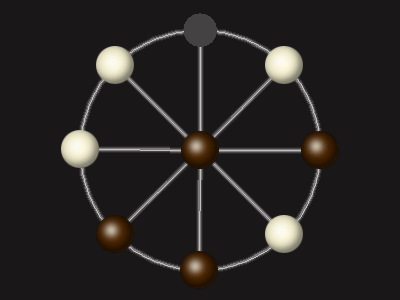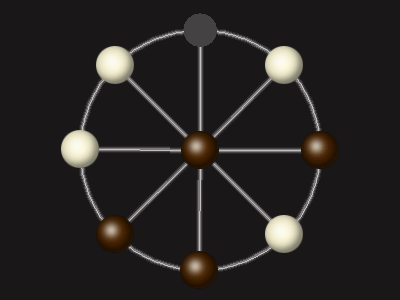
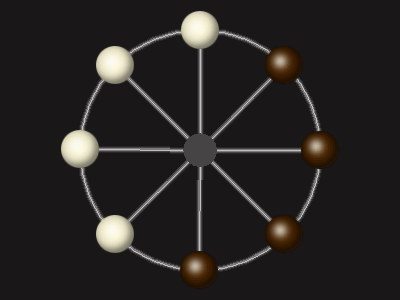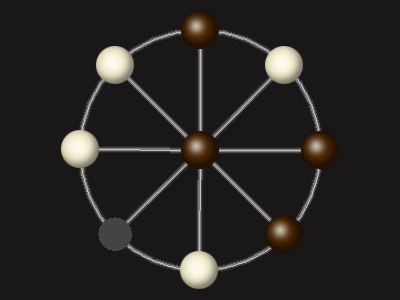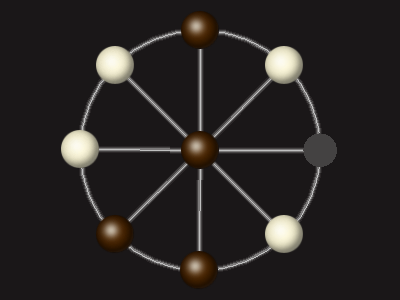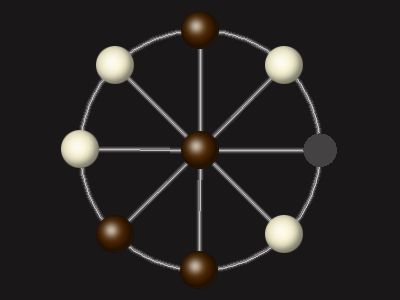
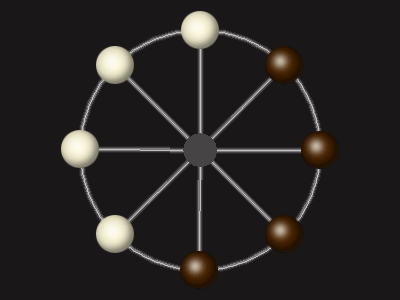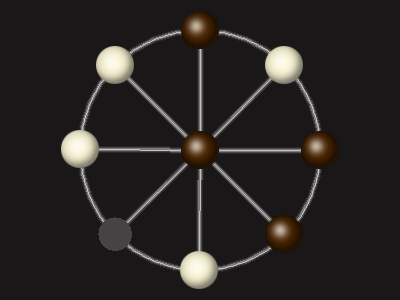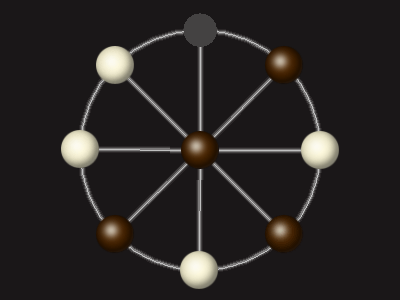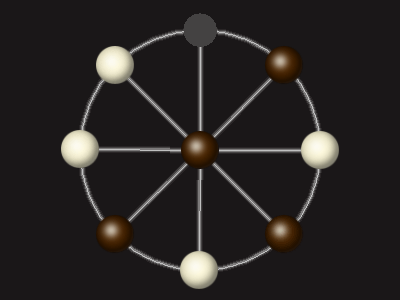
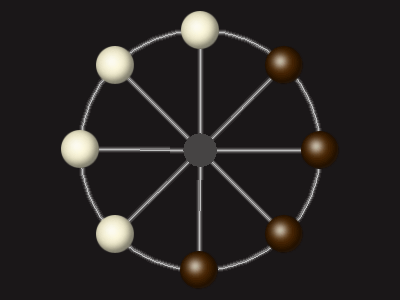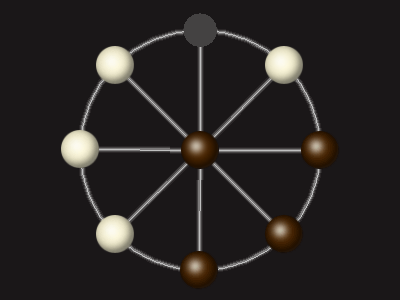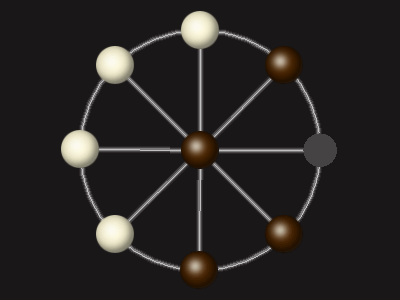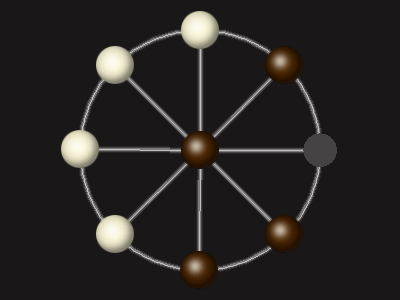
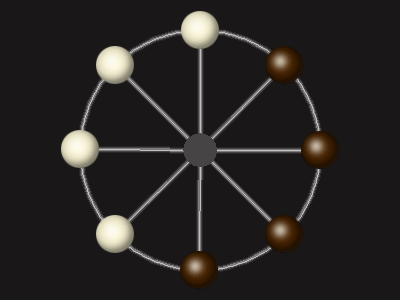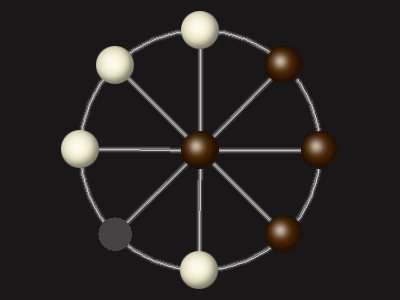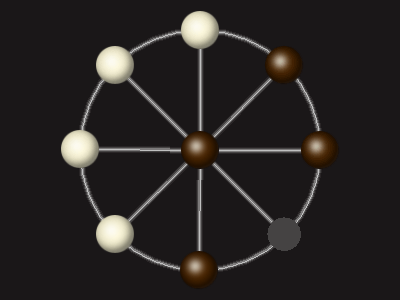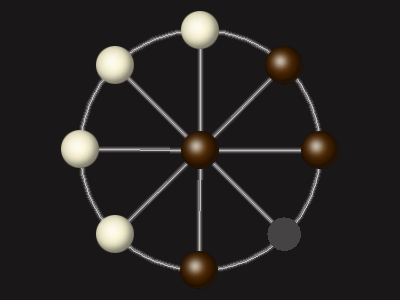
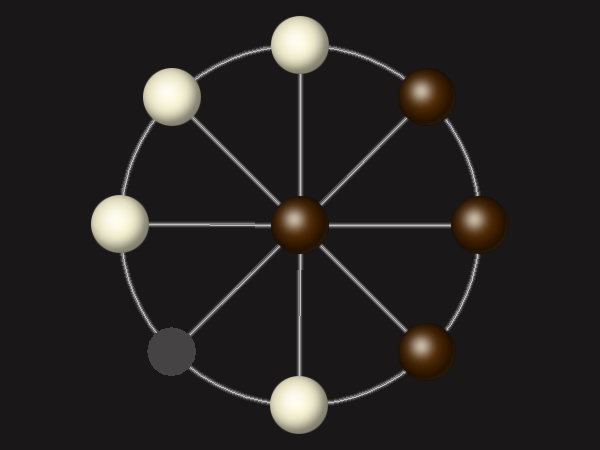
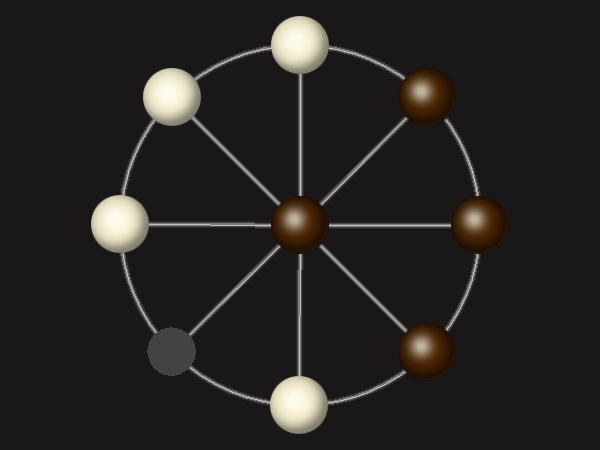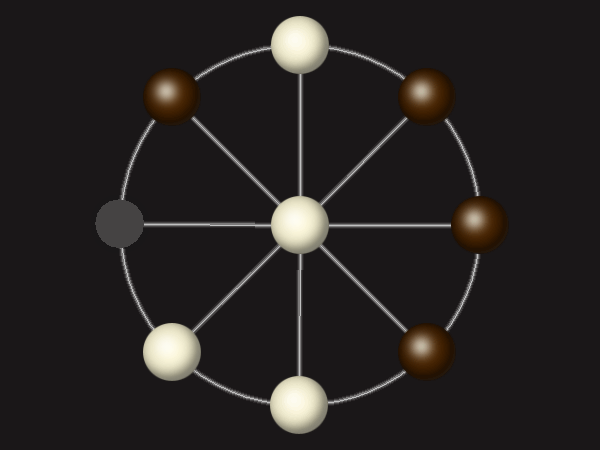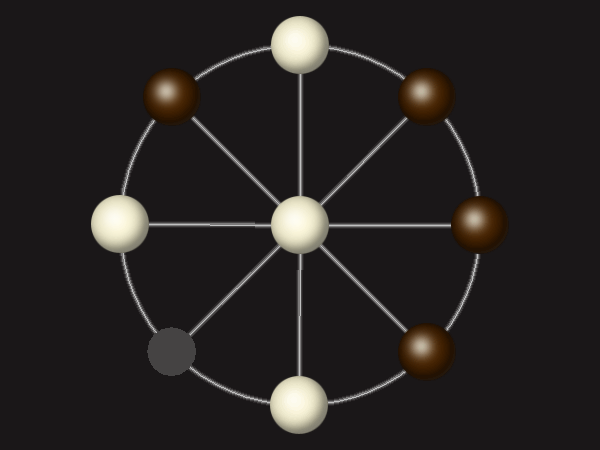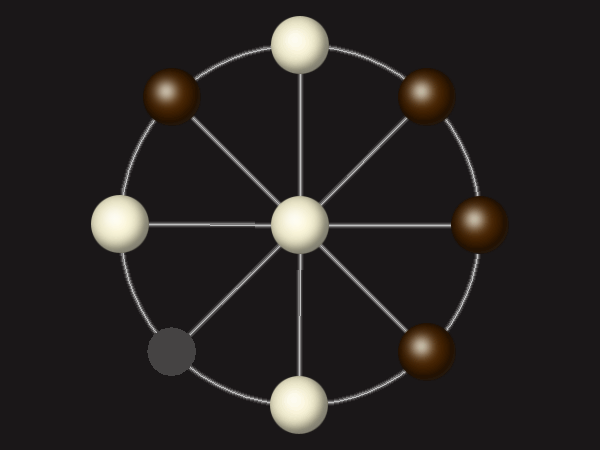
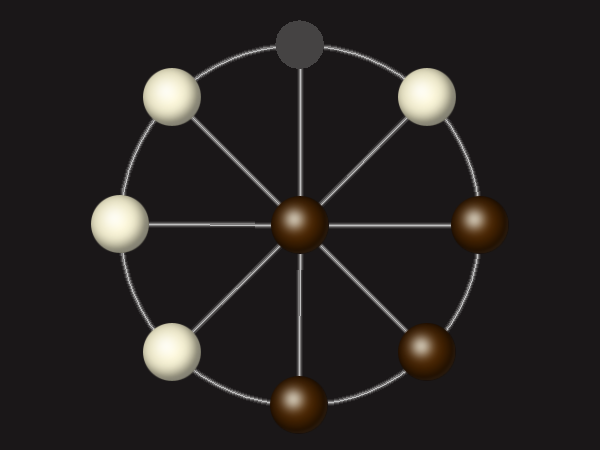
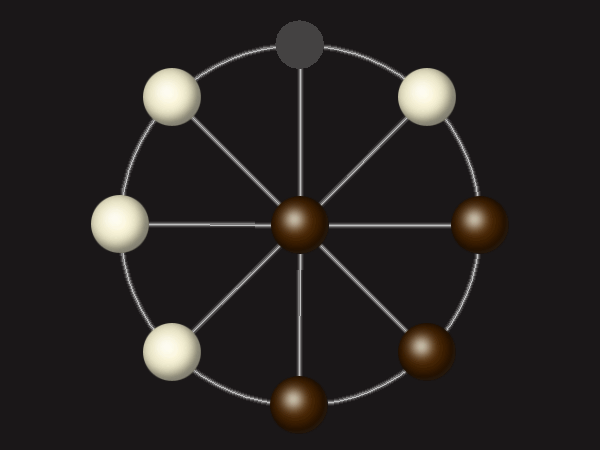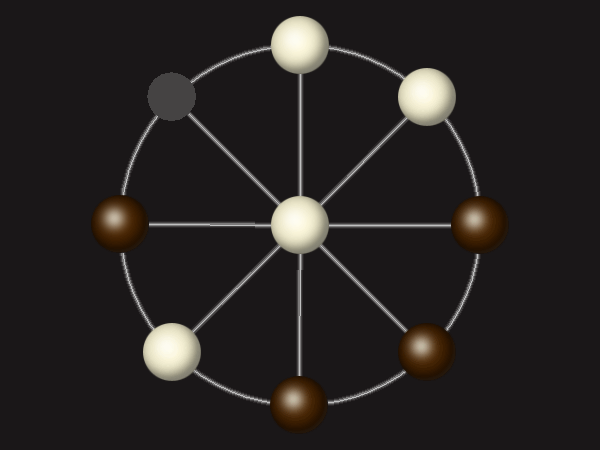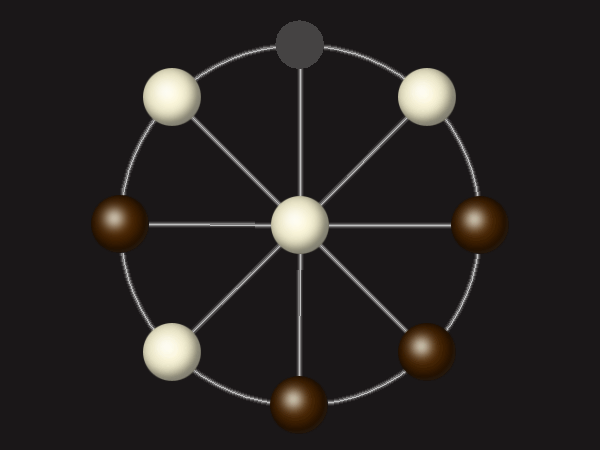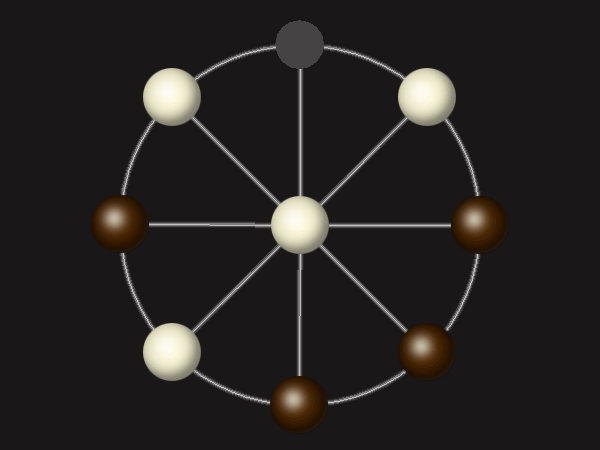
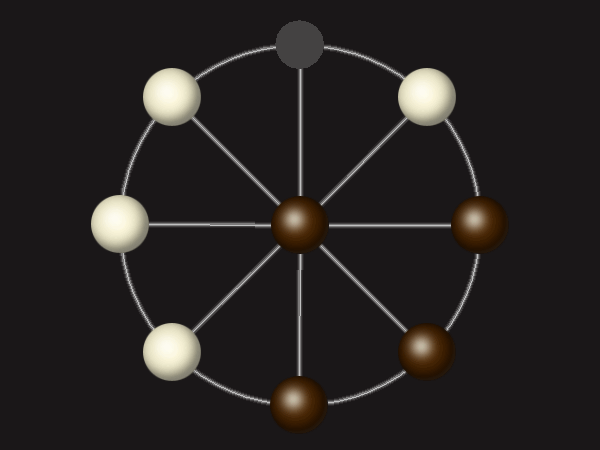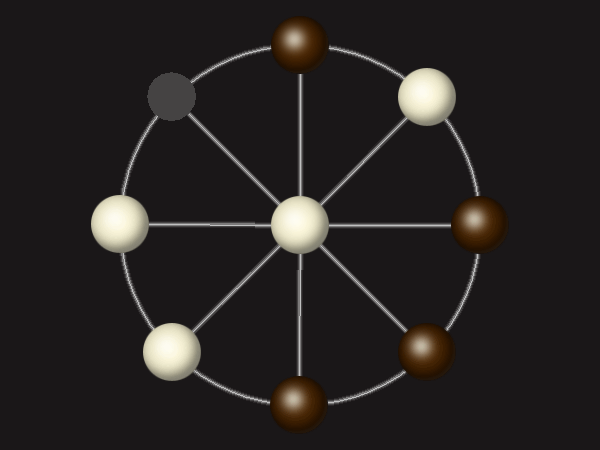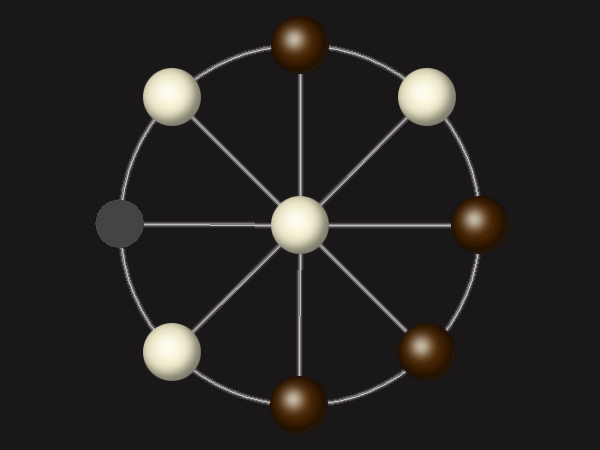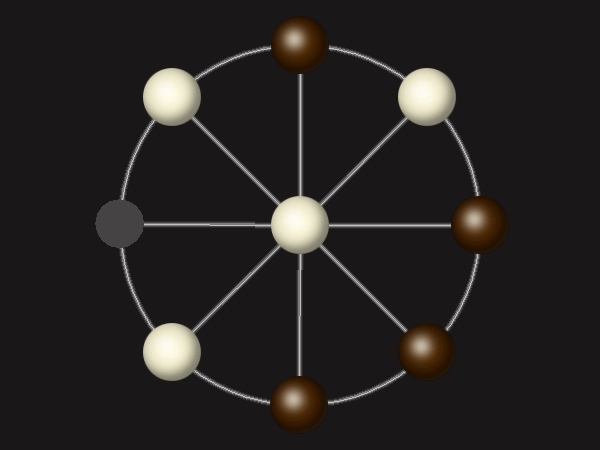
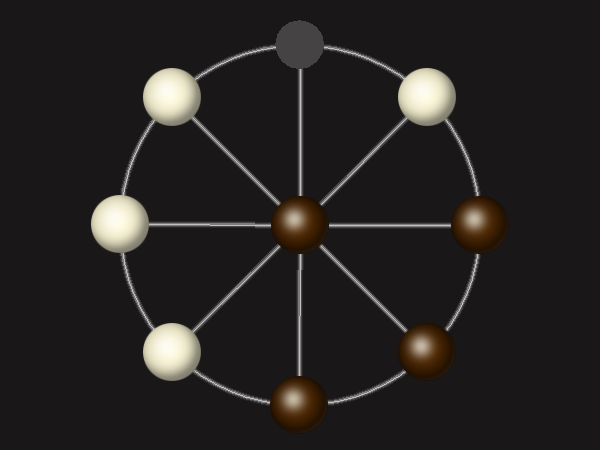
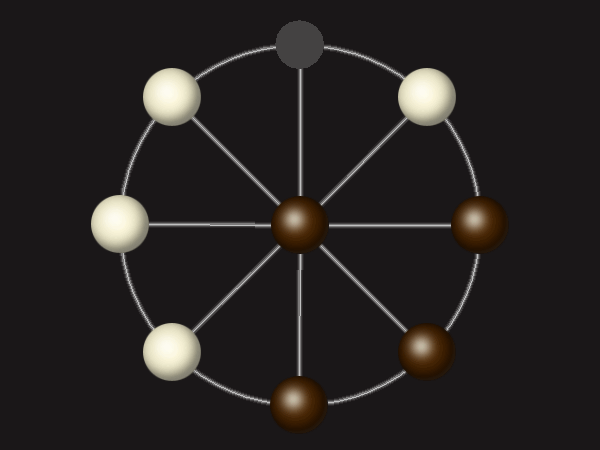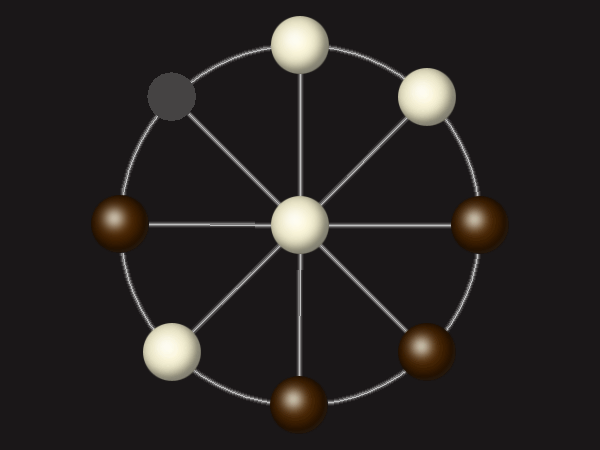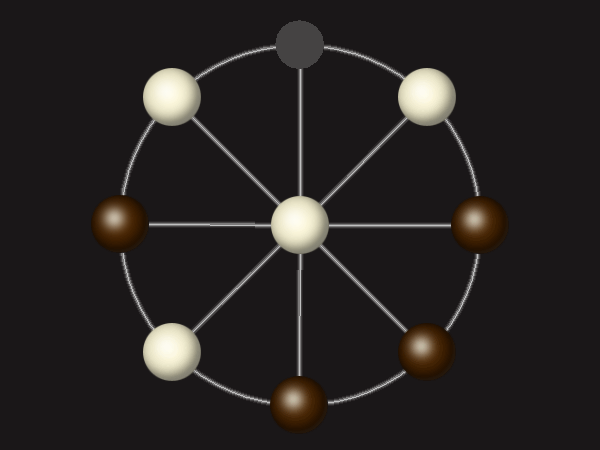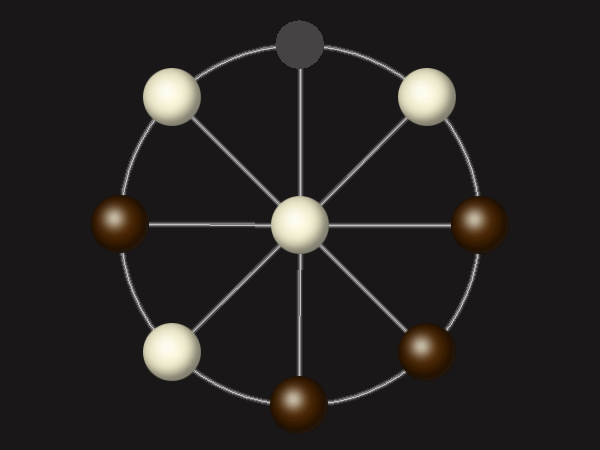
Goal
Stalemate the opponent to win.
Rules
Each turn, move a piece along a line to the empty space. A piece can only move to the centre if it is adjacent to an enemy piece.