Change in Material Per Turn
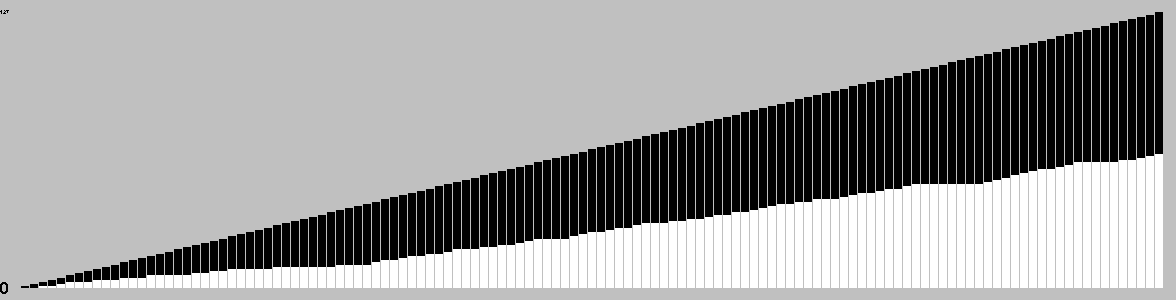
This chart is based on a single playout, and gives a feel for the change in material over the course of a game.
Place a piece of either colour; when the board is full, player 1 wins if there are an odd number of groups, player 2 otherwise.
Definition: A Group is a set of connected, like-colored stones on the board, containing at least N stones (where N is the length of one side of the board).
Players take turns. On your turn you must place either one black stone or one white stone onto any empty space.
The game ends when the board is full. Player 1 wins if there is an odd number of groups on the board (counting both black and white groups); Player 2 wins otherwise.
General comments:
Play: Combinatorial
Mechanism(s): Strict Placement
Components: Board
| BGG Entry | Odd |
|---|---|
| BGG Rating | 6.66667 |
| #Voters | 12 |
| SD | 1.43372 |
| BGG Weight | 2 |
| #Voters | 1 |
| Year | 2007 |
| User | Rating | Comment |
|---|---|---|
| pecan | 5 | |
| rseater | 4 | It's a fresh variation of normal abstracts, but I found the early game too undirected. I'd rather start in a half-completed random state, then try to predict which side could win. I'm a fan of the designer, but this one doesn't do it for me. |
| mrraow | 7 | Simple, interesting game with interesting decisions to be made even early on. It also has the dubious merit of being the only one of Nick's games that was easy to implement in Ai AI! |
| milomilo122 | N/A | I'm the designer. Over the years I've come to see this as one of my best abstract games, but it's also my most misunderstood game. The rules are as simple as they come, but they don't give much indication of how to think about the game, or how it feels to play once you know what you're doing. This is especially true for the opening. New players often have no idea how to approach it, and will conclude it's irredeemably opaque. It isn't. With experience, Odd is clear and strategic from the beginning, clear enough that experienced plays often choose to play larger boards or reduce the minimum group size a little to make it *more* opaque. The disconnect between first impression and seasoned play keeps people from seeing what it's really about before they dismiss it. Accordingly, it doesn't get as much attention as some of my other designs. Too bad, because I cherish it. Some features I like, from a design aesthetic point of view: 1. Because you can play pieces of either color, the game has a big branch factor despite a small board and the simplest possible turn structure. Relatedly, there's a big difference between how simple the game looks on the surface and how gnarly it is strategically. It's a deep connection game masquerading as something else. 2. I like that there are no restrictions on where you can place your pieces. You never have moments where you're like: "oh yeah, right, I forgot I can't do that". This has become an increasingly important principle in my design aesthetic over the years. There's a smooth ease to games with this quality that's important to me. 3. The game is quite balanced (or rather can be balanced for the right choice of minimum group size in relation to board size; I don't know if I've gotten it right), it always terminates, and draws are naturally impossible. |
| simpledeep | 9 | |
| njking | 6 | |
| schwarzspecht | 8 | |
| ervandarnell | 6 | A subsequent play did not confirm my initial impression. Both odd and even seem about equally possible. One game ended with a 3-legged star of black and 3 white regions in between (victory for even). The other game ended with white strip, black strip, white strip, victory for odd, but there were several orphaned 4-groups that could have changed the outcome. I also came to appreciate, beyond the tactical aspect, a nim-like (or ko-battle like) aspect to threatening various connections inducing other such threats elsewhere. This adds another dimension to the overall strategy. earlier: On the prescribed size board, it seems to degenerate to 3 groups, and the only question is if the even player can sabotage this with a connection, or maybe, just maybe sneak in a fourth, but in either case there isn't much room for play. Should try on a larger board. |
| 4characters | 6 | |
| CDRodeffer | N/A | Not yet played. |
| bluebee2 | N/A | PnP |
| Ikarus | N/A | # P&P |
| grasa_total | 9 | I'm not convinced the first 10-20 moves matter. But I'm not convinced they don't, either. I recommend physically placing some pieces of each color on both sides of the table so people don't fall into a groove of thinking one color is 'theirs'. |
| Kether1983 | 6 | Nagyon kis szuper játék matekórákra. Egyszerű szabályok, kellő mélység. De azért alapvetően nem élvezeti játék, matekórán kívül nem játszanám. :) |
| russ | 7 | There are some surprising interesting tactics to discover. We enjoyed various aha-effects during play. Like Nick's comment notes, the gameplay experience is not obvious from the rules. We both found the game more fun and interesting than we expected just based on the rules. FWIW our first 3 games ended with 3 groups, 4 groups, and 5 groups. (That progression cannot continue indefinitely...) :) |
| oppenheimer | N/A | PnP (from files on BGG); unplayed. |
| nestorgames | 7 |
| AI | Strong Wins | Draws | Strong Losses | #Games | Strong Win% | p1 Win% | Game Length |
|---|---|---|---|---|---|---|---|
| Random | |||||||
| Grand Unified UCT(U1-T,rSel=s, secs=0.01) | 36 | 0 | 0 | 36 | 100.00 | 47.22 | 127.00 |
| Grand Unified UCT(U1-T,rSel=s, secs=0.03) | 36 | 0 | 8 | 44 | 81.82 | 68.18 | 127.00 |
| Grand Unified UCT(U1-T,rSel=s, secs=0.07) | 36 | 0 | 13 | 49 | 73.47 | 48.98 | 127.00 |
| Grand Unified UCT(U1-T,rSel=s, secs=0.20) | 36 | 0 | 4 | 40 | 90.00 | 47.50 | 127.00 |
Level of Play: Strong beats Weak 60% of the time (lower bound with 90% confidence).
Draw%, p1 win% and game length may give some indication of trends as AI strength increases; but be aware that the AI can introduce bias due to horizon effects, poor heuristics, etc.
| Size (bytes) | 24098 |
|---|---|
| Reference Size | 10293 |
| Ratio | 2.34 |
Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.
| Playouts per second | 107954.05 (9.26µs/playout) |
|---|---|
| Reference Size | 387717.12 (2.58µs/playout) |
| Ratio (low is good) | 3.59 |
Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.
| 1: Odd win % | 49.60±3.09 | Includes draws = 50% |
|---|---|---|
| 2: Even win % | 50.40±3.09 | Includes draws = 50% |
| Draw % | 0.00 | Percentage of games where all players draw. |
| Decisive % | 100.00 | Percentage of games with a single winner. |
| Samples | 1000 | Quantity of logged games played |
Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)
Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.
| Label | Its/s | SD | Nodes/s | SD | Game length | SD |
|---|---|---|---|---|---|---|
| Random playout | 162,434 | 531 | 20,629,108 | 67,493 | 127 | 0 |
| search.UCB | 134,220 | 9,007 | 127 | 0 | ||
| search.UCT | 128,775 | 1,325 | 127 | 0 |
Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.
Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.
Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.
Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.
| Game length | 127.00 | |
|---|---|---|
| Branching factor | 128.00 | |
| Complexity | 10^251.71 | Based on game length and branching factor |
| Computational Complexity | 10^8.71 | Sample quality (100 best): 0.32 |
| Samples | 1000 | Quantity of logged games played |
| Distinct actions | 254 | Number of distinct moves (e.g. "e4") regardless of position in game tree |
|---|---|---|
| Good moves | 121 | A good move is selected by the AI more than the average |
| Bad moves | 133 | A bad move is selected by the AI less than the average |
| Samples | 1000 | Quantity of logged games played |

This chart is based on a single playout, and gives a feel for the change in material over the course of a game.
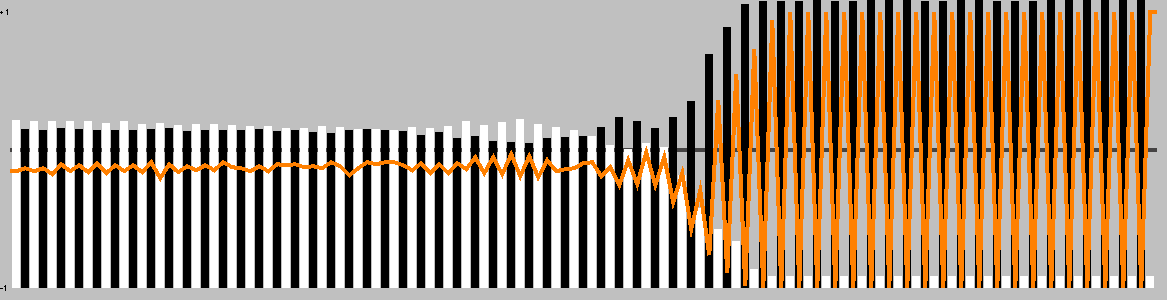
This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).
The lead changed on 46% of the game turns. Ai Ai found 3 critical turns (turns with only one good option).
Overall, this playout was 74.80% hot.

This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).
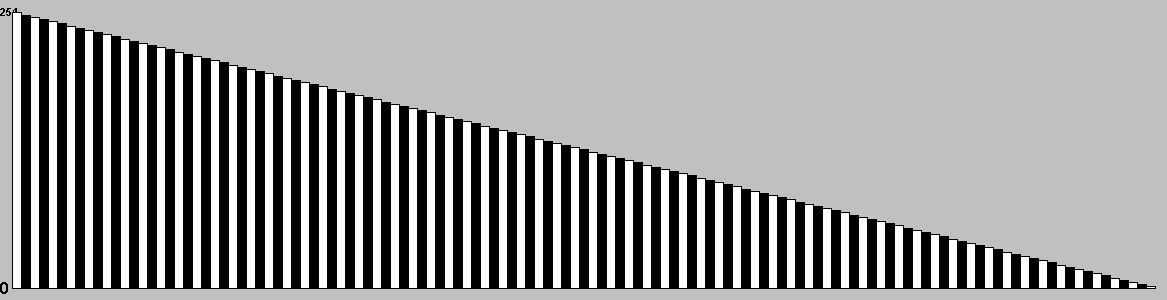
Table: branching factor per turn.
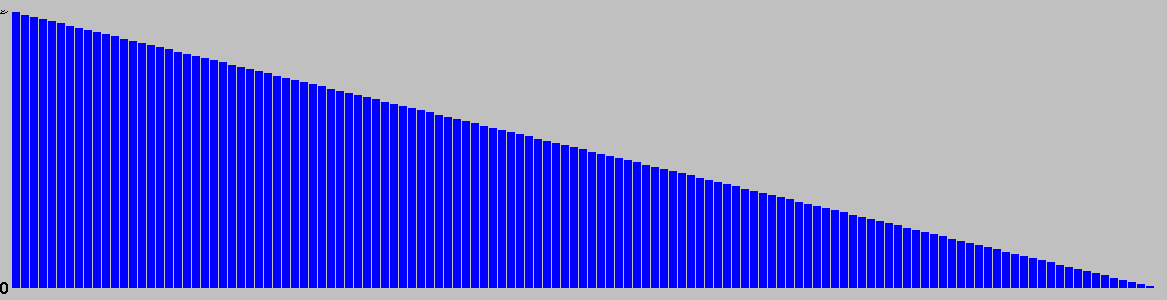
This chart is based on a single playout, and gives a feel for the types of moves available over the course of a game.
Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.
| 0 | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 254 | 32258 | 2699258 |
Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.
No solutions found to depth 3.
| Puzzle | Solution |
|---|---|
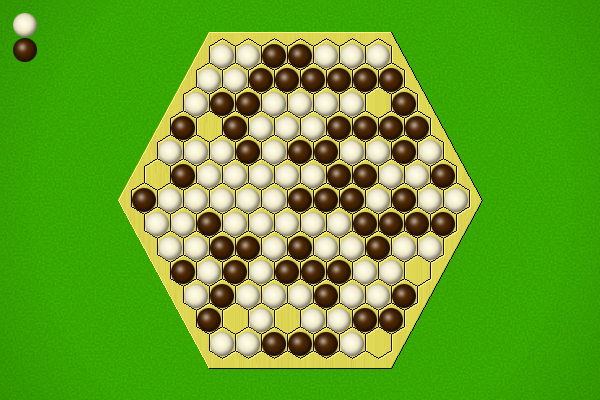 Odd to win in 7 moves |
Selection criteria: first move must be unique, and not forced to avoid losing. Beyond that, Puzzles will be rated by the product of [total move]/[best moves] at each step, and the best puzzles selected.