Full Report for Othellito by Jonas Lidström Isegrim

Rules

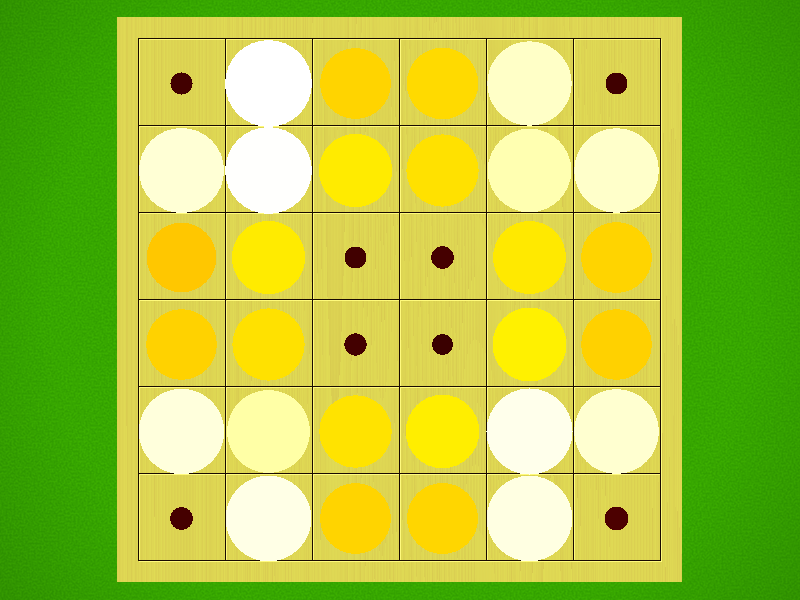
Start Position

The grid

The four by four (4x4) invisible and floating grid is formed by the cards placed and may shift during play. Players must place their card adjacent next to another card on the board, orthogonally or diagonally.

Play

Players (starting with black) take turns, placing cards of their assigned colour on the board. During a play, any cards of the opponent's colour that are in a straight line and bounded by the card just placed and another card of the current player's colour are turned over to the current player's colour.

Each turn, you must flip at least one card.

Clear a column or row

If you place a card so there is a fifth row or column, you must remove the opposite row or column; however, you may not remove a row or column containing more cards than you just flipped. If you cannot do so, the play is illegal.

Goal

The game ends when a player has no legal moves.

The player with most of their own colour facing up wins. Ties are possible.

Miscellaneous

General comments:

Play: Combinatorial

Family: Combinatorial 2019,Minimal

Mechanism(s): No Board,Scoring

Level: Standard

BGG Stats

BGG Ratings and Comments

Kolomogorov Complexity Estimate

Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.

Playout Complexity Estimate

Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.

Playout/Search Speed

Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.

Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.

Mirroring Strategies

Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.

Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.

Win % By Player (Bias)

Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)

Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.

Levels of Play

Level of Play: Strong beats Weak 60% of the time (lower bound with 90% confidence).

Draw%, p1 win% and game length may give some indication of trends as AI strength increases; but be aware that the AI can introduce bias due to horizon effects, poor heuristics, etc.

Complexity

Computational complexity (where present) is an estimate of the game tree reachable through actual play. For each game in turn, Ai Ai marks the positions reached in a hashtable, then counts the number of new moves added to the table. Once all moves are applied, it treats this sequence as a geometric progression and calculates the sum as n-> infinity.

Move Classification

Board Coverage

A mean of 65.55% of board locations were used per game.

Colour shows the frequency of visits.

Change in Material Per Turn

This chart is based on a single playout, and gives a feel for the change in material over the course of a game.

Actions/turn

Table: branching factor per turn.

Action Types per Turn

This chart is based on a single playout, and gives a feel for the types of moves available over the course of a game.

Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.

Trajectory

This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).

The lead changed on 44% of the game turns. Ai Ai found 36 critical turns (turns with only one good option).

Position Heatmap

This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).

Good/Effective moves

These figures were calculated over a single game.

An effective move is one with score 0.1 of the best move (including the best move). -1 (loss) <= score <= 1 (win)

A good move has a score > 0. Note that when there are no good moves, an multiplier of 1 is used for the game space calculation.

Quality Measures

These figures were calculated over a single game, and based on the measures of quality described in "Automatic Generation and Evaluation of Recombination Games" (Cameron Browne, 2007).

Openings

Moves	Animation
d2,c2,b1,e5,c6,b1,f5,b6,a1,f5,a6
d2,e2,b4,b5,c5,b3,a5,b6,e1,f2
d2,e2,c5,b5,b4,b3,a5,b6,e1,f2
e3,e2,b4,b5,b6,a5,f2,a3,a3,f2
b4,b5,d2,e2,c5,b3,a5,b6,e1,f2
b4,b5,e3,e2,b6,a5,f2,a3,a3,f2
c5,b5,d2,e2,b4,b3,a5,b6,e1,f2
d2,c2,b1,e5,c6,b1,f5,b6,a1,f5
e3,c2,b4,f3,b1,a4,e3,e2,f4,d5
e3,c2,b5,f3,b1,a4,e3,e2,f4,d5
e3,e2,b4,b5,c5,d5,b6,a5,f2,e1
e3,e2,b4,b5,b6,a5,d4,e4,f2,e1

Opening Heatmap

Colour shows the success ratio of this play over the first 10moves; black < red < yellow < white.

Size shows the frequency this move is played.

Unique Positions Reachable at Depth

Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.

Shortest Game(s)

10 solutions found at depth 6.

Puzzles

Puzzle	Solution
White to win in 10 moves	Show Solution
White to win in 5 moves	Show Solution

Selection criteria: first move must be unique, and not forced to avoid losing. Beyond that, Puzzles will be rated by the product of [total move]/[best moves] at each step, and the best puzzles selected.