Full Report for Peak by Andreas Kuhnekath

Rules

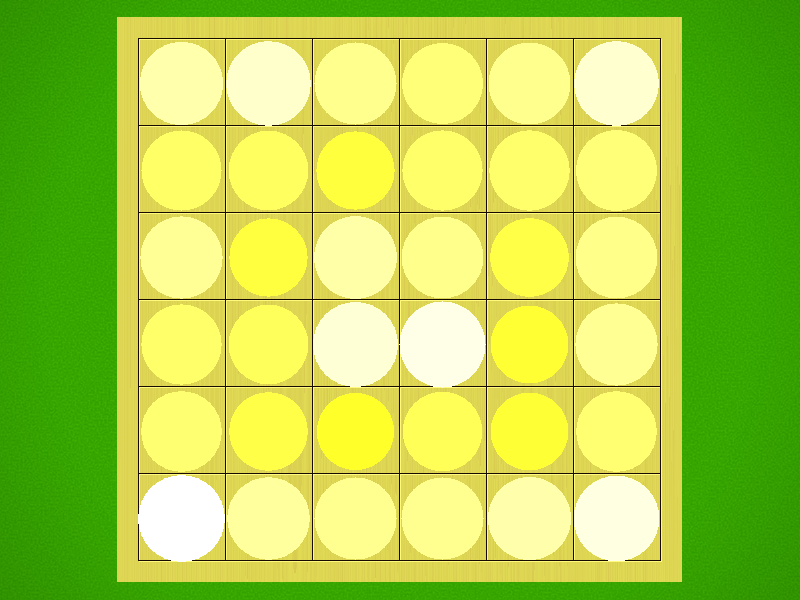
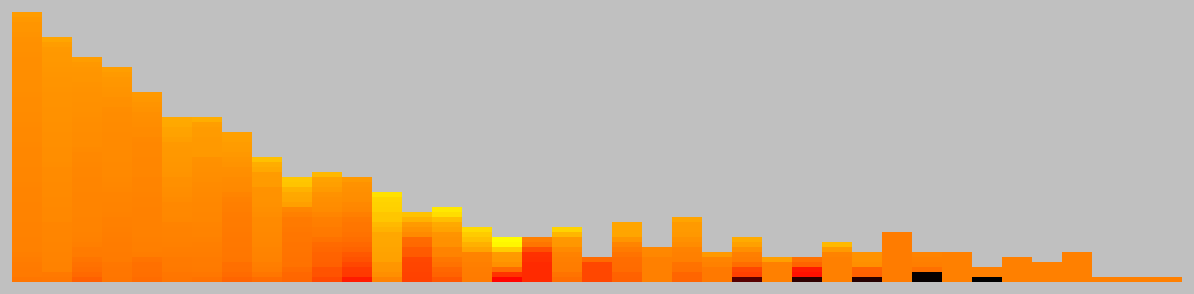
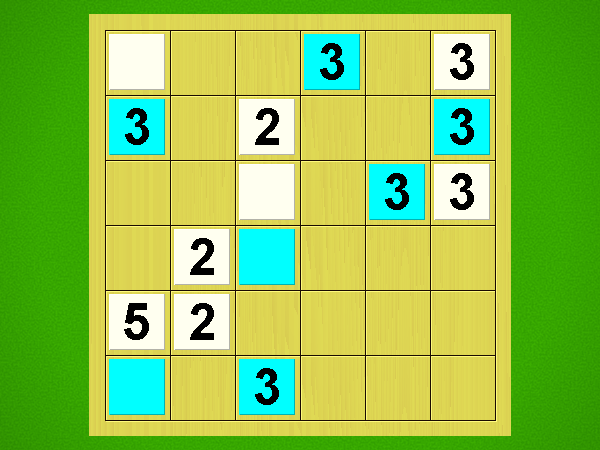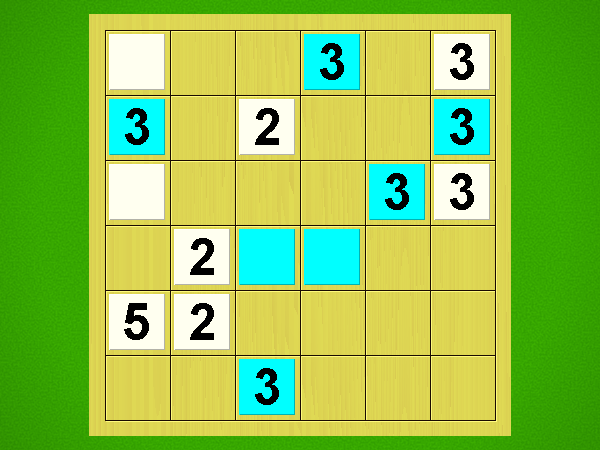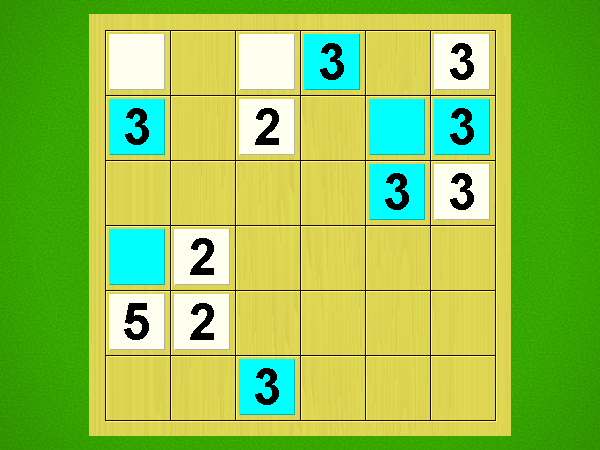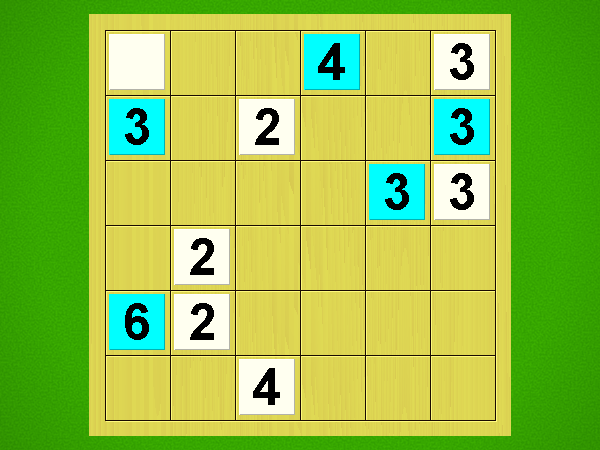
Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!

Object of the game

The player who stacks best and is thus able to claim the most pieces wins the game. The top piece of each tower is what's crucial!

This is how you play

Players alternate turns; the player with the light-colored playing pieces begins the game.

On your turn, you may only jump with one of your playing pieces; sliding a piece is not allowed. A jump always goes over exactly 2 other playing pieces, orthogonally or diagonally, onto a space behind that. You may jump over any number of unoccupied spaces; they are not included in the count.

The jumped-over playing pieces may lie on the board next to one another, on top of each other, or with a distance between them - all options are possible; only the number TWO has to be exact.

End of the game

Once one player can no longer jump, the other player has another turn. If that first player now has another possibility to jump, the game goes on. But if he still can't jump, then the game ends.

Scoring

Only towers that consist of at least 2 stacked playing pieces are scored. Single playing pieces are removed from the game.

Each player scores for the towers with his color on top. He adds up all the playing pieces of his towers; each piece is worth one point. Who will have the most points in the end?

Miscellaneous

General comments:

Play: Combinatorial

Family: Combinatorial 2021

Mechanism(s): Capture,Movement,Stacking

BGG Stats

BGG Entry	Peak
BGG Rating	7.84615
#Voters	13
SD	1.09868
BGG Weight	0
#Voters	0
Year	2021

BGG Ratings and Comments

User	Rating	Comment
getareaction	8	Bought in October 2021. Aesthetically wonderful, beautifully simple rules, interesting decision space, not immediately obvious how to play well. I like it.
jakob1983	8
pecan	7	https://twitter.com/pecan7uts/status/1497397463585812480?s=20&t=aMbLm5cUAdRaUrn88RFF2Q https://twitter.com/pecan7uts/status/1497537797393371136?s=20&t=aMbLm5cUAdRaUrn88RFF2Q Fun. I guess it's rare to jump 2 pieces in a turn instead of 2 spaces. I like the rules of this game except there are no tie breakers.
Tolkana	8
r0cka	8
gabeschw	8
S.K. Lator	8	Quick strategic fun. Easy to overlook crucial moving options of your opponent. Another winner from Andreas Kuhnekath.
Pfahrer	7
gubo	9
iMisut	8
JayStay	5
rocket boy	10
Thesp	8	Very clever game with super-easy rule set with a lot of depth.

Kolomogorov Complexity Analysis

Size (bytes)	27635
Reference Size	10673
Ratio	2.59

Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.

Playout Complexity Estimate

Playouts per second	34630.84 (28.88µs/playout)
Reference Size	491472.94 (2.03µs/playout)
Ratio (low is good)	14.19

Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.

State Space Complexity

% new positions/bucket

State Space Complexity	547998573
State Space Complexity bounds	62376009 < 547998573 < ∞
State Space Complexity (log 10)	8.74
State Space Complexity bounds (log 10)	7.80 <= 8.74 <= ∞
Samples	1138817
Confidence	0.00	0: totally unreliable, 100: perfect

State space complexity (where present) is an estimate of the number of distinct game tree reachable through actual play. Over a series of random games, Ai Ai checks each position to see if it is new, or a repeat of a previous position and keeps a total for each game. As the number of games increase, the quantity of new positions seen per game decreases. These games are then partitioned into a number of buckets, and if certain conditions are met, Ai Ai treats the number in each bucket as the start of a strictly decreasing geometric sequence and sums it to estimate the total state space. The accuracy is calculated as 1-[end bucket count]/[starting bucklet count]

Playout/Search Speed

Label	Its/s	SD	Nodes/s	SD	Game length	SD
Random playout	40,044	650	1,242,697	20,173	31	6
search.UCT	44,082	3,832			41	15

Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.

Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.

Mirroring Strategies

Rotation (Half turn) drew against Grand Unified UCT(U1-T,rSel=s, secs=1.00) playing 2nd, moves: [c1-c4, d6-d3, e4-c2, b3-d5, c5-f2, d2-a5, e6-e2, b1-b5, a2-d5, f5-c2, d1-d4, c6-c3, a4-c6, f3-d1, a6-a3, f1-f4, b4-d2, e3-c5, d2-b4, c5-e3, b4-e1, e3-b6, b2-b6, e5-e1, c6-c3, d1-d4, f6-f3, a1-a4, f3-f5, a4-a2, f5-f3, a2-a4, f3-d1, a4-c6, d1-f3, c6-a4, f3-d1, a4-c6, d1-f3, c6-a4, f3-f1, a4-a6, f1-f3, a6-a4, f3-f5, a4-a2, f5-f3, a2-a4, f3-f1, a4-a6, f1-f3, a6-a4, f3-d1, a4-c6, d1-f3, c6-a4, f3-f5, a4-a2, f5-f3, a2-a4, f3-f5, a4-a2, f5-f3, a2-a4, f3-f5, a4-a2, f5-c2, a2-d5, Pass, Pass, Pass]
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.

Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.

Win % By Player (Bias)

1: White win %	55.80±3.09	Includes draws = 50%
2: Blue win %	44.20±3.05	Includes draws = 50%
Draw %	9.40	Percentage of games where all players draw.
Decisive %	90.60	Percentage of games with a single winner.
Samples	1000	Quantity of logged games played

Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)

Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.

UCT Skill Chains

Match	AI	Strong Wins	Draws	Strong Losses	#Games	Strong Score	p1 Win%	Draw%	p2 Win%	Game Length
0	Random
1	UCT (its=2)	609	43	320	972	0.6181 <= 0.6487 <= 0.6780	47.94	4.42	47.63	30.56
5	UCT (its=6)	605	51	292	948	0.6344 <= 0.6651 <= 0.6944	47.89	5.38	46.73	30.66
16	UCT (its=17)	604	54	333	991	0.6063 <= 0.6367 <= 0.6661	46.12	5.45	48.44	29.52
39	UCT (its=40)	605	51	327	983	0.6109 <= 0.6414 <= 0.6708	46.29	5.19	48.52	29.04
54	UCT (its=147)	608	46	268	922	0.6537 <= 0.6844 <= 0.7136	46.96	4.99	48.05	28.98
55	UCT (its=399)	607	47	288	942	0.6386 <= 0.6693 <= 0.6986	46.28	4.99	48.73	29.53
56	UCT (its=1085)	599	64	288	951	0.6329 <= 0.6635 <= 0.6928	45.32	6.73	47.95	31.69
57	UCT (its=2948)	607	48	273	928	0.6493 <= 0.6800 <= 0.7092	48.38	5.17	46.44	33.43
58	UCT (its=8014)	600	61	279	940	0.6401 <= 0.6707 <= 0.7000	49.26	6.49	44.26	35.69
59	UCT (its=8014)	433	87	480	1000	0.4457 <= 0.4765 <= 0.5075	47.60	8.70	43.70	37.69

Search for levels ended: time limit reached.

Level of Play: Strong beats Weak 60% of the time (lower bound with 95% confidence).

Draw%, p1 win% and game length may give some indication of trends as AI strength increases.

1st Player Win Ratios by Playing Strength

This chart shows the win(green)/draw(black)/loss(red) percentages, as UCT play strength increases. Note that for most games, the top playing strength show here will be distinctly below human standard.

Complexity

Game length	38.84
Branching factor	16.59
Complexity	10^37.64	Based on game length and branching factor
Samples	1000	Quantity of logged games played

Computational complexity (where present) is an estimate of the game tree reachable through actual play. For each game in turn, Ai Ai marks the positions reached in a hashtable, then counts the number of new moves added to the table. Once all moves are applied, it treats this sequence as a geometric progression and calculates the sum as n-> infinity.

Move Classification

Board Size	36	Quantity of distinct board cells
Distinct actions	361	Quantity of distinct moves (e.g. "e4") regardless of position in game tree
Good moves	211	A good move is selected by the AI more than the average
Bad moves	149	A bad move is selected by the AI less than the average
Response distance%	50.48%	Distance from move to response / maximum board distance; a low value suggests a game is tactical rather than strategic.
Samples	1000	Quantity of logged games played

Board Coverage

A mean of 95.86% of board locations were used per game.

Colour and size show the frequency of visits.

Game Length

Game length frequencies.

Mean	38.84
Mode	[35]
Median	36.0

Change in Material Per Turn

Mean change in material/round	-0.55	Complete round of play (all players)

This chart is based on a single representative* playout, and gives a feel for the change in material over the course of a game. (* Representative in the sense that it is close to the mean length.)

Actions/turn

Table: branching factor per turn, based on a single representative* game. (* Representative in the sense that it is close to the mean game length.)

Action Types per Turn

This chart is based on a single representative* game, and gives a feel for the types of moves available throughout that game. (* Representative in the sense that it is close to the mean game length.)

Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.

Trajectory

This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).

The lead changed on 10% of the game turns. Ai Ai found 4 critical turns (turns with only one good option).

Position Heatmap

This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).

Good/Effective moves

Measure	All players	Player 1	Player 2
Mean % of effective moves	39.75	36.63	43.05
Mean no. of effective moves	3.08	2.90	3.26
Effective game space	10^14.36	10^7.04	10^7.33
Mean % of good moves	30.63	58.52	1.26
Mean no. of good moves	2.77	5.10	0.32
Good move game space	10^11.58	10^10.98	10^0.60

These figures were calculated over a single game.

An effective move is one with score 0.1 of the best move (including the best move). -1 (loss) <= score <= 1 (win)

A good move has a score > 0. Note that when there are no good moves, an multiplier of 1 is used for the game space calculation.

Quality Measures

Measure	Value	Description
Hot turns	71.79%	A hot turn is one where making a move is better than doing nothing.
Momentum	20.51%	% of turns where a player improved their score.
Correction	33.33%	% of turns where the score headed back towards equality.
Depth	5.84%	Difference in evaluation between a short and long search.
Drama	0.18%	How much the winner was behind before their final victory.
Foulup Factor	43.59%	Moves that looked better than the best move after a short search.
Surprising turns	2.56%	Turns that looked bad after a short search, but good after a long one.
Last lead change	23.08%	Distance through game when the lead changed for the last time.
Decisiveness	58.97%	Distance from the result being known to the end of the game.

These figures were calculated over a single representative* game, and based on the measures of quality described in "Automatic Generation and Evaluation of Recombination Games" (Cameron Browne, 2007). (* Representative, in the sense that it is close to the mean game length.)

Openings

Moves	Animation
f2-c2,f5-c5,d3-d6,f1-f6,a4-d4,b3-f3,d5-d2,c4-e4,e6-c6,a1-a4,d1-d4
d3-d6,f5-c5,f2-c2,f1-f6,a4-d4,b3-f3,d5-d2,c4-e4,e6-c6,a1-a4,d1-d4
f2-c2,f5-c5,d3-d6,f1-f6,a4-d4,b3-f3,d5-d2,c4-e4,e6-c6,a1-a4
d3-d6,f5-c5,f2-c2,f1-f6,a4-d4,b3-f3,d5-d2,c4-e4,e6-c6,a1-a4
f2-c2,f5-c5,d3-d6,f1-f6,a4-d4,b3-f3,d5-d2,c4-e4,e6-c6
d3-d6,f5-c5,f2-c2,f1-f6,a4-d4,b3-f3,d5-d2,c4-e4,e6-c6
f2-c2,f5-c5,d3-d6,f1-f6,a4-d4,b3-f3,d5-d2,c4-e4
d3-d6,f5-c5,f2-c2,f1-f6,a4-d4,b3-f3,d5-d2,c4-e4
f2-c2,f5-c5,d3-d6,f1-f6,a4-d4,b3-f3,d5-d2
d3-d6,f5-c5,f2-c2,f1-f6,a4-d4,b3-f3,d5-d2
f2-c2,f5-c5,d3-d6,f1-f6,a4-d4,b3-f3
d3-d6,f5-c5,f2-c2,f1-f6,a4-d4,b3-f3

Opening Heatmap

Colour shows the success ratio of this play over the first 10moves; black < red < yellow < white.

Size shows the frequency this move is played.

Unique Positions Reachable at Depth

0	1	2	3	4
1	54	2780	97724	3116038

Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.

Shortest Game(s)

No solutions found to depth 4.

Puzzles

Puzzle	Solution
Blue to win in 36 moves
White to win in 26 moves
White to win in 18 moves
Blue to win in 19 moves
White to win in 19 moves
White to win in 11 moves
Blue to win in 12 moves
Blue to win in 11 moves
White to win in 6 moves
Blue to win in 12 moves
White to win in 15 moves
Blue to win in 4 moves

Selection criteria: first move must be unique, and not forced to avoid losing. Beyond that, Puzzles will be rated by the product of [total move]/[best moves] at each step, and the best puzzles selected.