Full Report for Pentagame by Jan Suchanek

Pentagame is an abstract strategy game without chance element. It is played on a pentagram star that shows 100 round stops. The 5 corners and the 5 crossings in the pentagram are colored (white, blue, red, green, yellow). It can be played with 2, 3 or 4 players. It looks a bit like a pentagonal ludo, but it is truly different. For example, there is no chance and pieces don't get beaten. Instead, it is all about moving, swapping, about paths and about areas.

Rules

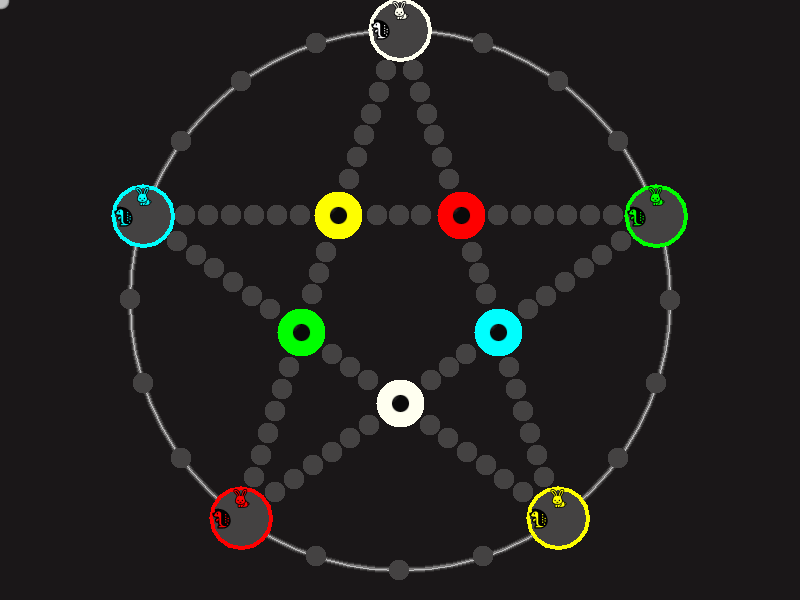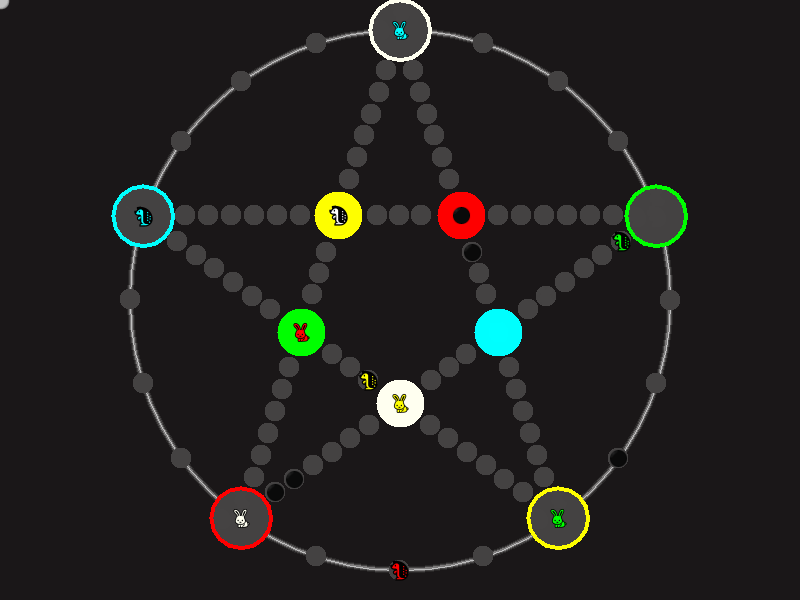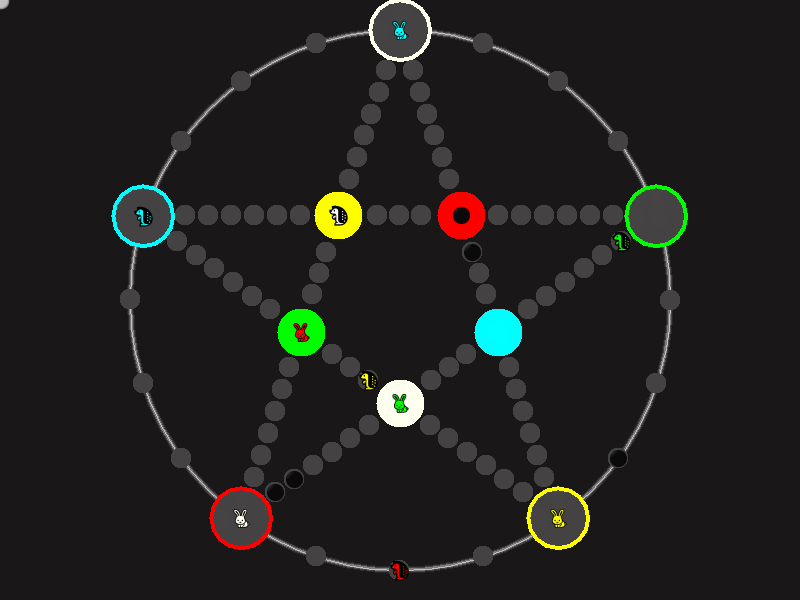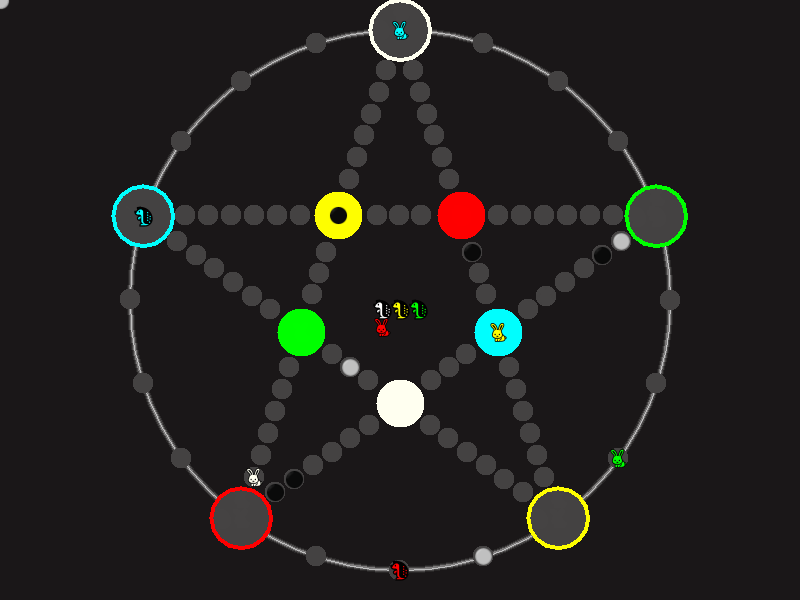
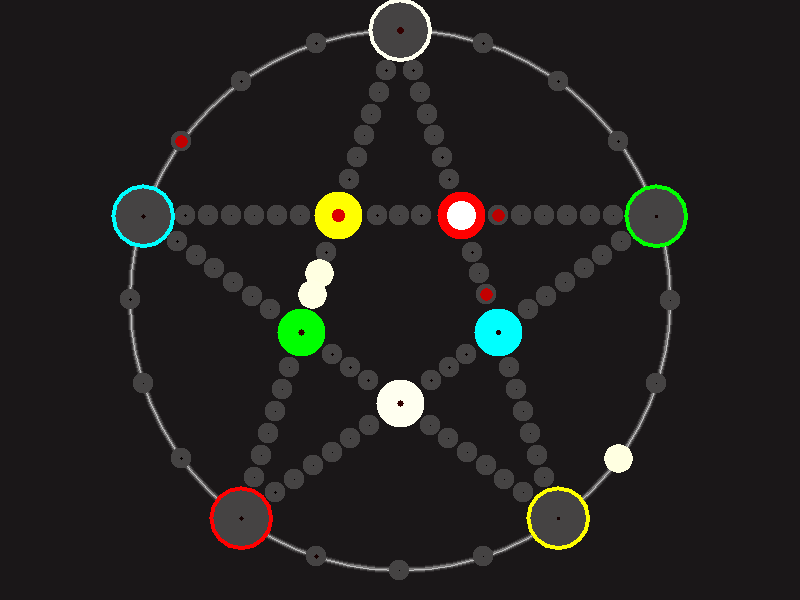
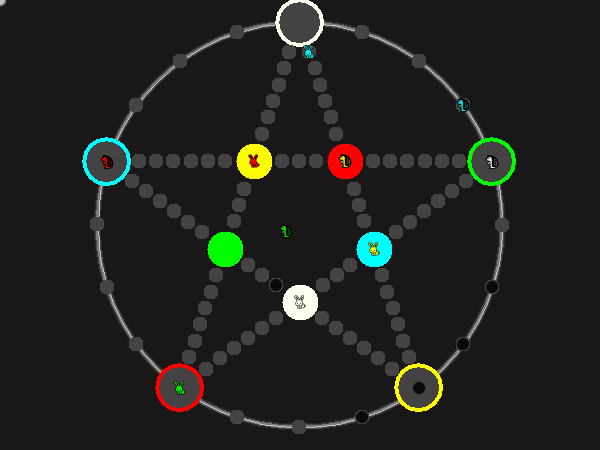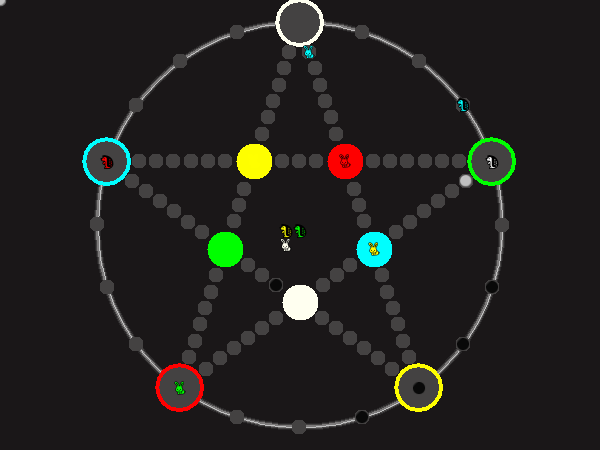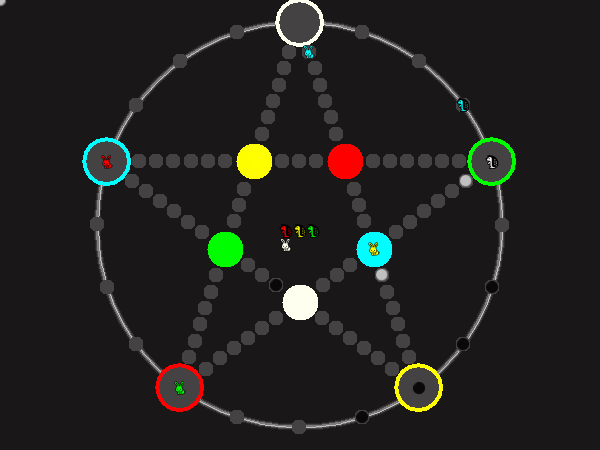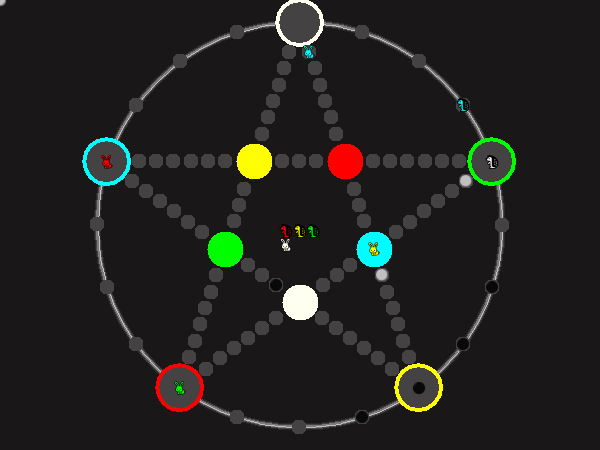
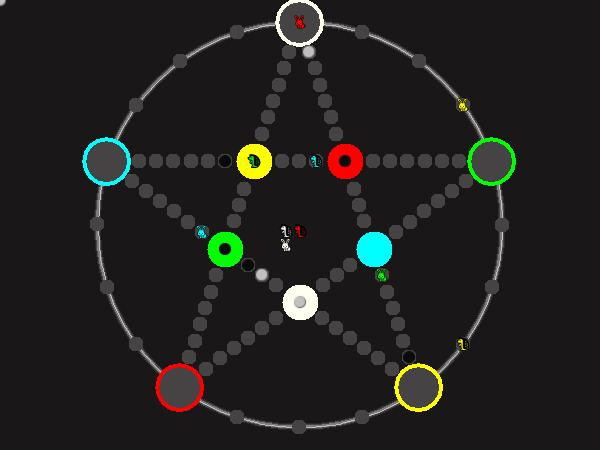
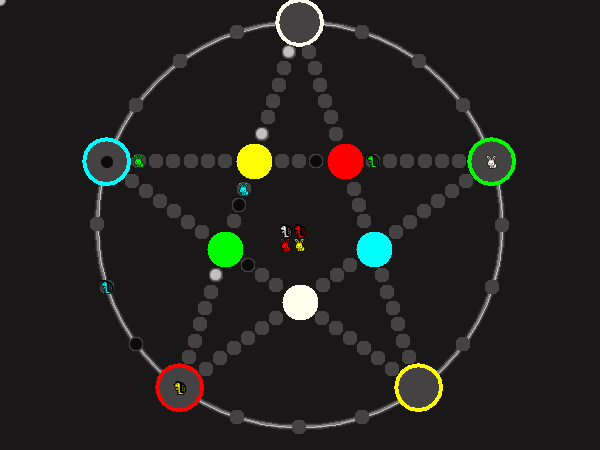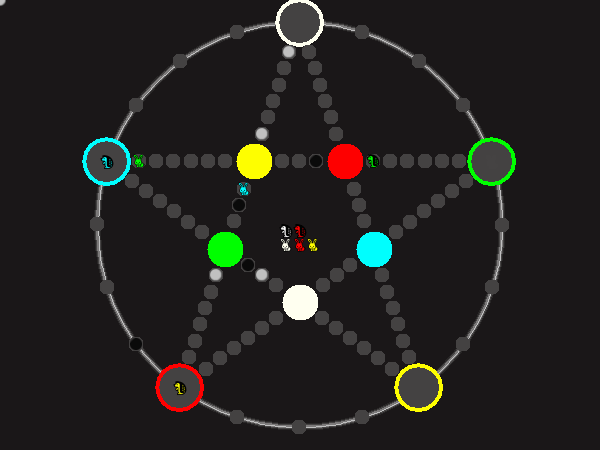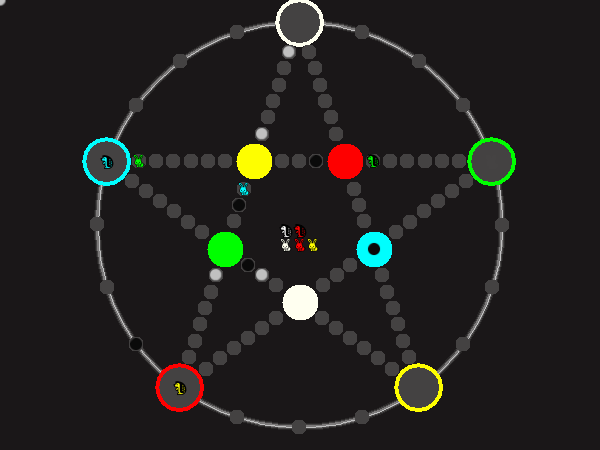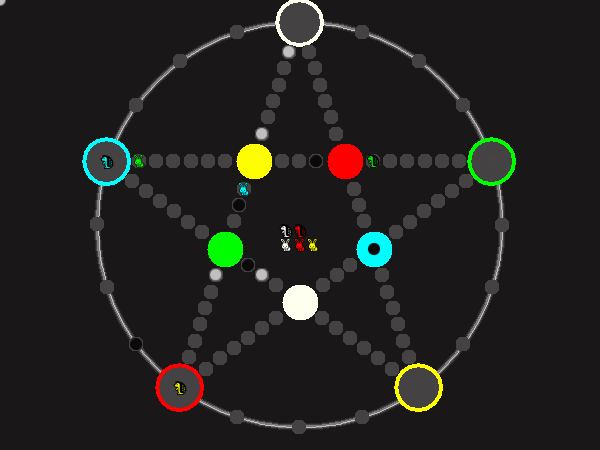
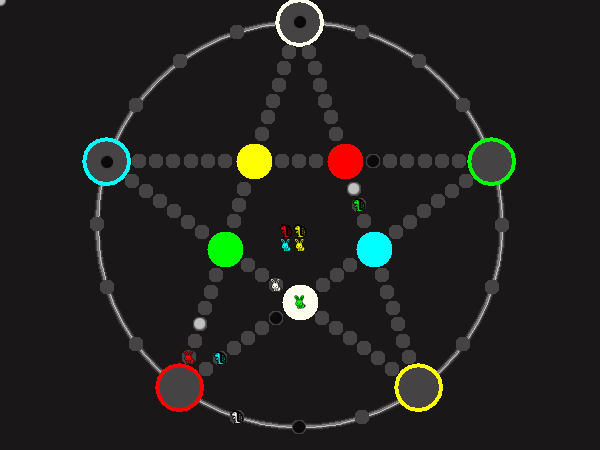
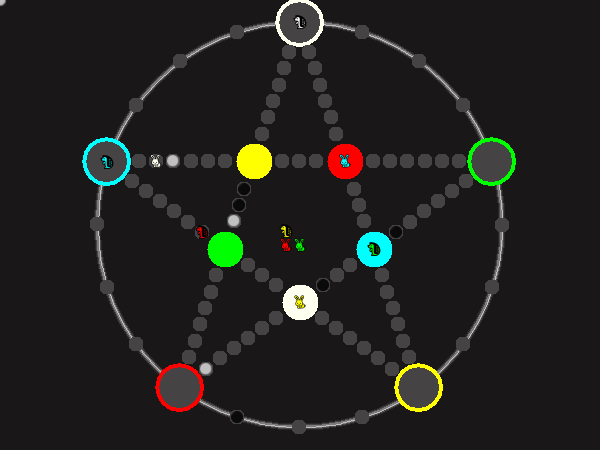
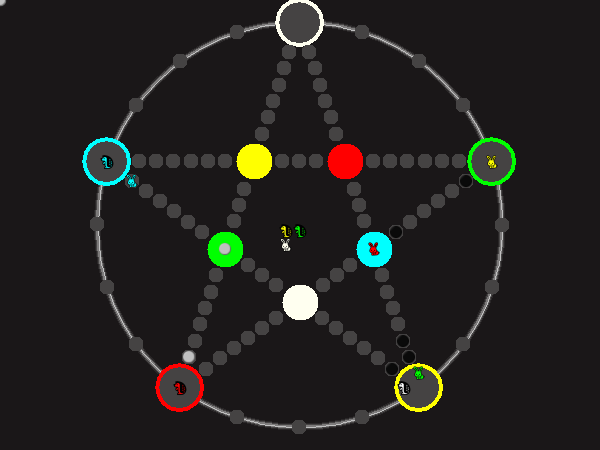
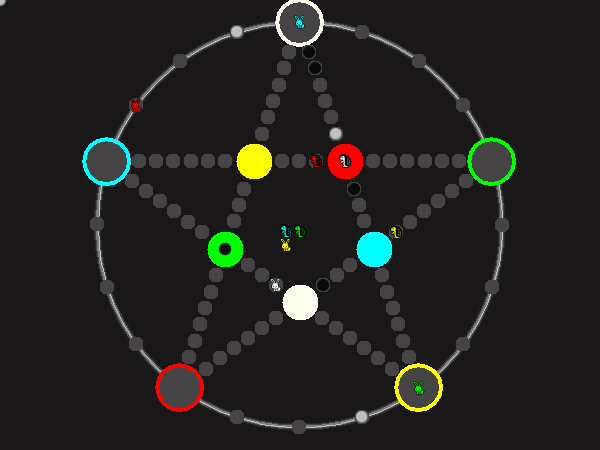
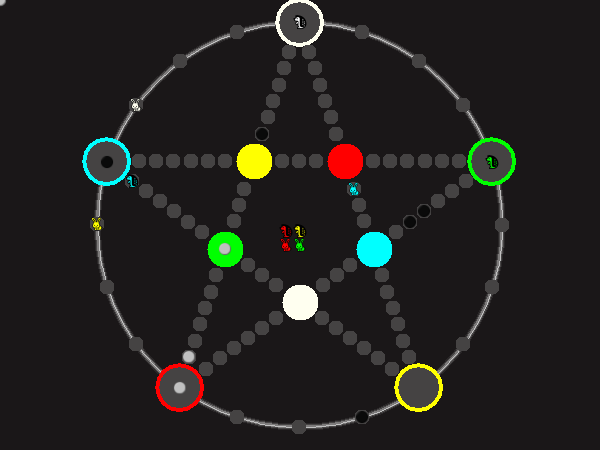
Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!

Click here for official rules in 16 languages.

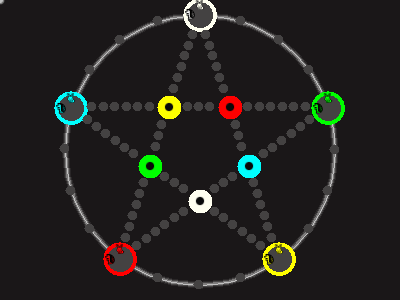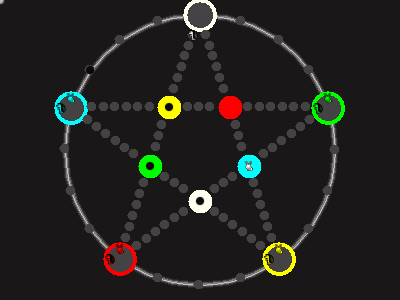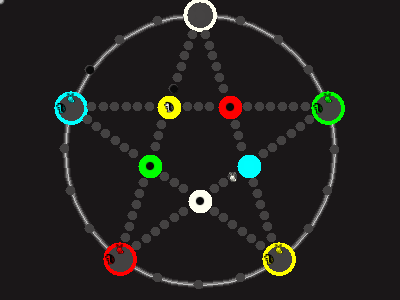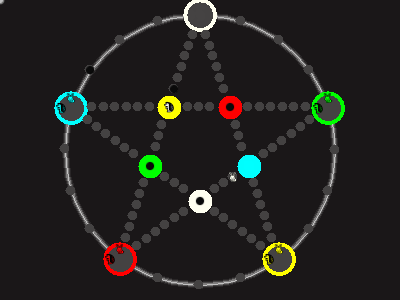
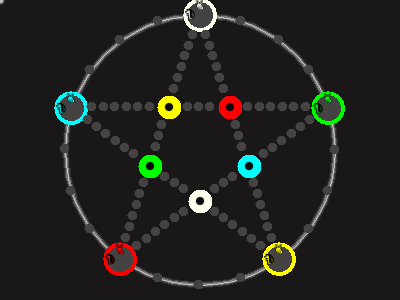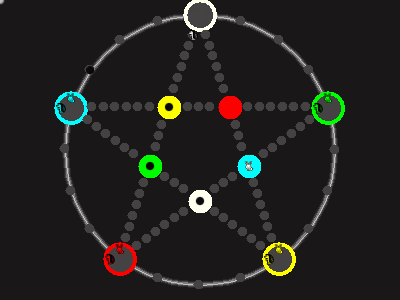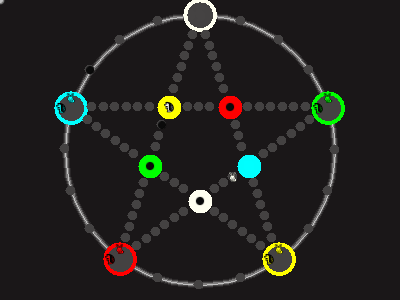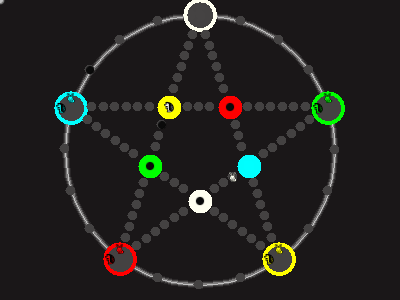
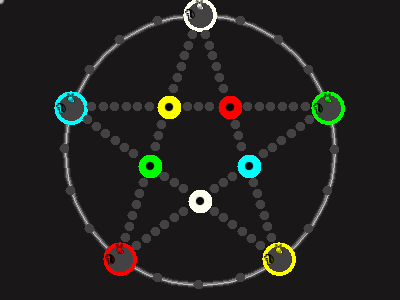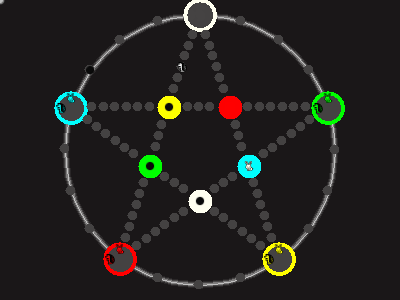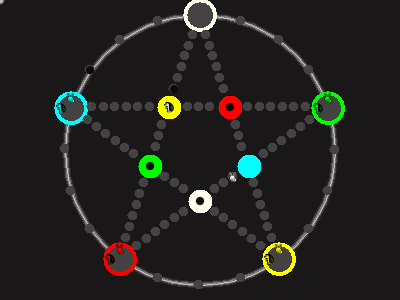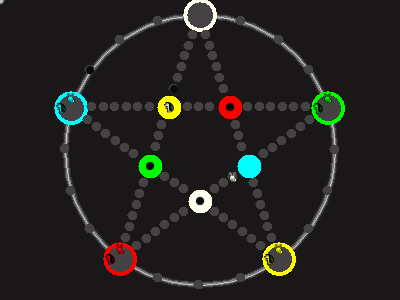
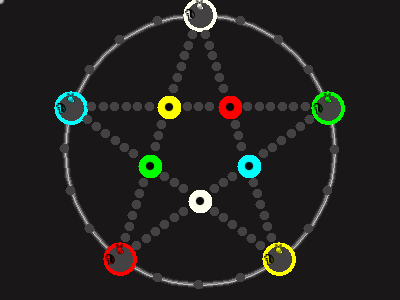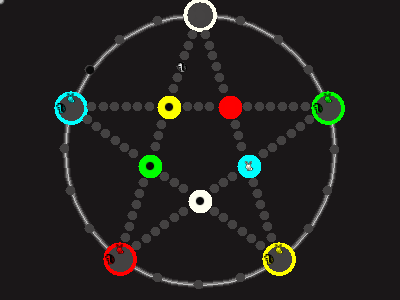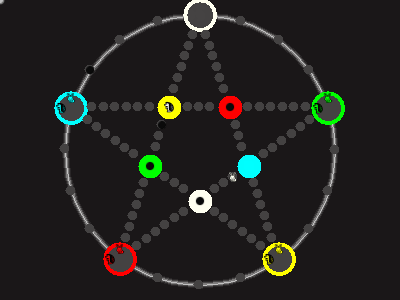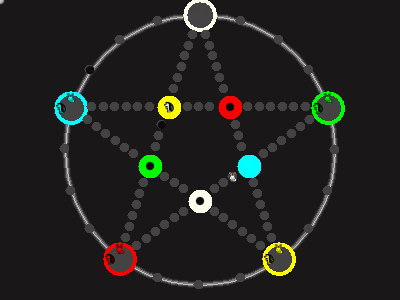
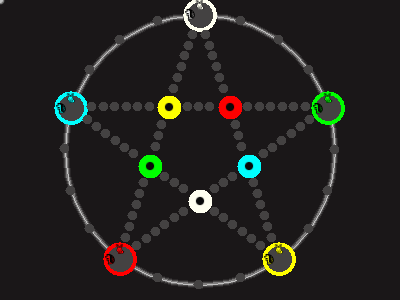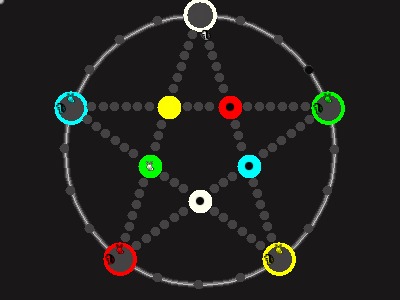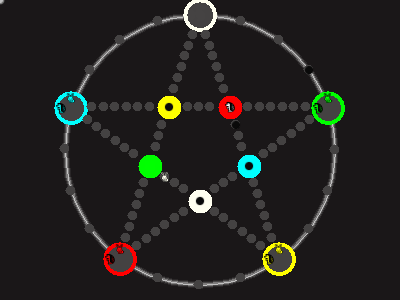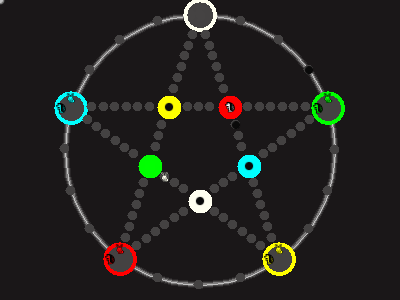
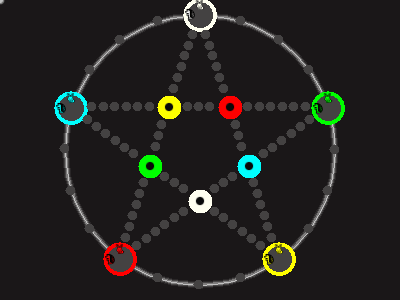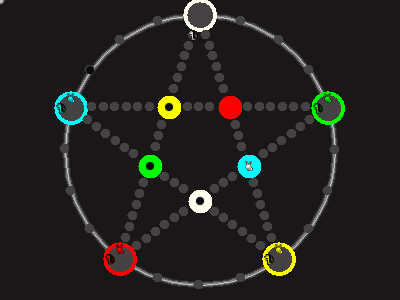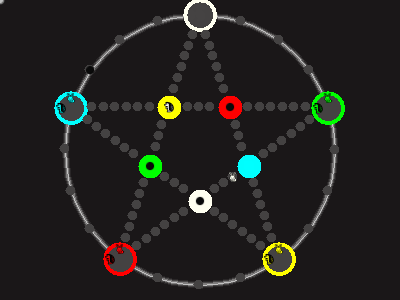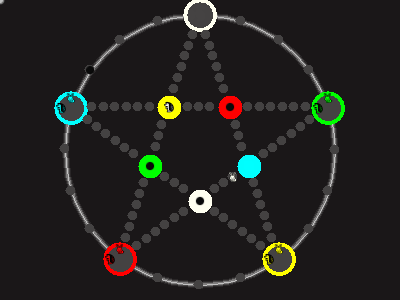
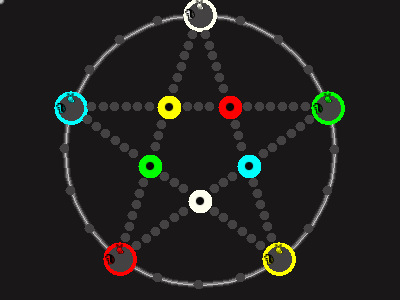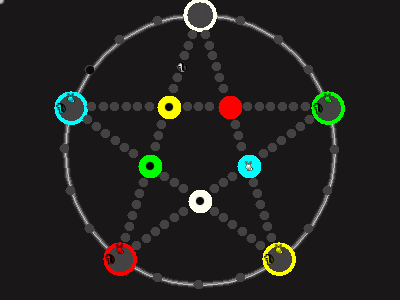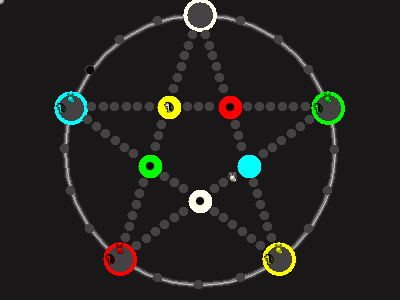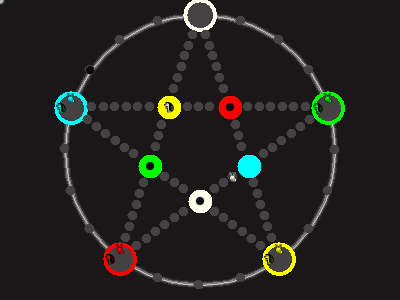
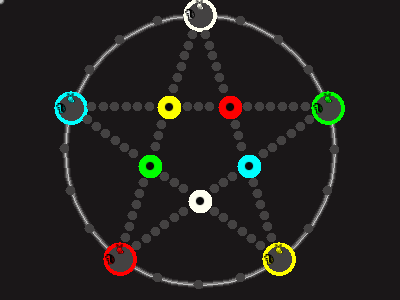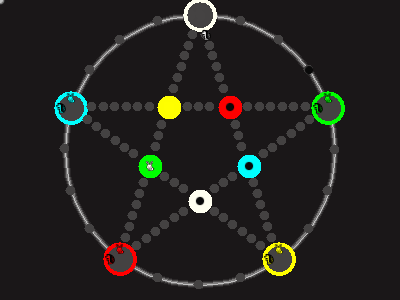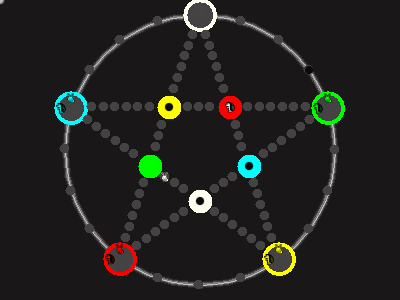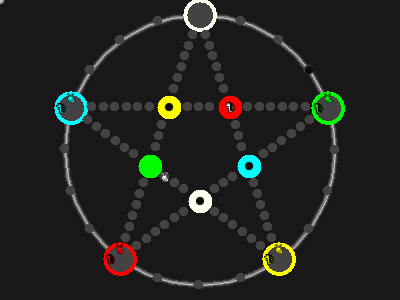
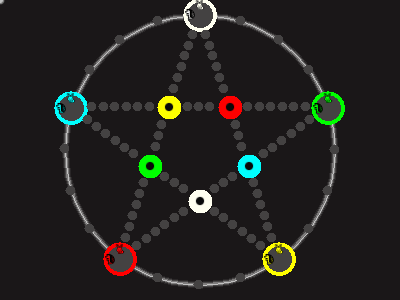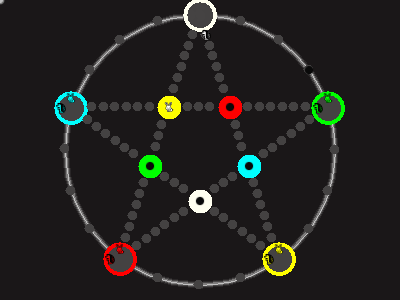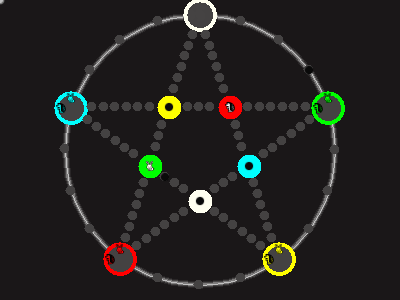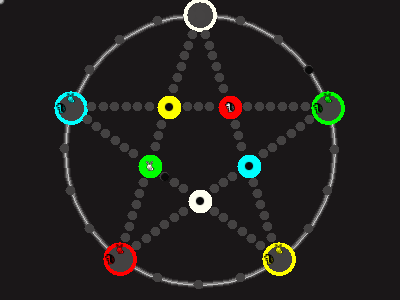
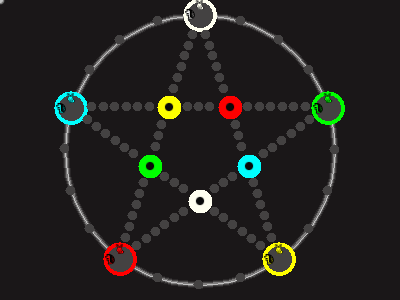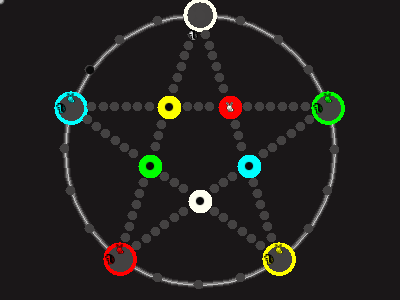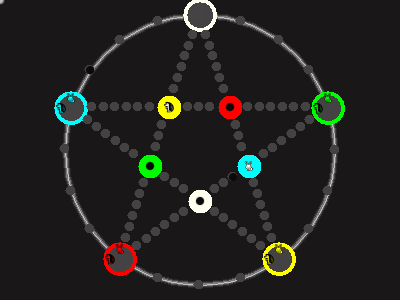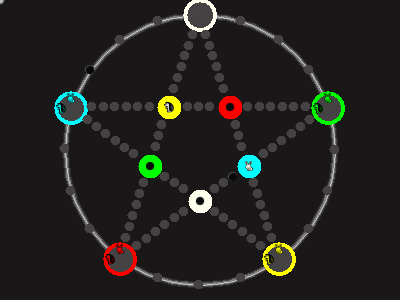
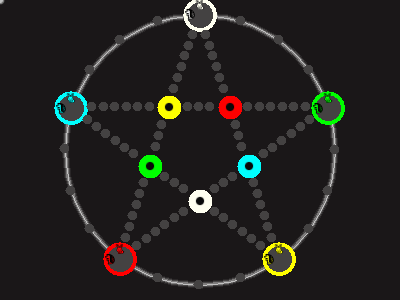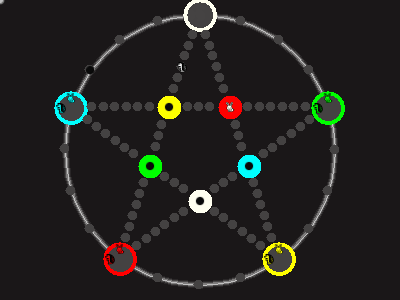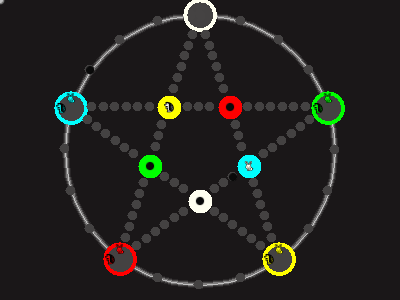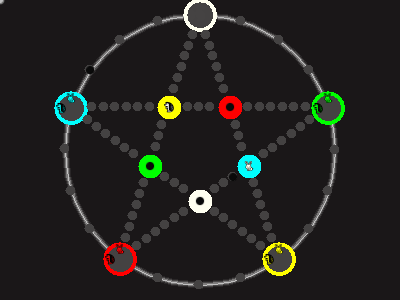
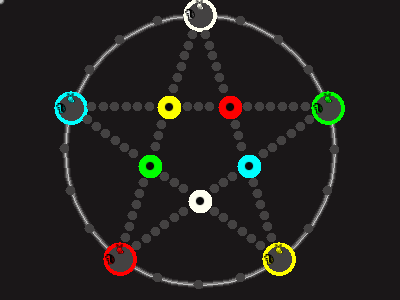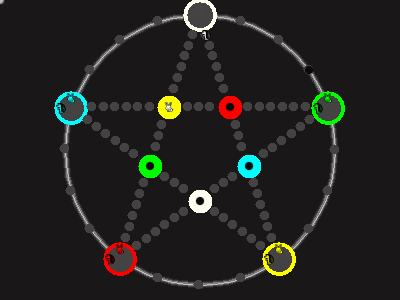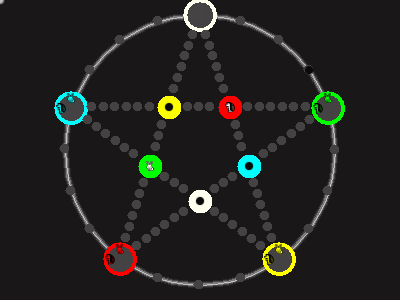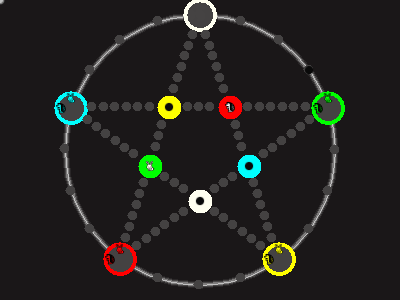
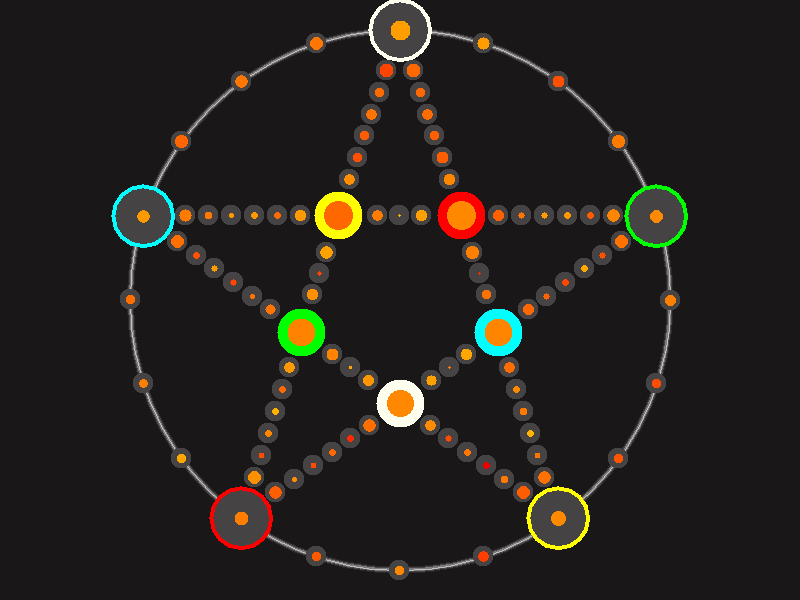
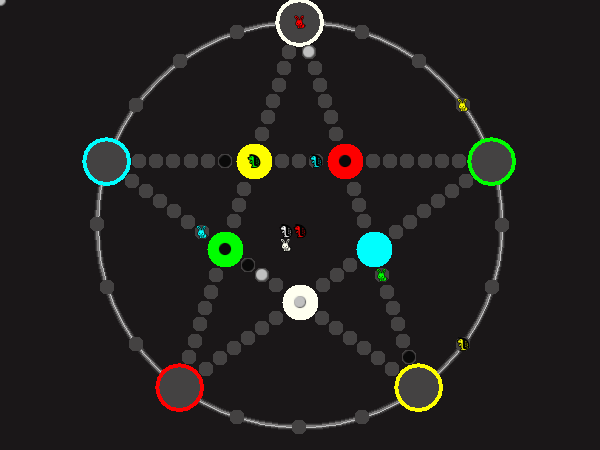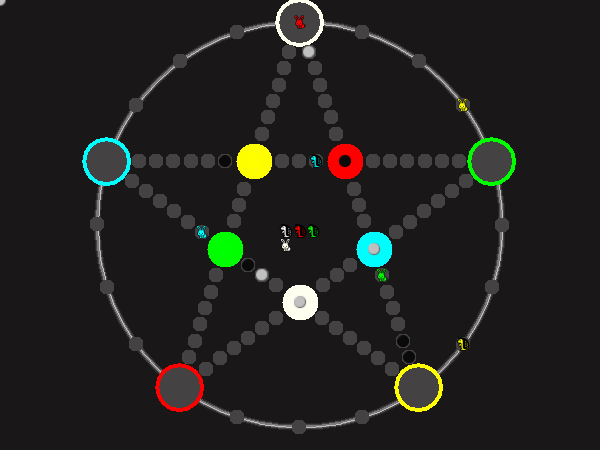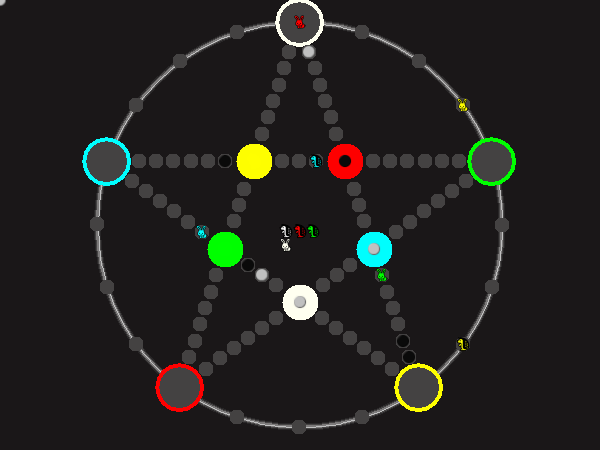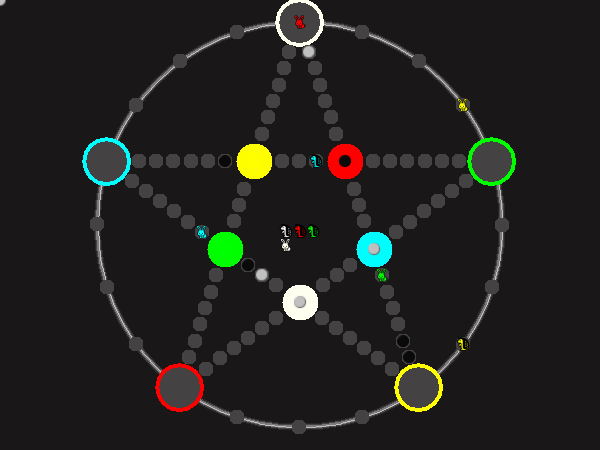
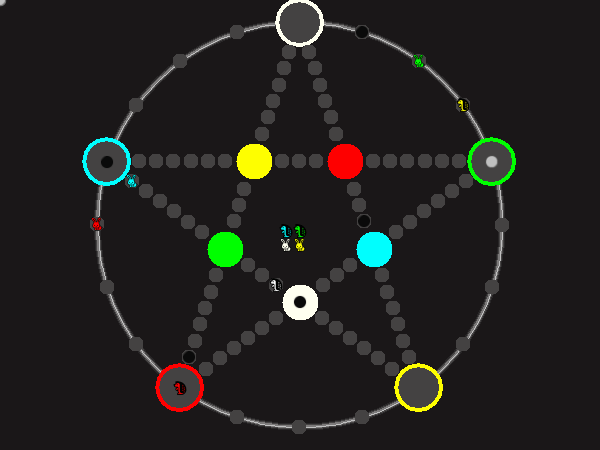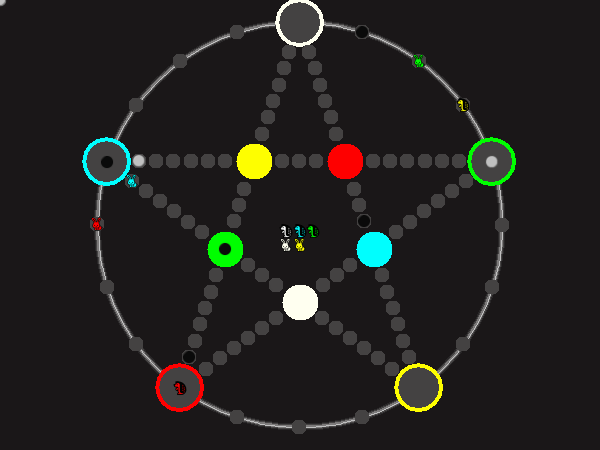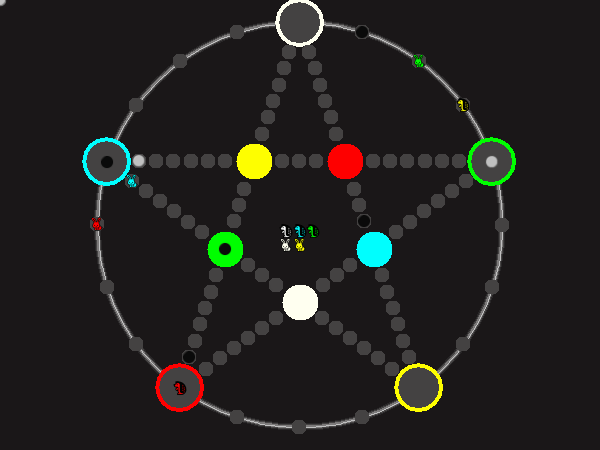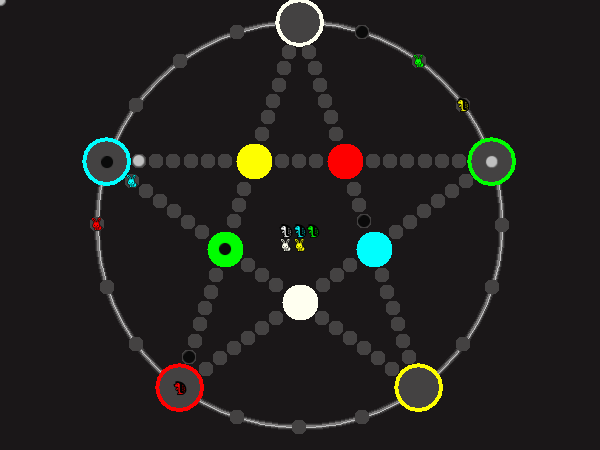
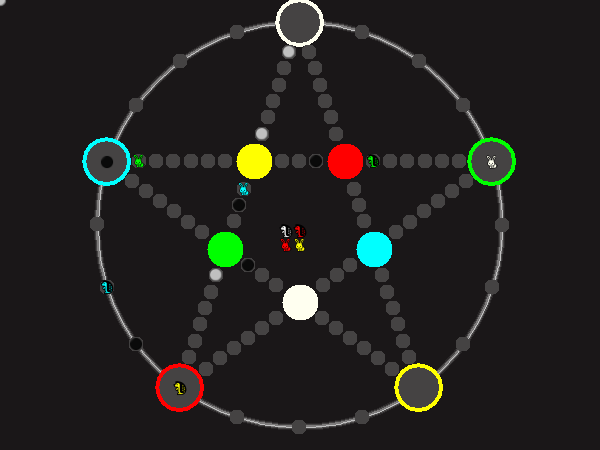
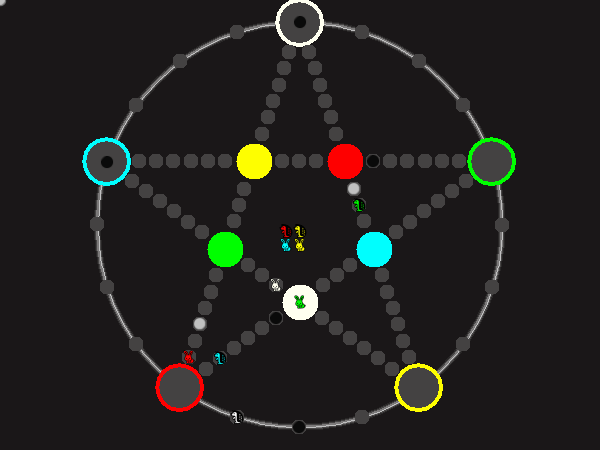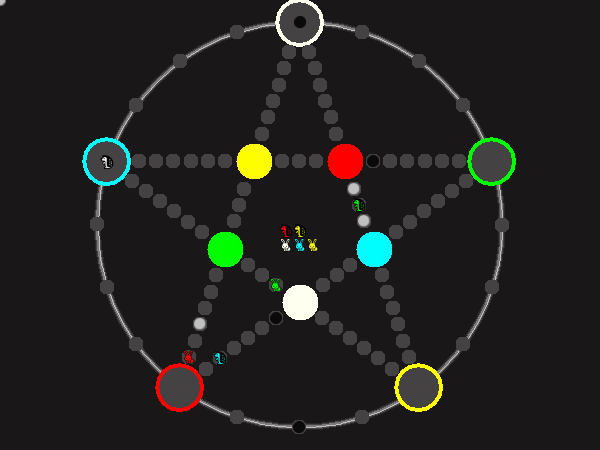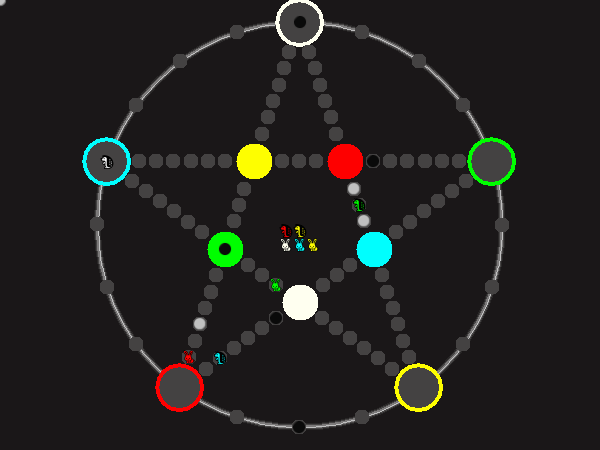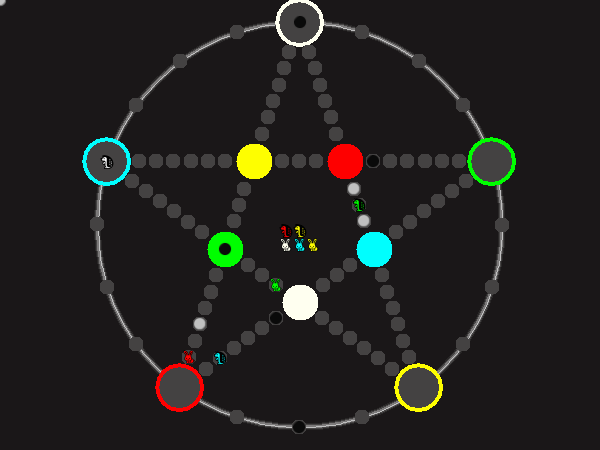
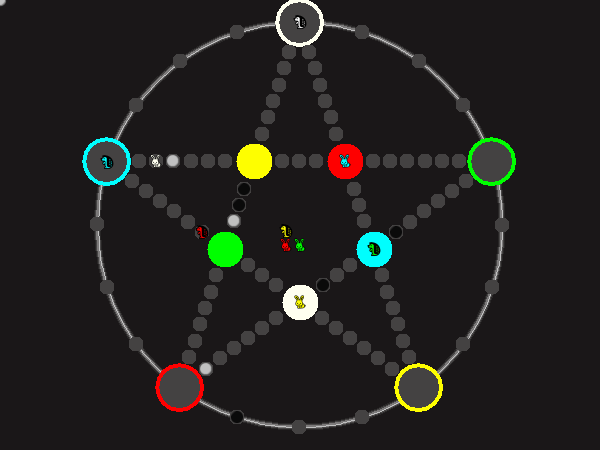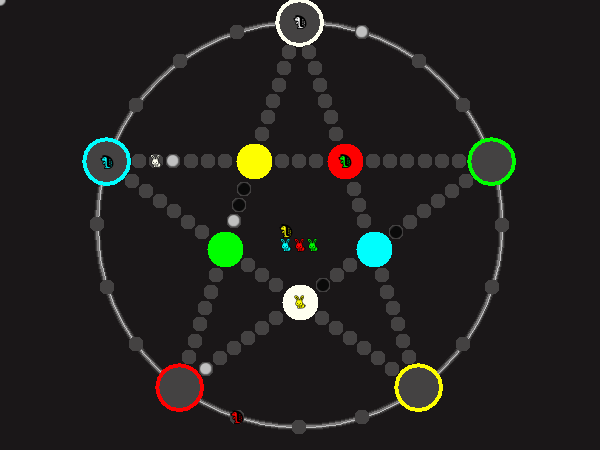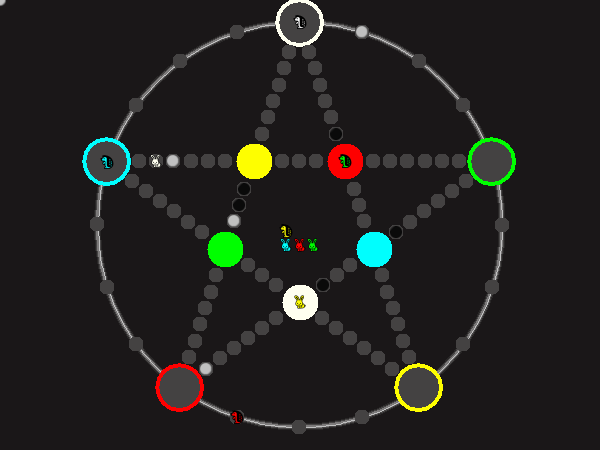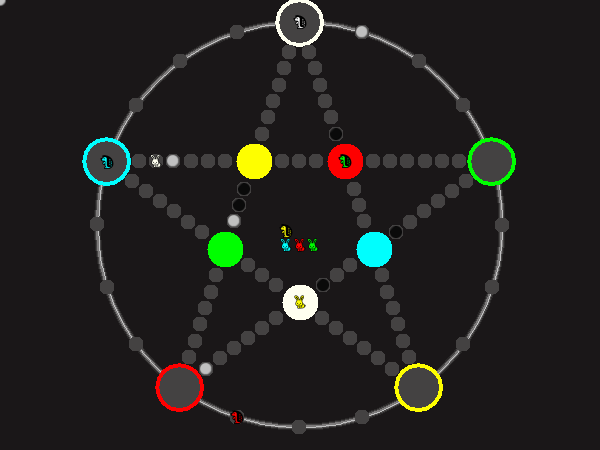
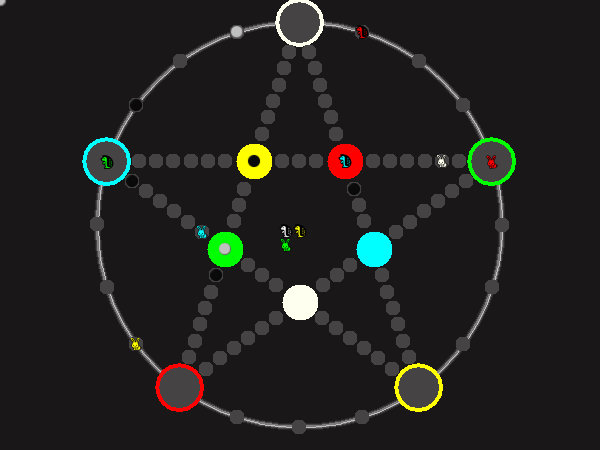
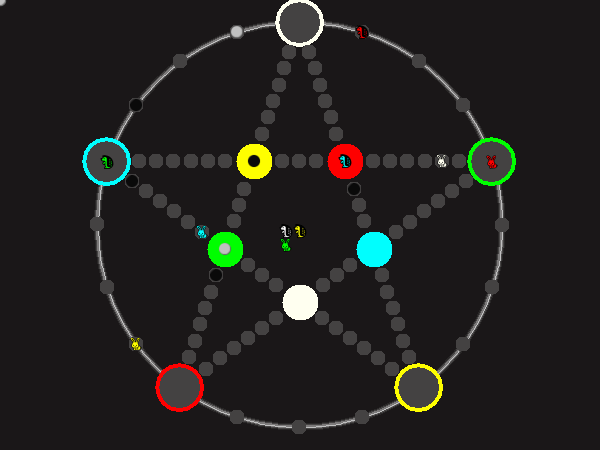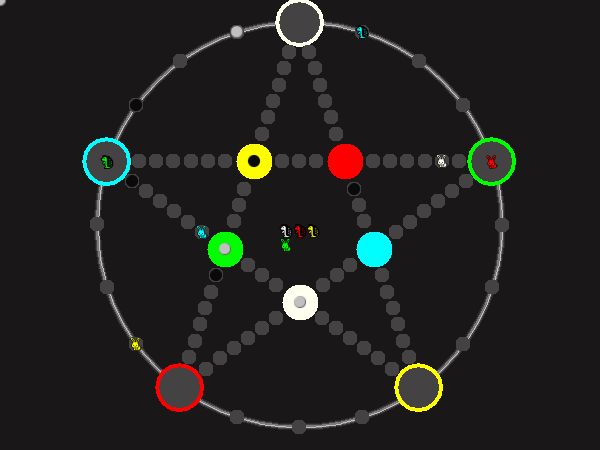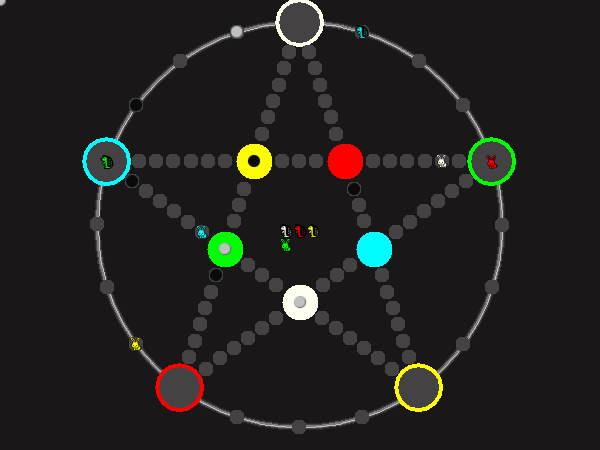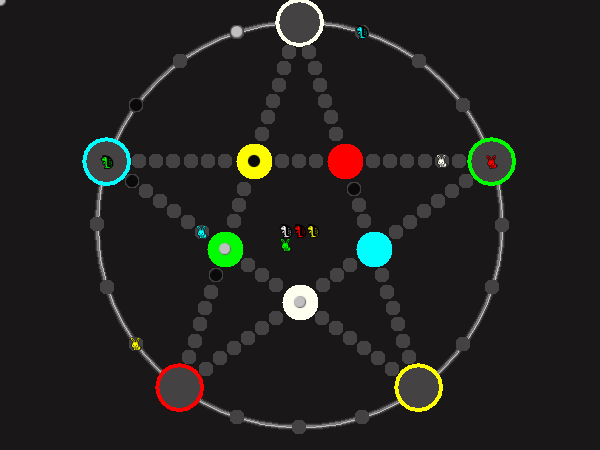
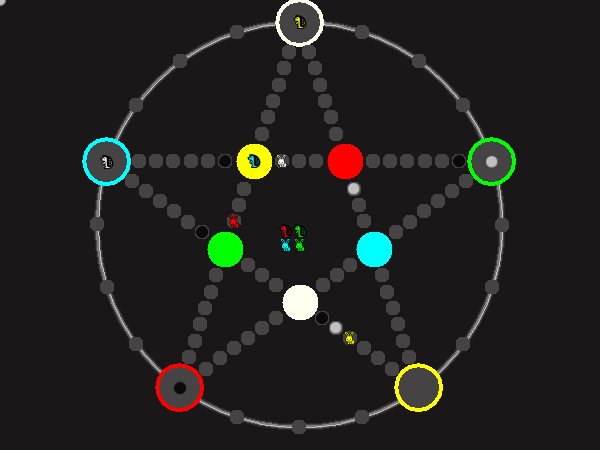
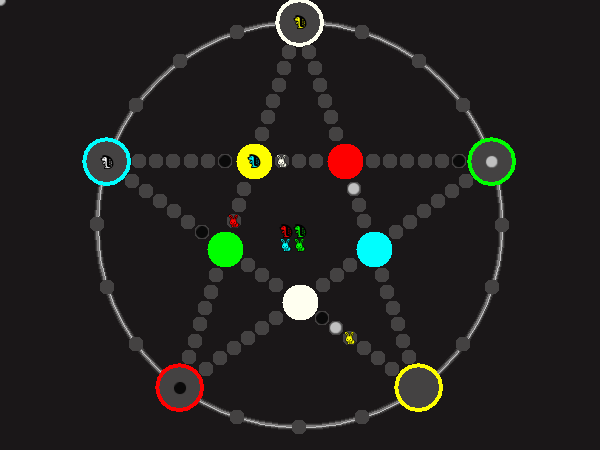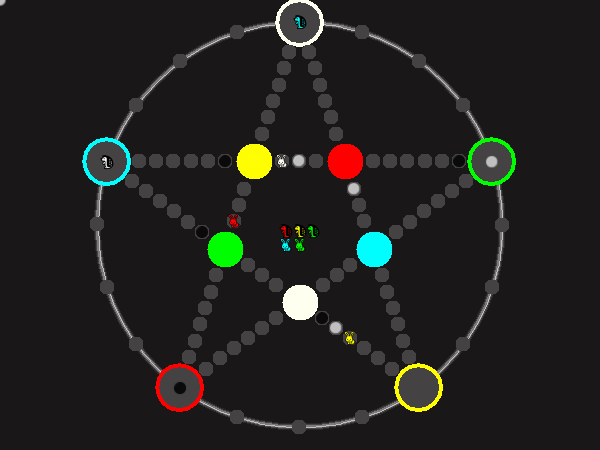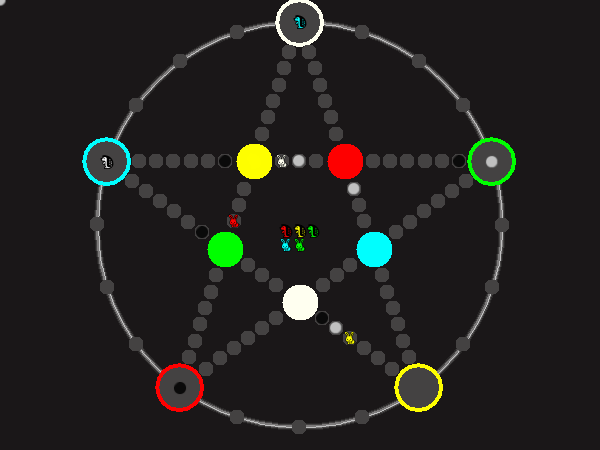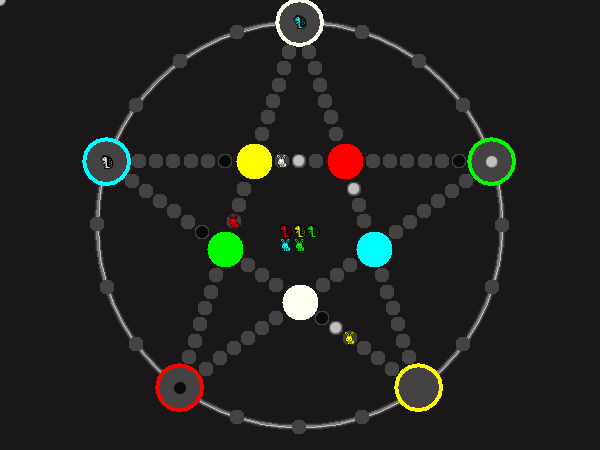
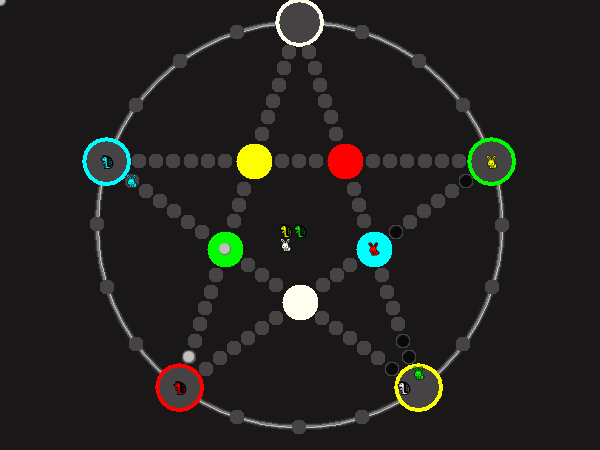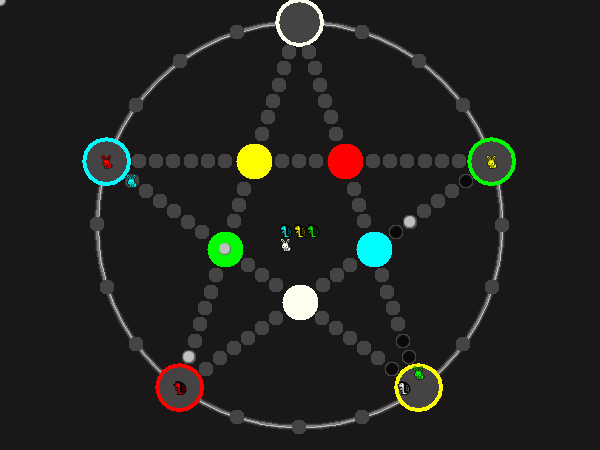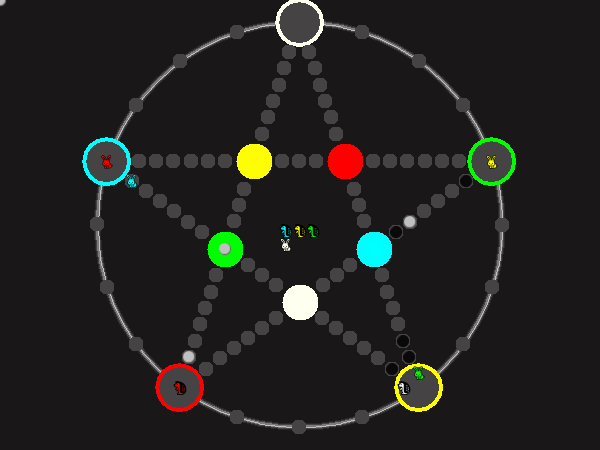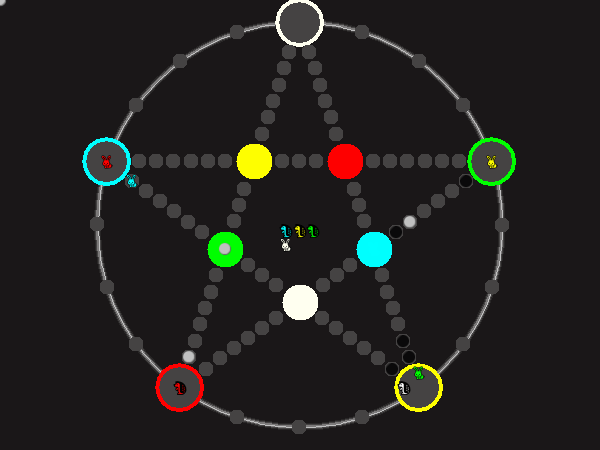
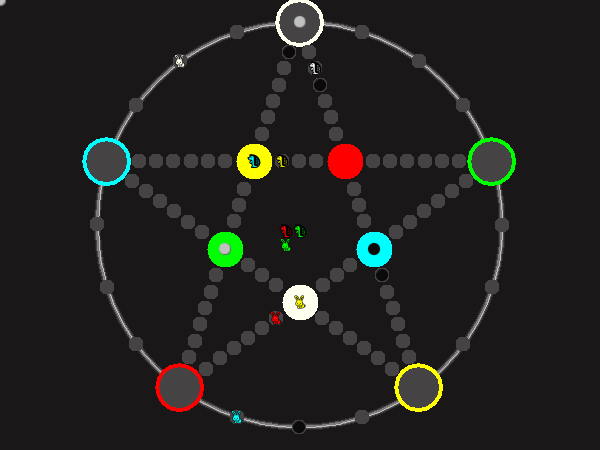
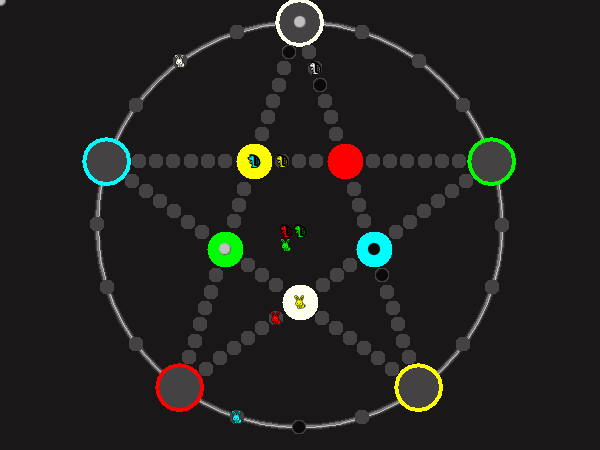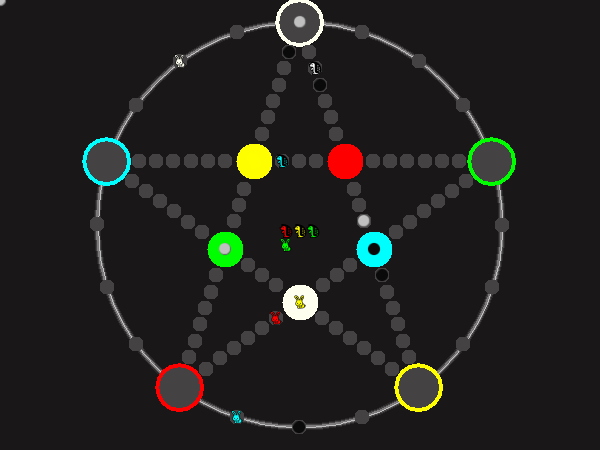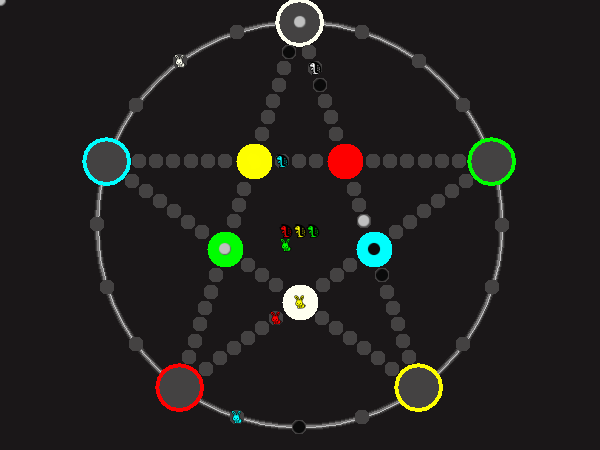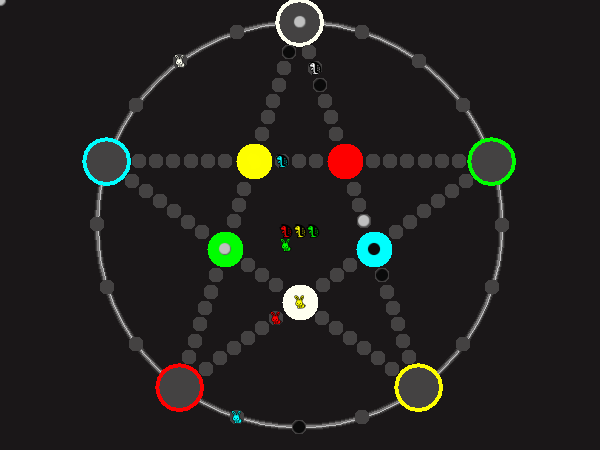
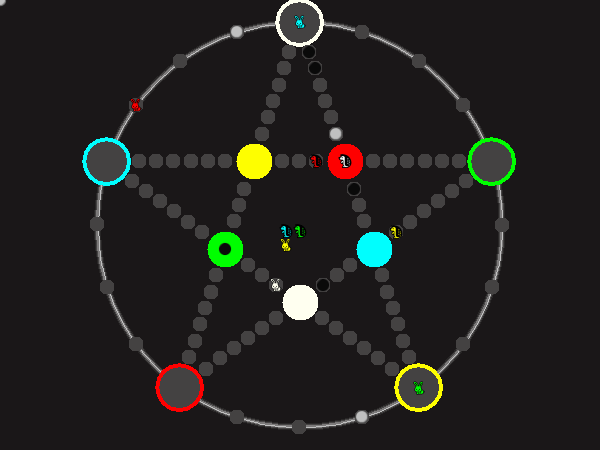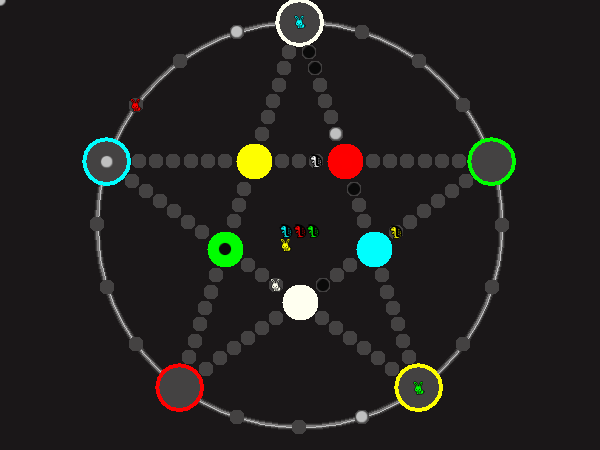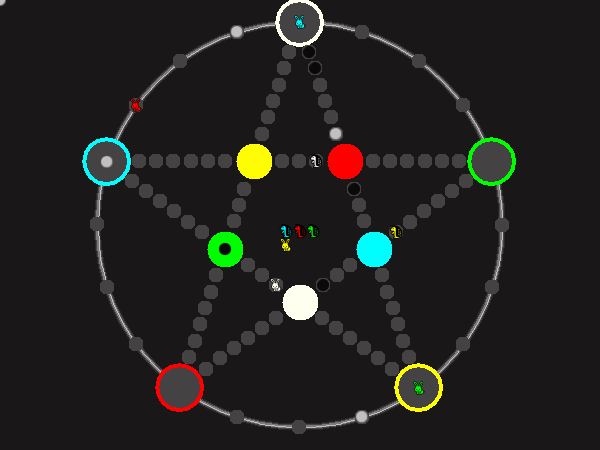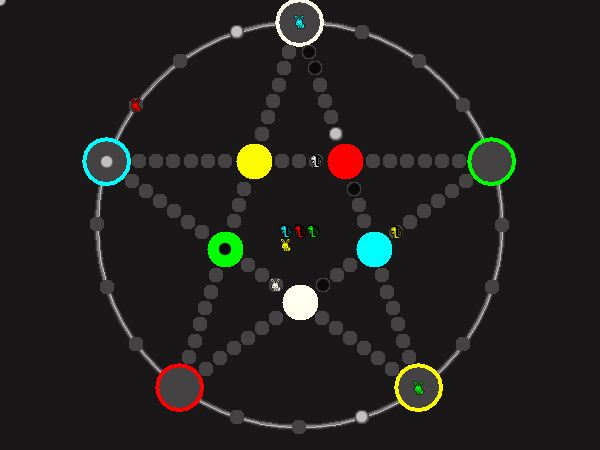
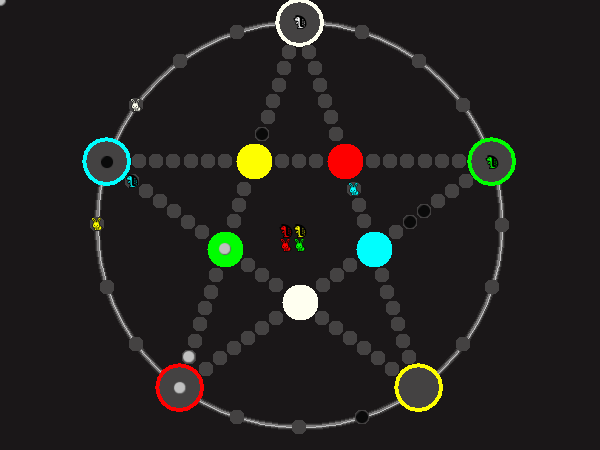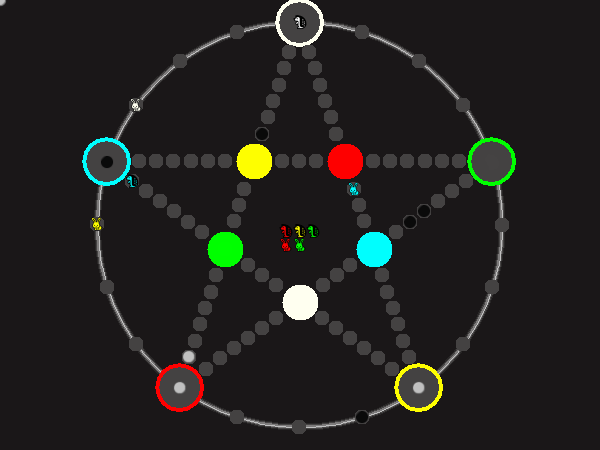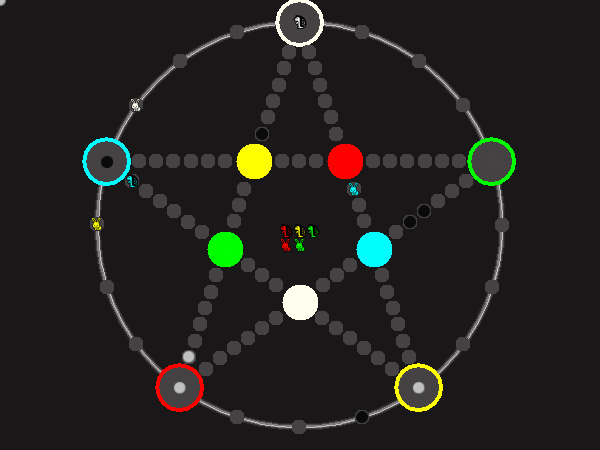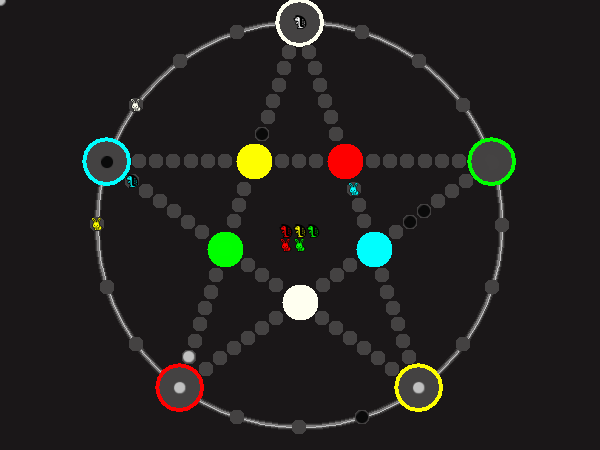
Every player plays 5 pieces of one shape, e.g. cats against pawns or whatever. Every player has one white, one blue, one red, one green and one yellow piece. All pieces start the race on the corners of their respective colors. The goal is to bring three of one's pieces from their corners to the crossing of matching color.

There are five black blocks that are neutral pieces. At the beginning they are on the crossings in the center. There are five gray blocks that come into the game as pieces reach their goals.

One can move in any direction on the star or the ring, as far as there is a free path. But one cannot jump. One can either (1) just move to an empty space, (2) beat a black block, taking its place and re-position it on another free stop somewhere, (3) swap two neighboring pieces, one of which must be one's own piece.

As Ko-rule, immediate repetition of the same move is not allowed.

A piece that reaches its destination crossing is removed from the board. A player thus moving a piece out successfully gains a gray block that she can position on any free stop. Such gray blocks are also neutral pieces, but when they get beaten, they are removed again rather than re-positioned.

Miscellaneous

General comments:

Requires αβ search to play well.

Play: Combinatorial,Multiplayer

Mechanism(s): Race

Components: Board

Level: Standard

BGG Stats

BGG Entry	Pentagame
BGG Rating	6.88364
#Voters	22
SD	3.76742
BGG Weight	3.5
#Voters	6
Year	2015

BGG Ratings and Comments

User	Rating	Comment
chuckdee68	1
KalterHund	10	Of course I give you 10 points, I love this game. Actually I don't play so many abstract games, but rather cooperative games or something like 7 Wonders, but this one... it's really amazing and I highly recommend it. There is no randomness at all, all meeples start on the same fields and then it's all about the right strategic answer to the other player's move. Although the game is relatively easy to learn, it is often not so easy to spot the best strategy. Well, I'll keep playing until I'm unbeatable. It may take a while, but luckily I was able to snag a prototype :)
JuFiN	1	oof
MungSu	1
NikkyAi	10	I am pretty much addicted to this game, also working on a digital implementation (yes the one linked in the kickstarter) I am saddened that the reception from BGG as so overwhelmingly negative
d_s_e	8
fwagler	8	Cool game, nice simple components. Especially love the 4 player/2 teams variant.
int21	9	Played prototype in 2019. Very easy to learn the rules, yet complex enough gameplay to hook you and keep you challenged for a looong time. Equally enjoyable on 2, 3 or 4 players.
Jimtbrit	N/A	Update no.9 on the Kickstarter campaign for this unreleased game suggests backers hack BGG (link below) . Shame because it might be a good game, but any creator resorting to such techniques, needs to be discouraged. https://www.kickstarter.com/projects/penta/pentagame-the-pentagram-shaped-board-game/posts/2623410
excds	10	It's a very entertaining strategy game that is kind of addictive. I've probably played at least hundred rounds and it's always fun. If you're playing one-on-one games you get a bit of understanding of the strategy of your opponent. But then you add more players and your assumptions go out the window. Specially if you're playing a multi-player game together with players you usually play one-on-one games with.
you know who	10
Spilljeger	N/A	Designer rating his own game! Never a good idea...
oneshallstand	6	First, it's a crying shame that so many have flocked to 'Perfect 10' this as it has destroyed the reputation of what isn't a terrible game. Is it a 10? No. Is it the greatest abtract game? No. but it's better than a fair few of the challngers, is easy to learn and has some interesting decisions to make. I may revise this score later but having had a couple of plays this feels like a safe bet.
pinkymadigan	1	Look at all these fake accounts giving a 10!
krachkasten	10	One of my favorite games! Edit: I decided to edit my brief judgment of the game (which still applies :D) after reading some negative posts here claiming ratings are fake, and other negative things. We are a small community in Berlin playing the game. It has been around for some years, there are prototypes and even an online version that everyone can just print. There is no commercial side to it, no one is making money of this (frankly, so far it's been quite the opposite). A kickstarter has just been started to make it more well known! The game actually got me to play board games more often (yes, I may not be a proper geek yet!), I love playing it!
Geeken	4.44
ainmosni	10	This is a great game. It's very simple to pick up, but very difficult to master. The best way I can describe how the game feels is "a stripped down version of chess that allows more than two players".
Lumenator	9
penta_jan	N/A	Though I have invented it, I really love playing it and do so every second day, no joke, for the last couple of years. And I am not the only one. Those who say this wouldn't be fair: 10 points means outstanding, want to play all the time and guess this will never change. This is the case. Please base your own rating on your own experience with this.
rsb762gm	10	Fun abstract strategy, easy to learn rules, great replayability.
Lindroth	10	One of the few abstract games that actually scales really well with more players.
cheng	1	Bogus game entry. Just Kickstarted but listed as 2012 release.
Tzer	2	enbrgtqx
Kvartsbrott	10	Played a prototype. Exceptionally easy to learn the rules, very concise. Played both with 2 and 3 players, and both were interesting enough to want to try again straight away. The game was complex enough to get you hooked and challenged. I believe its replayability is very high.
SlugFather	10	Have very much enjoyed playing this excellent game since the beginning of the century. Hoping it will achieve the popularity it deserves!

Kolomogorov Complexity Analysis

Size (bytes)	35236
Reference Size	10673
Ratio	3.30

Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.

Playout Complexity Estimate

Playouts per second	431.75 (2316.17µs/playout)
Reference Size	399010.45 (2.51µs/playout)
Ratio (low is good)	924.18

Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.

State Space Complexity

% new positions/bucket

Samples	166279
Confidence	0.00	0: totally unreliable, 100: perfect

State space complexity (where present) is an estimate of the number of distinct game tree reachable through actual play. Over a series of random games, Ai Ai checks each position to see if it is new, or a repeat of a previous position and keeps a total for each game. As the number of games increase, the quantity of new positions seen per game decreases. These games are then partitioned into a number of buckets, and if certain conditions are met, Ai Ai treats the number in each bucket as the start of a strictly decreasing geometric sequence and sums it to estimate the total state space. The accuracy is calculated as 1-[end bucket count]/[starting bucklet count]

Playout/Search Speed

Label	Its/s	SD	Nodes/s	SD	Game length	SD
Random playout	426	13	163,891	2,043	385	190
search.UCT	NaN	NaN			0	0
search.AlphaBeta	NaN	NaN			0	0

Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.

Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.

Mirroring Strategies

Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.

Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.

Heuristic Values

This chart shows the heuristic values thoughout a single representative* game. The orange line shows the difference between player scores. (* Representative, in the sense that it is close to the mean game length.)

Win % By Player (Bias)

1: Rabbit win %	44.60±3.05	Includes draws = 50%
2: Hedgehog win %	55.80±3.09	Includes draws = 50%
Tie %	0.40	Percentage of games where all players win.
Draw %	20.40	Percentage of games where all players draw.
Decisive %	79.20	Percentage of games with a single winner.
Samples	1000	Quantity of logged games played

Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)

Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.

UCT Skill Chains

Match	AI	Strong Wins	Draws	Strong Losses	#Games	Strong Score	p1 Win%	Draw%	p2 Win%	Game Length
0	Random
2	UCT (its=3)	630	2	338	970	0.6200 <= 0.6505 <= 0.6799	51.96	0.21	47.84	346.05
3	UCT (its=3)	480	8	512	1000	0.4531 <= 0.4840 <= 0.5150	49.40	0.80	49.80	291.97

Search for levels ended: time limit reached.

Level of Play: Strong beats Weak 60% of the time (lower bound with 95% confidence).

Draw%, p1 win% and game length may give some indication of trends as AI strength increases.

1st Player Win Ratios by Playing Strength

This chart shows the win(green)/draw(black)/loss(red) percentages, as UCT play strength increases. Note that for most games, the top playing strength show here will be distinctly below human standard.

Complexity

Game length	644.05
Branching factor	100.28
Complexity	10^1304.08	Based on game length and branching factor
Computational Complexity	10^6.44	Saturation reached - accuracy very high.
Samples	1000	Quantity of logged games played

Computational complexity (where present) is an estimate of the game tree reachable through actual play. For each game in turn, Ai Ai marks the positions reached in a hashtable, then counts the number of new moves added to the table. Once all moves are applied, it treats this sequence as a geometric progression and calculates the sum as n-> infinity.

Move Classification

Board Size	100	Quantity of distinct board cells
Distinct actions	82635	Quantity of distinct moves (e.g. "e4") regardless of position in game tree
Killer moves	1441	A 'killer' move is selected by the AI more than 50% of the time Too many killers to list.
Good moves	3860	A good move is selected by the AI more than the average
Bad moves	78771	A bad move is selected by the AI less than the average
Terrible moves	78325	A terrible move is never selected by the AI Too many terrible moves to list.
Response distance%	48.45%	Distance from move to response / maximum board distance; a low value suggests a game is tactical rather than strategic.
Samples	1000	Quantity of logged games played

Board Coverage

A mean of 29.49% of board locations were used per game.

Colour and size show the frequency of visits.

Game Length

Game length frequencies.

Mean	63.33
Mode	[31]
Median	30.0

Change in Material Per Turn

Mean change in material/round	0.00	Complete round of play (all players)

This chart is based on a single representative* playout, and gives a feel for the change in material over the course of a game. (* Representative in the sense that it is close to the mean length.)

Actions/turn

Table: branching factor per turn, based on a single representative* game. (* Representative in the sense that it is close to the mean game length.)

Action Types per Turn

This chart is based on a single representative* game, and gives a feel for the types of moves available throughout that game. (* Representative in the sense that it is close to the mean game length.)

Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.

Trajectory

This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).

The lead changed on 11% of the game turns. Ai Ai found 51 critical turns (turns with only one good option).

Position Heatmap

This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).

Good/Effective moves

Measure	All players	Player 1	Player 2
Mean % of effective moves	40.22	46.46	34.11
Mean no. of effective moves	44.25	58.31	30.47
Effective game space	10^624.39	10^348.15	10^276.23
Mean % of good moves	30.64	55.56	6.20
Mean no. of good moves	38.09	70.42	6.40
Good move game space	10^426.44	10^360.14	10^66.29

These figures were calculated over a single game.

An effective move is one with score 0.1 of the best move (including the best move). -1 (loss) <= score <= 1 (win)

A good move has a score > 0. Note that when there are no good moves, an multiplier of 1 is used for the game space calculation.

Quality Measures

Measure	Value	Description
Hot turns	78.96%	A hot turn is one where making a move is better than doing nothing.
Momentum	13.37%	% of turns where a player improved their score.
Correction	36.14%	% of turns where the score headed back towards equality.
Depth	4.30%	Difference in evaluation between a short and long search.
Drama	4.79%	How much the winner was behind before their final victory.
Foulup Factor	97.03%	Moves that looked better than the best move after a short search.
Surprising turns	5.94%	Turns that looked bad after a short search, but good after a long one.
Last lead change	95.30%	Distance through game when the lead changed for the last time.
Decisiveness	1.24%	Distance from the result being known to the end of the game.

These figures were calculated over a single representative* game, and based on the measures of quality described in "Automatic Generation and Evaluation of Recombination Games" (Cameron Browne, 2007). (* Representative, in the sense that it is close to the mean game length.)

Openings

Moves	Animation
W Rabbit@0-22xBlack,Black-31,W Hedgehog@0-31xBlack,Black-3,W Rabbit@22-21xBlack,Black-22,W Hedgehog@31-23xBlack,Black-87,W Rabbit@21-87xBlack,Black-36
W Rabbit@0-22xBlack,Black-31,W Hedgehog@0-31xBlack,Black-3,W Rabbit@22-21xBlack,Black-22,W Hedgehog@31-23xBlack,Black-87,W Rabbit@21-87xBlack,Black-94
W Rabbit@0-22xBlack,Black-34,W Hedgehog@0-34xBlack,Black-3,W Rabbit@22-21xBlack,Black-22,W Hedgehog@34-23xBlack,Black-87,W Rabbit@21-87xBlack,Black-36
W Rabbit@0-22xBlack,Black-34,W Hedgehog@0-34xBlack,Black-3,W Rabbit@22-21xBlack,Black-22,W Hedgehog@34-23xBlack,Black-87,W Rabbit@21-87xBlack,Black-94
W Rabbit@0-23xBlack,Black-25,W Hedgehog@0-25xBlack,Black-17,W Rabbit@23-24xBlack,Black-23,W Hedgehog@25-22xBlack,Black-97,W Rabbit@24-97xBlack,Black-90
W Rabbit@0-22xBlack,Black-31,W Hedgehog@0-31xBlack,Black-3,W Rabbit@22-21xBlack,Black-22,W Hedgehog@31-23xBlack,Black-87,W Rabbit@21-87xBlack
W Rabbit@0-22xBlack,Black-34,W Hedgehog@0-34xBlack,Black-3,W Rabbit@22-21xBlack,Black-22,W Hedgehog@34-23xBlack,Black-87,W Rabbit@21-87xBlack
W Rabbit@0-23xBlack,Black-25,W Hedgehog@0-25xBlack,Black-17,W Rabbit@23-24xBlack,Black-23,W Hedgehog@25-22xBlack,Black-97,W Rabbit@24-97xBlack
W Rabbit@0-23xBlack,Black-25,W Hedgehog@0-25xBlack,Black-17,W Rabbit@23-24xBlack,Black-23,W Hedgehog@25-22xBlack,Black-97
W Rabbit@0-22xBlack,Black-31,W Hedgehog@0-31xBlack,Black-3,W Rabbit@22-21xBlack,Black-22,W Hedgehog@31-23xBlack,Black-87
W Rabbit@0-22xBlack,Black-34,W Hedgehog@0-34xBlack,Black-3,W Rabbit@22-21xBlack,Black-22,W Hedgehog@34-23xBlack,Black-87
W Rabbit@0-23xBlack,Black-25,W Hedgehog@0-25xBlack,Black-17,W Rabbit@23-24xBlack,Black-23,W Hedgehog@25-22xBlack

Puzzle	Solution
Hedgehog to win in 5 moves
Hedgehog to win in 3 moves
Hedgehog to win in 3 moves
Rabbit to win in 4 moves
Rabbit to win in 4 moves
Rabbit to win in 4 moves
Hedgehog to win in 2 moves
Hedgehog to win in 2 moves
Hedgehog to win in 2 moves
Hedgehog to win in 2 moves
Hedgehog to win in 2 moves
Hedgehog to win in 2 moves