Last to move wins.
Generated at 12/02/2022, 16:36 from 1000 logged games.
Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!
Be the last to move.
Each turn, pick up a stack with your colour on top, then proceed to sow it around the board. You may change direction after each drop, but may not backtrack.
General comments:
Play: Combinatorial
Mechanism(s): Stalemate,Territory,Movement
| BGG Entry | Pilare |
|---|---|
| BGG Rating | 7.375 |
| #Voters | 24 |
| SD | 1.31696 |
| BGG Weight | 3.8 |
| #Voters | 5 |
| Year | 2005 |
| User | Rating | Comment |
|---|---|---|
| WasQ | 7 | |
| unic | 6.5 | |
| garea37 | 6 | |
| miceu | 9 | |
| mrraow | 9 | A clever stacking game on a small board. Despite a large branching factor caused by the sowing mechanism, there's scope for strategic play as well as tactics. |
| zaphiel | 8.5 | |
| capsmolet | N/A | 6x6 |
| grasa_total | 7 | I'd like to play more-- the wrinkle that you sometimes want to 'capture' your own pieces in order to double-capture later is a new one to me. I was a little worried this would end up like my elementary-school dodgeball games: unending, because all of a piece's captures can be 'undone' by an enemy capturing the stack and then re-sowing them. No one ever really dies! But that's a mirage. The thing to look at is not whether my pieces can take yours out of the game forever, it's that at the start of the game the neutral pieces are all on the bottoms of stacks, and adding them to the mix is what gradually powers down the game. |
| dooz | 7 | |
| Pensator | 7 | 2 player game I plays in homemade sets |
| mafko | 8.5 | |
| pulla | 5 | Too chaotic for my tastes. Possibly also not enough depth to keep going for long. |
| solisatrus | 9 | Elegant rules that allow some surprisingly deep play. It's a remarkable game in that the tipping point is not immediately apparent (at least to me) lol. Very fun. *Great* job Jorge! Muy bien! |
| Zickzack | 7 | I am a sucker for games with simple rules and complex results. In this case, the game mechanism is even simpler to show than to write down. And it shows that there is an overlap between stacking and Mancala games. The "neutral" pieces - which are more the enemy of both sides - are an important part of the game though. Gameplay tends to be short - 15 to 20 moves. And early attacks spell disaster. It is important to create stacks in one's own area of influence first. Experience must tell, if there is more strategy to it or if the rest is sheer tactics. |
| rayzg | 5 | The game starts off really fun as the board options shrink dramatically. Then players are forces to release their opponent's pieces and the game starts to drag. |
| dave doma | 10 | |
| demongod | N/A | Made |
| Schachtelhalm | 7 | An abstract stacking game with neutral pieces. Unlike Dvonn, the positions of the pieces in the stack are important. Maybe the stack height should be limited. Otherwise a fine game. |
| schwarzspecht | 8 | |
| vbroca | 6 | |
| hojoh | N/A | http://www.iggamecenter.com/info/nl/pilare.html |
| Jugular | 8 | So early on in my experience with it I'm enjoying the immensely. I'm not entirely sure how much strategy there is to be had and it appears to veer slightly more on the tyactical side but it's a great game and some strategic/tactical tips are making themselves known to me. Very very good sowing/stacking game. |
| bluebee2 | N/A | PnP |
| dbucak | 8 | Pilare involves moving stacks of pieces by distributing them, similar to Domination, Dvonn, Abande or Tak. The objective is to immobilize your opponent, which is a simpler objective than any of those games. I prefer the connection goals of Tak, but this is a fun game too. |
| arcticnights | N/A | Thrive 6x6 board + Padante poker chips. 10 blue 10 red 36 white neutral |
| STICKPIN | 7.5 | We've only played a few times ... 8x8. It seems to be a very good game, and we hope to play it many more times. Easily made with pieces at hand. Again, a good game. Rating could go up with further play. |
| glanfam | 6 | |
| FiveStars | 9 | This is an extremely interesting game. Very subtle tactics, exciting endgame. Try it on a larger board (8x8) and you get a brain-burner. |
| pezpimp | 6 | Based on one play: I like the idea and the game play was good up until the end. You "sow" your pieces around the board, just dropping a token on each space you pass in a goal to control all the stacks (meaning your color is on top). But getting them all is difficult and the game goes back and forth, overstaying its welcome a little. Even so, still a pretty good game. |
| Size (bytes) | 27672 |
|---|---|
| Reference Size | 10673 |
| Ratio | 2.59 |
Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.
| Playouts per second | 447.36 (2235.33µs/playout) |
|---|---|
| Reference Size | 2137208.81 (0.47µs/playout) |
| Ratio (low is good) | 4777.36 |
Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.
Not enough data for an accurate prediction, or game does not support hashing
State space complexity (where present) is an estimate of the number of distinct game tree reachable through actual play. Over a series of random games, Ai Ai checks each position to see if it is new, or a repeat of a previous position and keeps a total for each game. As the number of games increase, the quantity of new positions seen per game decreases. These games are then partitioned into a number of buckets, and if certain conditions are met, Ai Ai treats the number in each bucket as the start of a strictly decreasing geometric sequence and sums it to estimate the total state space. The accuracy is calculated as 1-[end bucket count]/[starting bucklet count]
| Label | Its/s | SD | Nodes/s | SD | Game length | SD |
|---|---|---|---|---|---|---|
| Random playout | 14,069 | 257 | 13,904,437 | 254,747 | 988 | 79 |
| search.UCT | 448 | 64 | 854 | 265 | ||
| search.AlphaBeta | 425,566 | 76,350 | 259 | 116 |
Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.
Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.
Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.
Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.
This chart shows the heuristic values thoughout a single representative* game. The orange line shows the difference between player scores. (* Representative, in the sense that it is close to the mean game length.)
| 1: Red win % | 52.00±3.10 | Includes draws = 50% |
|---|---|---|
| 2: White win % | 48.00±3.08 | Includes draws = 50% |
| Draw % | 0.00 | Percentage of games where all players draw. |
| Decisive % | 100.00 | Percentage of games with a single winner. |
| Samples | 1000 | Quantity of logged games played |
Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)
Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.
| Match | AI | Strong Wins | Draws | Strong Losses | #Games | Strong Score | p1 Win% | Draw% | p2 Win% | Game Length |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Random | |||||||||
| 1 | UCT (its=2) | 47 | 0 | 19 | 66 | 0.5936 <= 0.7121 <= 0.8073 | 54.55 | 0.00 | 45.45 | 25939.14 |
| 2 | UCT (its=2) | 477 | 0 | 523 | 1000 | 0.4462 <= 0.4770 <= 0.5080 | 49.10 | 0.00 | 50.90 | 16836.73 |
Search for levels ended: time limit reached.
Level of Play: Strong beats Weak 60% of the time (lower bound with 95% confidence).
Draw%, p1 win% and game length may give some indication of trends as AI strength increases.
This chart shows the win(green)/draw(black)/loss(red) percentages, as UCT play strength increases. Note that for most games, the top playing strength show here will be distinctly below human standard.
| Game length | 247.60 | |
|---|---|---|
| Branching factor | 3.83 | |
| Complexity | 10^131.48 | Based on game length and branching factor |
| Samples | 1000 | Quantity of logged games played |
Computational complexity (where present) is an estimate of the game tree reachable through actual play. For each game in turn, Ai Ai marks the positions reached in a hashtable, then counts the number of new moves added to the table. Once all moves are applied, it treats this sequence as a geometric progression and calculates the sum as n-> infinity.
| Board Size | 36 | Quantity of distinct board cells |
|---|---|---|
| Distinct actions | 73 | Quantity of distinct moves (e.g. "e4") regardless of position in game tree |
| Good moves | 40 | A good move is selected by the AI more than the average |
| Bad moves | 32 | A bad move is selected by the AI less than the average |
| Response distance% | 10.00% | Distance from move to response / maximum board distance; a low value suggests a game is tactical rather than strategic. |
| Samples | 1000 | Quantity of logged games played |
A mean of 98.49% of board locations were used per game.
Colour and size show the frequency of visits.
Game length frequencies.
| Mean | 247.60 |
|---|---|
| Mode | [164, 183, 226, 236, 244] |
| Median | 224.5 |
Table: branching factor per turn, based on a single representative* game. (* Representative in the sense that it is close to the mean game length.)
This chart is based on a single representative* game, and gives a feel for the types of moves available throughout that game. (* Representative in the sense that it is close to the mean game length.)
Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.
This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).
The lead changed on 5% of the game turns. Ai Ai found 37 critical turns (turns with only one good option).
This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).
| Measure | All players | Player 1 | Player 2 |
|---|---|---|---|
| Mean % of effective moves | 76.49 | 78.63 | 74.20 |
| Mean no. of effective moves | 2.72 | 2.83 | 2.60 |
| Effective game space | 10^92.10 | 10^51.29 | 10^40.81 |
| Mean % of good moves | 45.85 | 59.02 | 31.80 |
| Mean no. of good moves | 1.65 | 2.04 | 1.23 |
| Good move game space | 10^54.66 | 10^36.63 | 10^18.03 |
These figures were calculated over a single game.
An effective move is one with score 0.1 of the best move (including the best move). -1 (loss) <= score <= 1 (win)
A good move has a score > 0. Note that when there are no good moves, an multiplier of 1 is used for the game space calculation.
| Measure | Value | Description |
|---|---|---|
| Hot turns | 72.18% | A hot turn is one where making a move is better than doing nothing. |
| Momentum | 24.60% | % of turns where a player improved their score. |
| Correction | 41.94% | % of turns where the score headed back towards equality. |
| Depth | 2.85% | Difference in evaluation between a short and long search. |
| Drama | 3.51% | How much the winner was behind before their final victory. |
| Foulup Factor | 46.37% | Moves that looked better than the best move after a short search. |
| Surprising turns | 6.85% | Turns that looked bad after a short search, but good after a long one. |
| Last lead change | 58.47% | Distance through game when the lead changed for the last time. |
| Decisiveness | 6.45% | Distance from the result being known to the end of the game. |
These figures were calculated over a single representative* game, and based on the measures of quality described in "Automatic Generation and Evaluation of Recombination Games" (Cameron Browne, 2007). (* Representative, in the sense that it is close to the mean game length.)
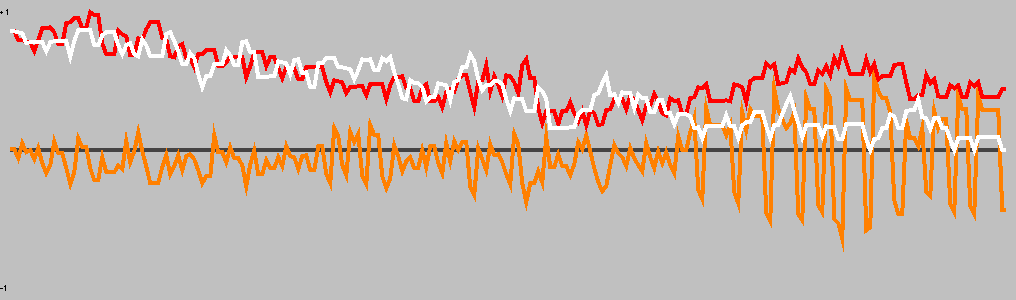
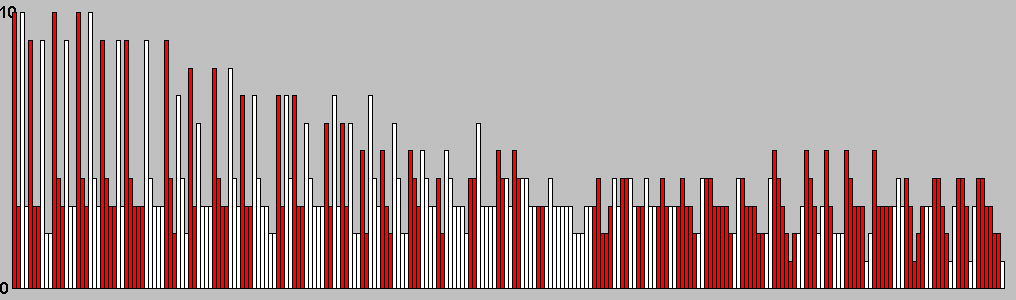
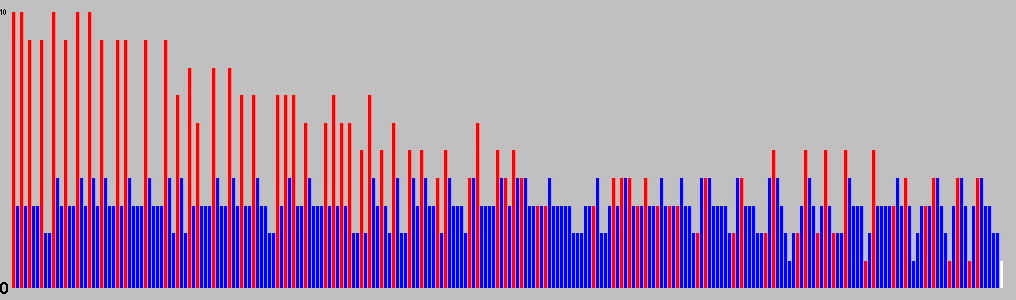
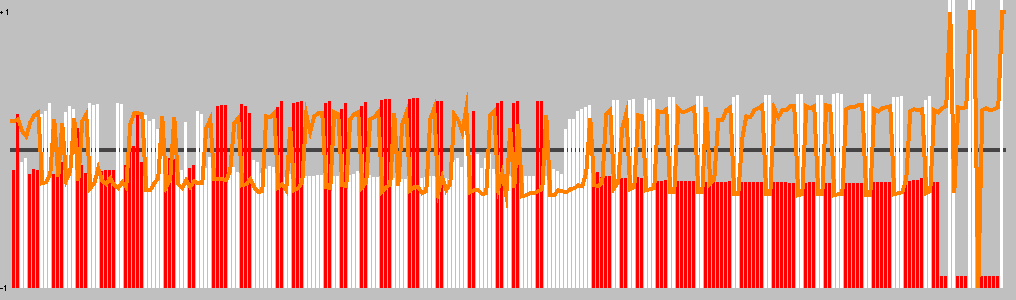
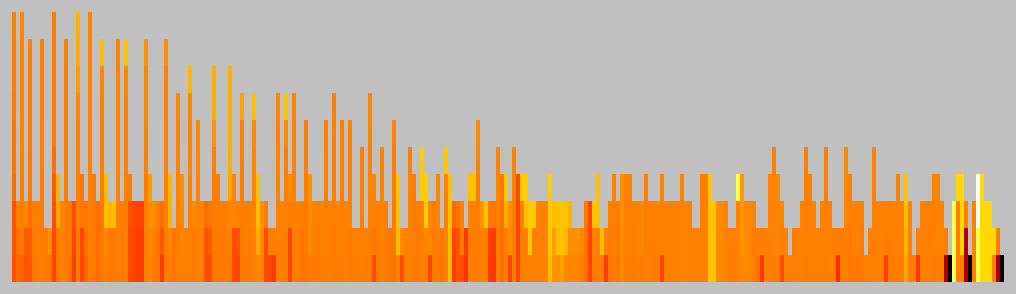
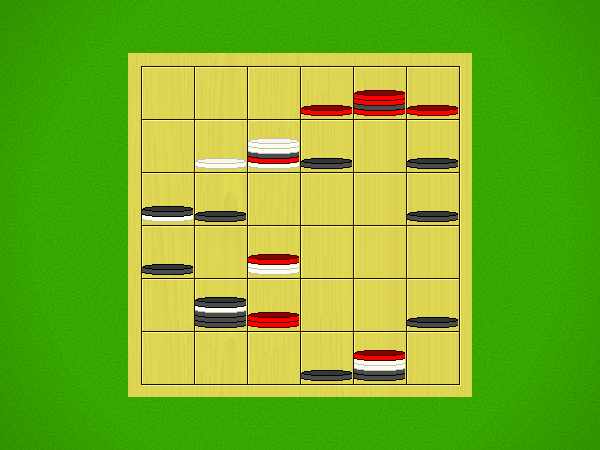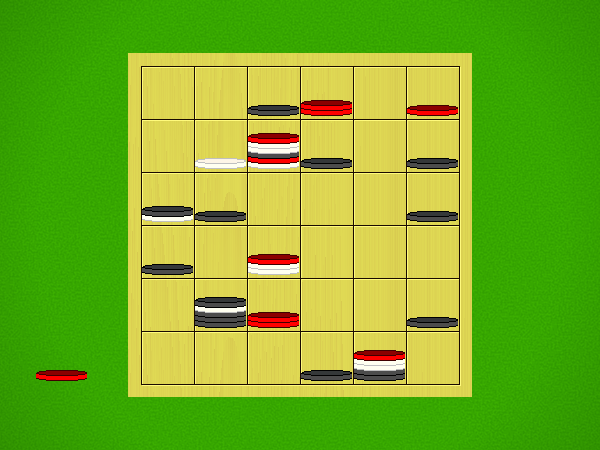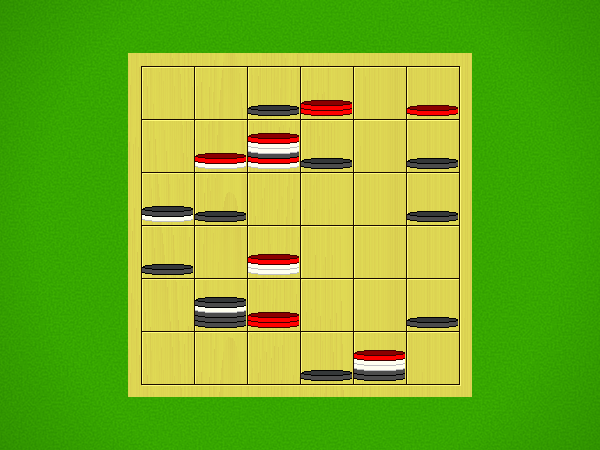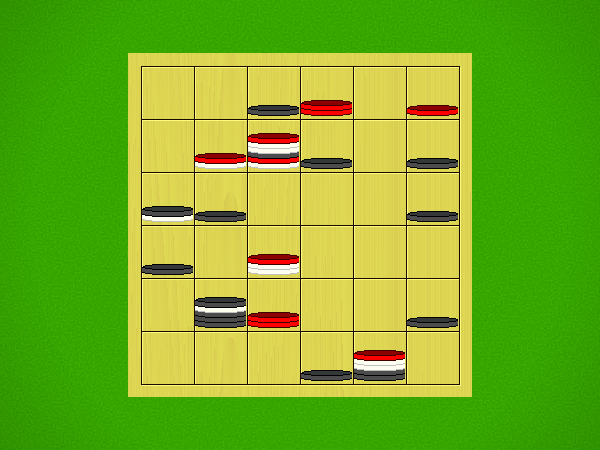
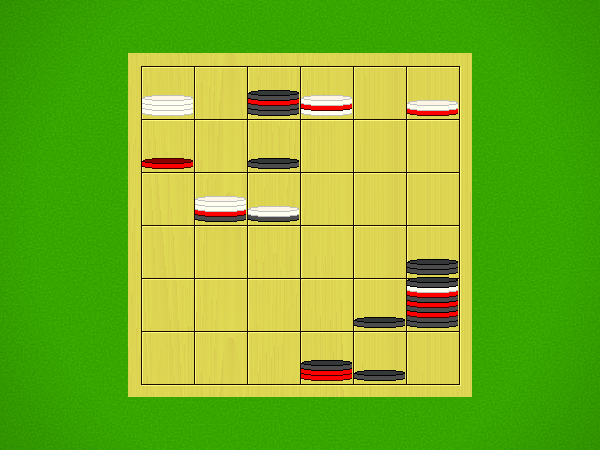
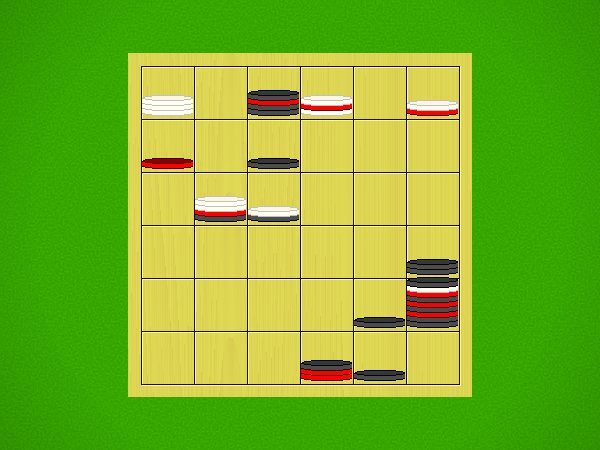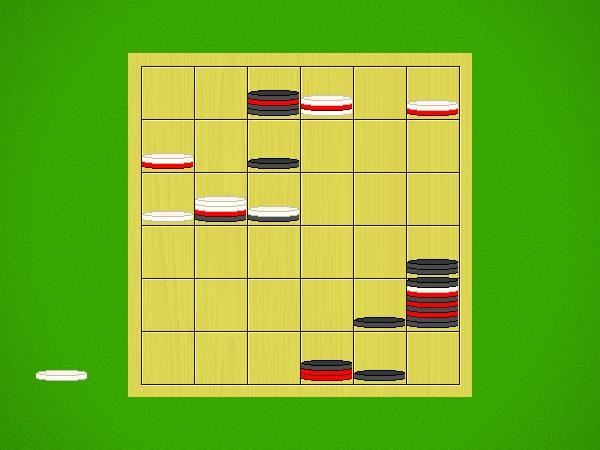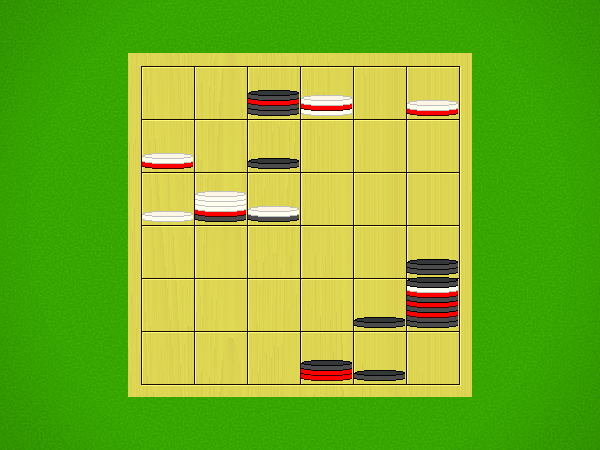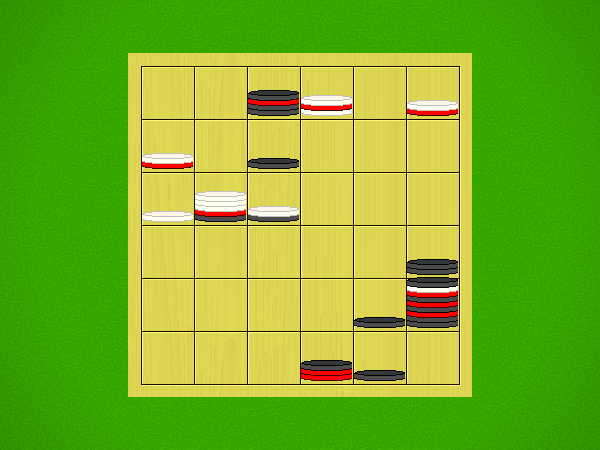
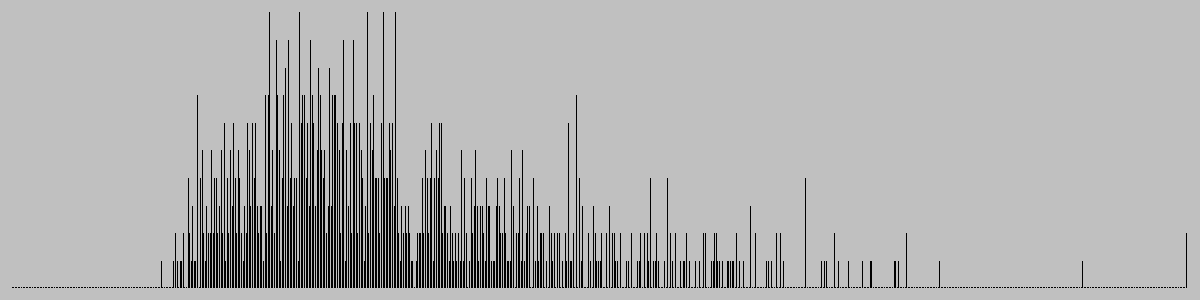| Moves | Animation |
|---|---|
| Pick Up a1,Sow a2,Pick Up a4,Sow b4,Pick Up a3,Sow a2,Pick Up b4,Sow b5,Sow c5,Pick Up a2 |  |
| Pick Up a1,Sow a2,Pick Up d6,Sow c6,Pick Up a2,Sow a3,Sow a4,Pick Up c6,Sow c5,Sow b5 |  |
| Pick Up a1,Sow b1,Pick Up a4,Sow a5,Pick Up b1,Sow b2,Sow c2,Pick Up a6,Sow a5,Pick Up a2 |  |
| Pick Up c1,Sow d1,Pick Up a5,Sow a4,Pick Up a3,Sow a4,Pick Up a6,Sow a5,Pick Up a2,Sow a3 |  |
| Pick Up c1,Sow b1,Pick Up f4,Sow f3,Pick Up f2,Sow f3,Pick Up f6,Sow f5,Pick Up e1,Sow f1 |  |
| Pick Up c1,Sow b1,Pick Up a6,Sow b6,Pick Up b1,Sow b2,Sow b3,Pick Up b6,Sow b5,Sow c5 |  |
| Pick Up c1,Sow b1,Pick Up c6,Sow d6,Pick Up b1,Sow b2,Sow b3,Pick Up d6,Sow d5,Sow e5 |  |
| Pick Up e1,Sow d1,Pick Up f4,Sow f3,Pick Up f2,Sow f3,Pick Up f6,Sow f5,Pick Up f3,Sow e3 |  |
| Pick Up e1,Sow d1,Pick Up a6,Sow b6,Pick Up d1,Sow d2,Sow d3,Pick Up b6,Sow b5,Sow b4 |  |
| Pick Up f1,Sow f2,Pick Up a4,Sow a5,Pick Up f2,Sow f3,Sow f4,Pick Up a5,Sow a4,Sow a3 |  |
| Pick Up a2,Sow a3,Pick Up e6,Sow f6,Pick Up a3,Sow a4,Sow b4,Pick Up a5,Sow a4,Pick Up b4 |  |
| Pick Up a2,Sow a3,Pick Up f6,Sow f5,Pick Up a3,Sow a4,Sow a5,Pick Up a6,Sow a5,Pick Up f3 |  |
Colour shows the success ratio of this play over the first 10moves; black < red < yellow < white.
Size shows the frequency this move is played.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 38 | 316 | 1094 | 8318 | 20276 | 108397 | 289980 | 1261241 | 3543525 | 11292207 | 33797056 |
Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.
No solutions found to depth 12.
| Puzzle | Solution |
|---|---|
 Red to win in 6 moves | |
 White to win in 5 moves |
Weak puzzle selection criteria are in place; the first move may not be unique.
