Change in Material Per Turn
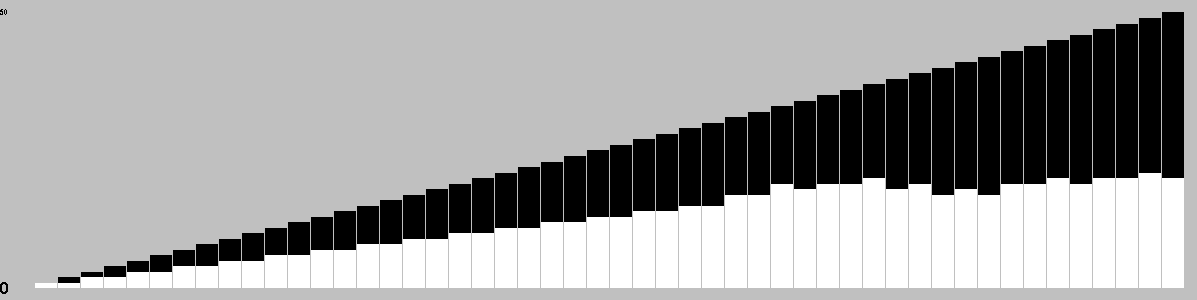
This chart is based on a single playout, and gives a feel for the change in material over the course of a game.
An orthogonal connection game.
On each turn, a player must place a single own-stone on any empty point. If as a direct result of the placement, a player has two own-stones that are orthogonally adjacent to an enemy stone at a right angle, then that enemy stone is converted to an own-stone.
If the newly converted stone creates conditions for a similar capture, then that capture takes place immediately, and so on in a chain reaction. A capturing pair (i.e. the two own-stones that bring about a capture of an enemy stone) must contain at least one newly placed or newly converted stone, otherwise no capture takes place.
A player's goal is to connect his/her two same-coloured board sides with a group of orthogonally-connected stones of his/her colour.
In the variant of Pinch in which captured stones are removed (rather than flipped to the opposite colour), on the next turn, a player cannot play a stone into the cell just vacated by a captured stone.
General comments:
Play: Combinatorial
Family: Combinatorial 2019
Mechanism(s): Connection
Components: Board
| BGG Entry | Pinch |
|---|---|
| BGG Rating | 0 |
| #Voters | 0 |
| SD | 0 |
| BGG Weight | 0 |
| #Voters | 0 |
| Year | 2019 |
| AI | Strong Wins | Draws | Strong Losses | #Games | Strong Win% | p1 Win% | Game Length |
|---|---|---|---|---|---|---|---|
| Random | |||||||
| Grand Unified UCT(U1-T,rSel=s, secs=0.01) | 36 | 0 | 0 | 36 | 100.00 | 44.44 | 104.72 |
| Grand Unified UCT(U1-T,rSel=s, secs=0.03) | 36 | 0 | 2 | 38 | 94.74 | 50.00 | 93.61 |
| Grand Unified UCT(U1-T,rSel=s, secs=0.07) | 36 | 0 | 11 | 47 | 76.60 | 57.45 | 81.13 |
| Grand Unified UCT(U1-T,rSel=s, secs=0.20) | 36 | 0 | 4 | 40 | 90.00 | 45.00 | 67.55 |
| Grand Unified UCT(U1-T,rSel=s, secs=0.55) | 36 | 0 | 9 | 45 | 80.00 | 37.78 | 61.71 |
Level of Play: Strong beats Weak 60% of the time (lower bound with 90% confidence).
Draw%, p1 win% and game length may give some indication of trends as AI strength increases; but be aware that the AI can introduce bias due to horizon effects, poor heuristics, etc.
| Size (bytes) | 27256 |
|---|---|
| Reference Size | 10293 |
| Ratio | 2.65 |
Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.
| Playouts per second | 17301.34 (57.80µs/playout) |
|---|---|
| Reference Size | 363081.84 (2.75µs/playout) |
| Ratio (low is good) | 20.99 |
Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.
| 1: Player 1 (Black) win % | 48.70±3.09 | Includes draws = 50% |
|---|---|---|
| 2: Player 2 (White) win % | 51.30±3.10 | Includes draws = 50% |
| Draw % | 0.00 | Percentage of games where all players draw. |
| Decisive % | 100.00 | Percentage of games with a single winner. |
| Samples | 1000 | Quantity of logged games played |
Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)
Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.
| Label | Its/s | SD | Nodes/s | SD | Game length | SD |
|---|---|---|---|---|---|---|
| Random playout | 23,645 | 159 | 3,409,189 | 22,885 | 144 | 14 |
| search.UCB | 27,223 | 6,281 | 58 | 27 | ||
| search.UCT | 47,314 | 3,769 | 1 | 3 |
Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.
Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.
Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.
Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.
| Game length | 84.29 | |
|---|---|---|
| Branching factor | 127.37 | |
| Complexity | 10^176.07 | Based on game length and branching factor |
| Computational Complexity | 10^7.35 | Sample quality (100 best): 33.04 |
| Samples | 1000 | Quantity of logged games played |
| Distinct actions | 170 | Number of distinct moves (e.g. "e4") regardless of position in game tree |
|---|---|---|
| Good moves | 83 | A good move is selected by the AI more than the average |
| Bad moves | 87 | A bad move is selected by the AI less than the average |
| Samples | 1000 | Quantity of logged games played |

This chart is based on a single playout, and gives a feel for the change in material over the course of a game.
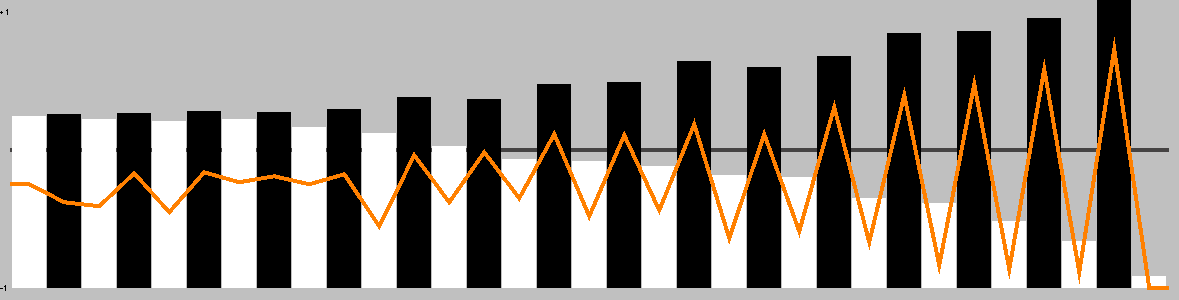
This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).
The lead changed on 33% of the game turns. Ai Ai found 0 critical turns (turns with only one good option).
Overall, this playout was 54.55% hot.

This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).

Table: branching factor per turn.
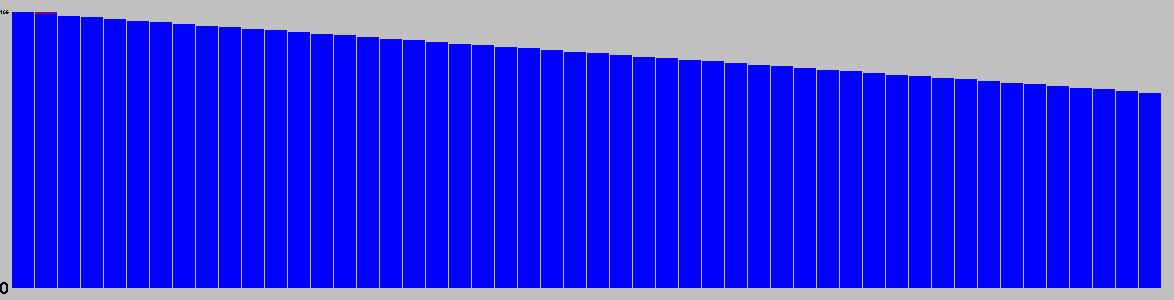
This chart is based on a single playout, and gives a feel for the types of moves available over the course of a game.
Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.
| 0 | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 169 | 28730 | 2427854 |
Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.
No solutions found to depth 3.
| Moves | Animation |
|---|---|
| k6,m5 |  |
| g11,g4 |  |
| g12,i1 |  |
| m13,k3 |  |
| k1,m7 |  |
| g3,d5 |  |
| d4,g10 |  |
| l4,m2 |  |
| m4,f3 |  |
| h5,k2 |  |
| a7,b7 |  |
| b7,m9 |  |
| m9,h10 |  |
| c11,b9 |  |
| b12,j11 |  |
| l12,e8 |  |
| a1,j6 |  |
| b1,i4 |  |
| h1,k4 |  |
| e3,j1 |  |