Rules

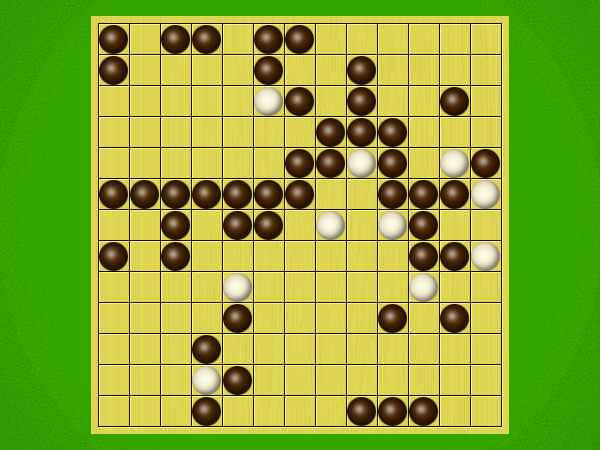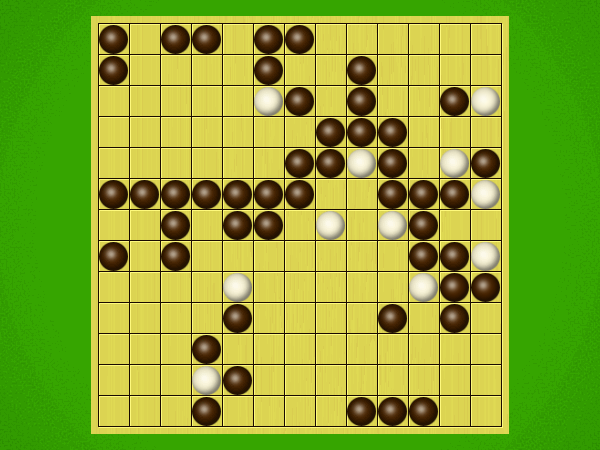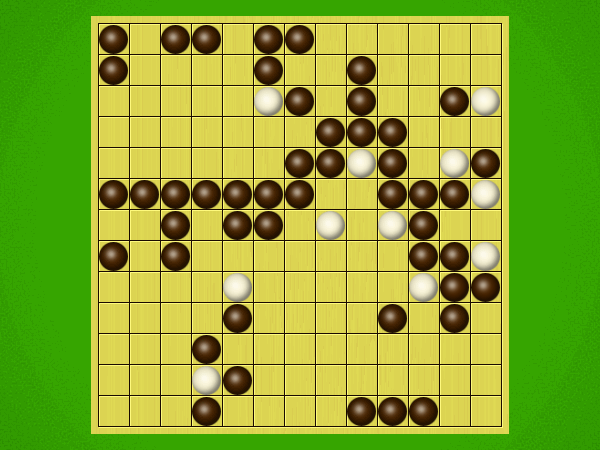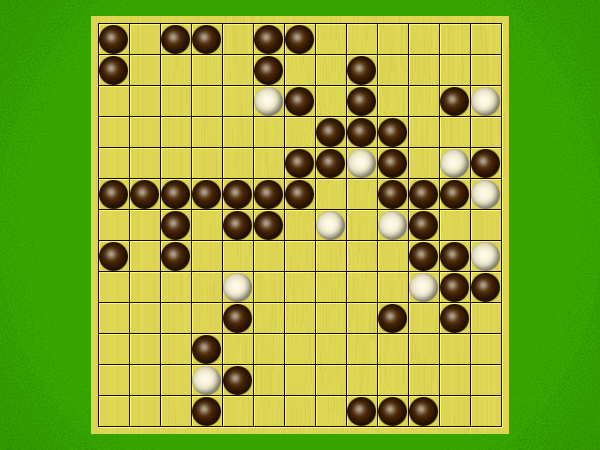
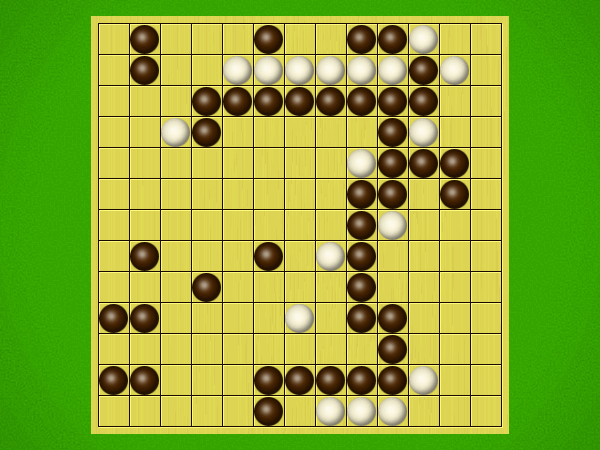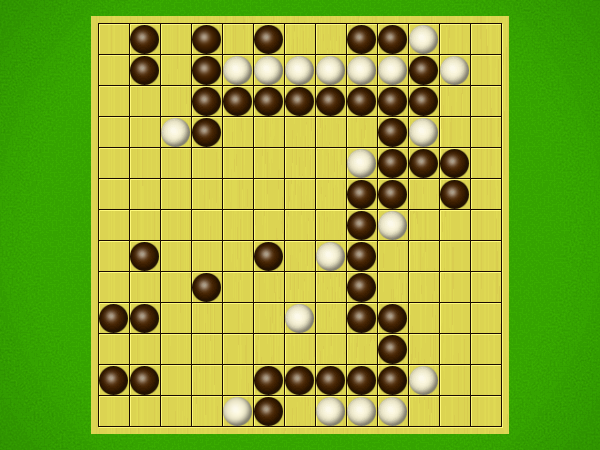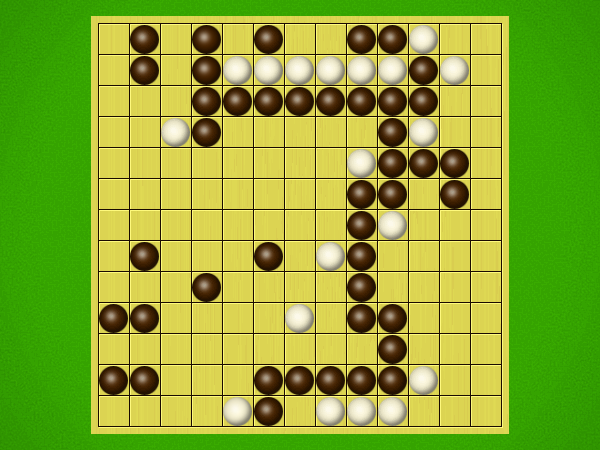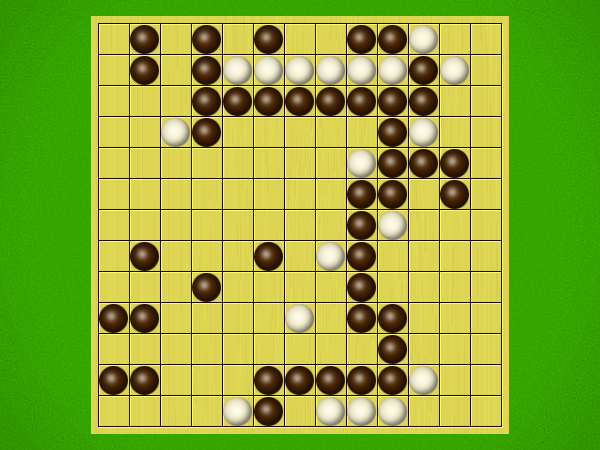
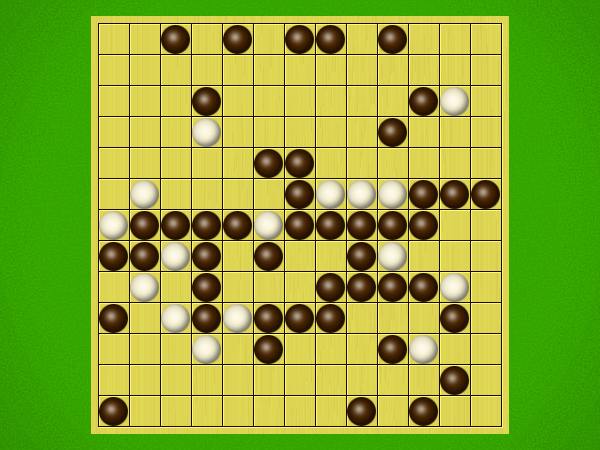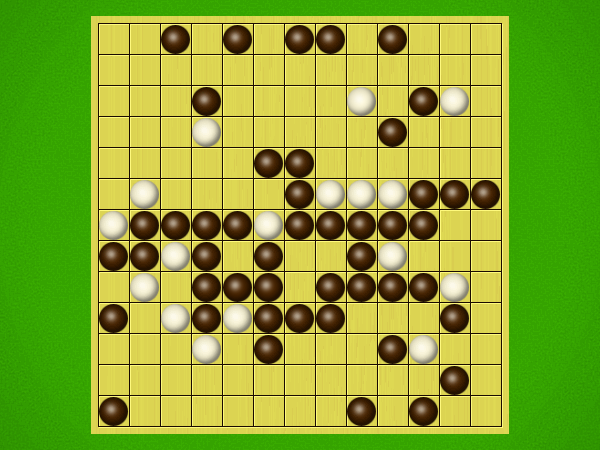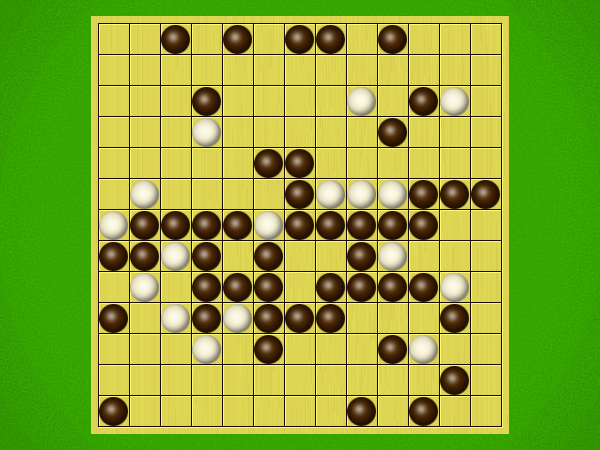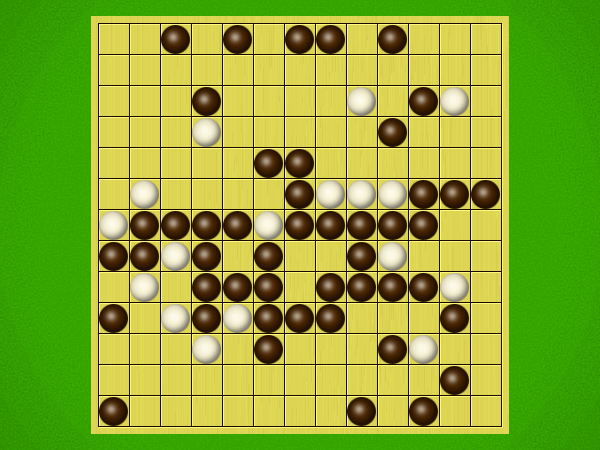
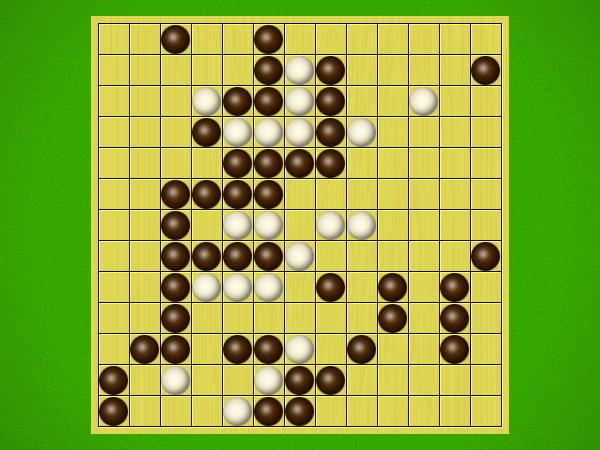
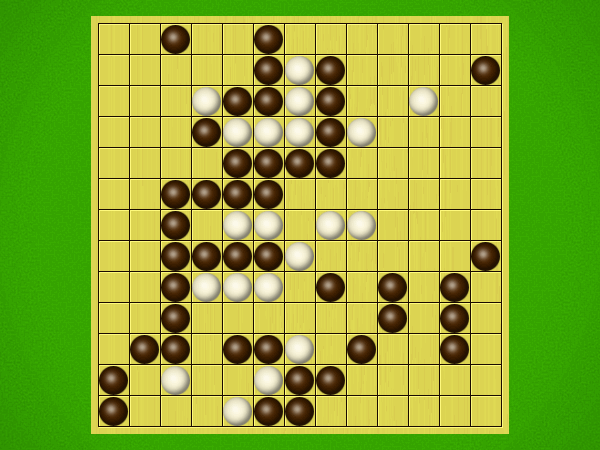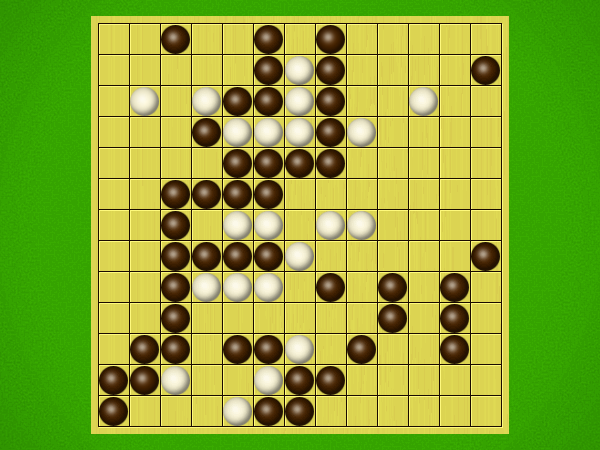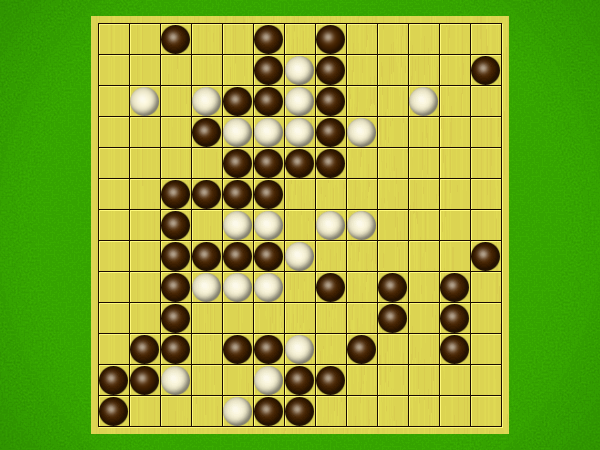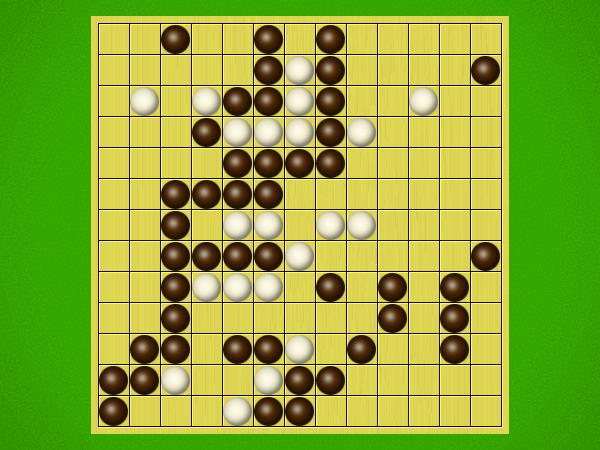
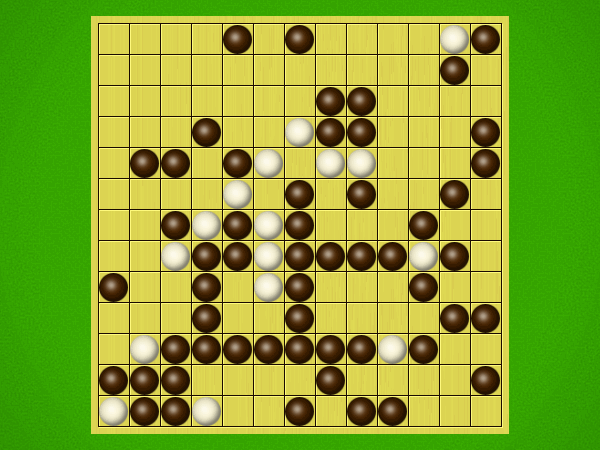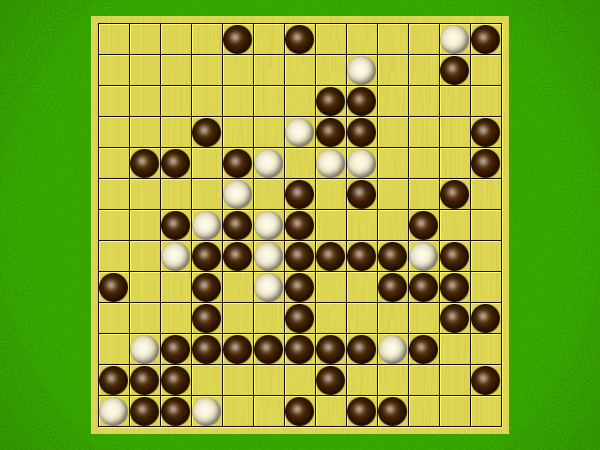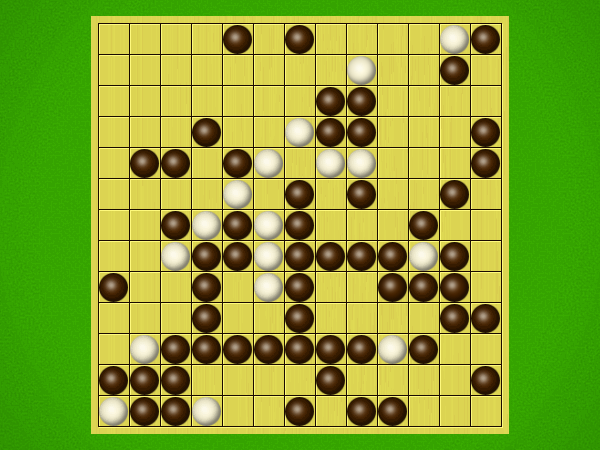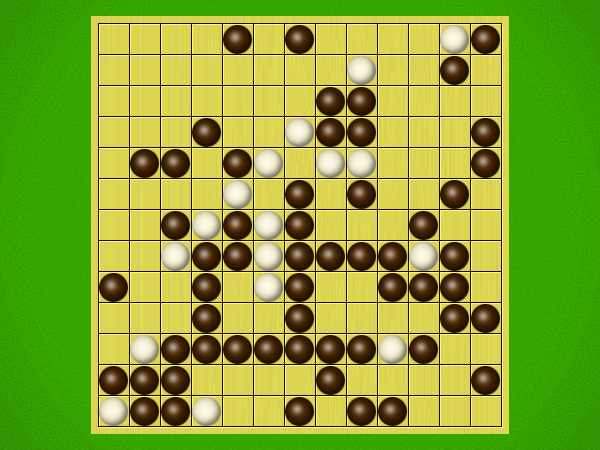
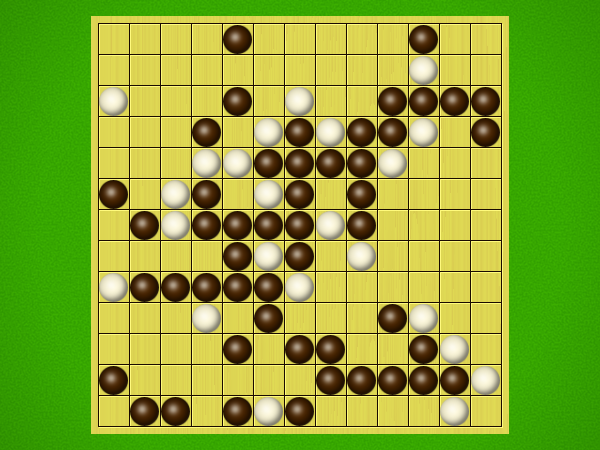
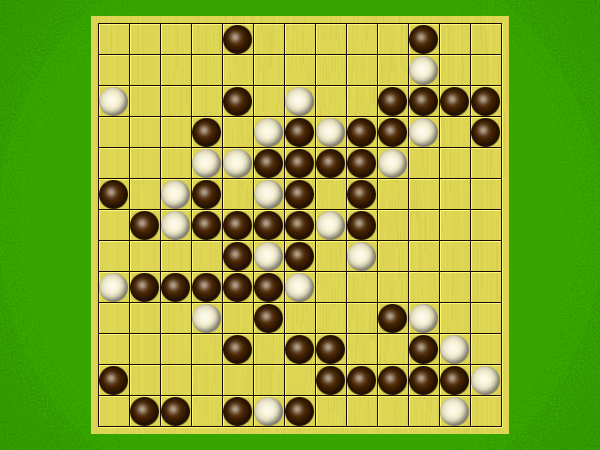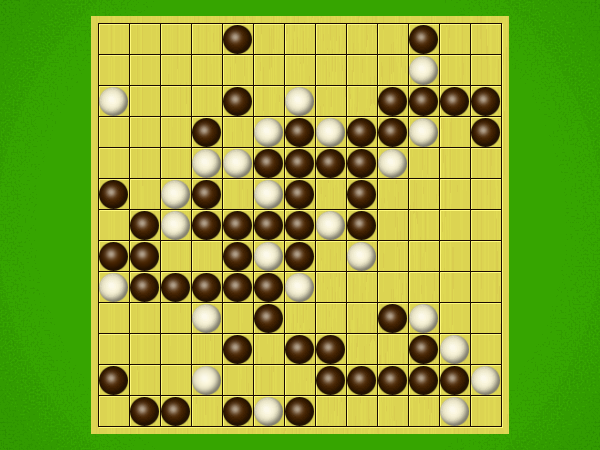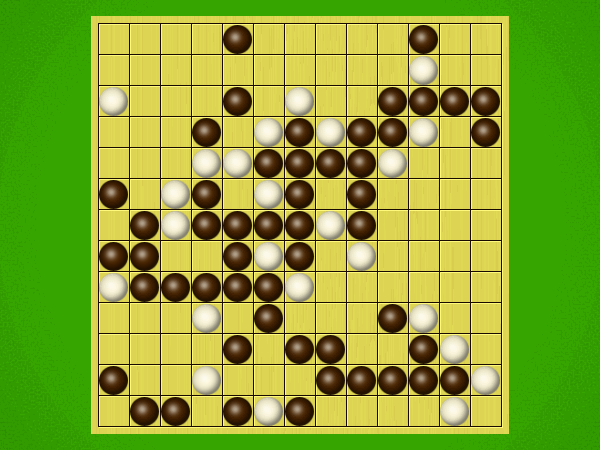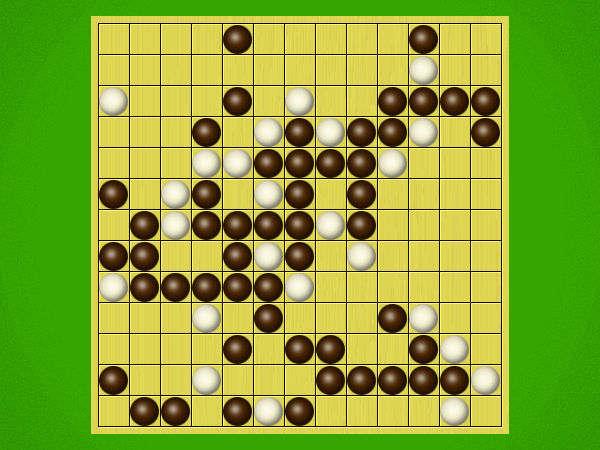
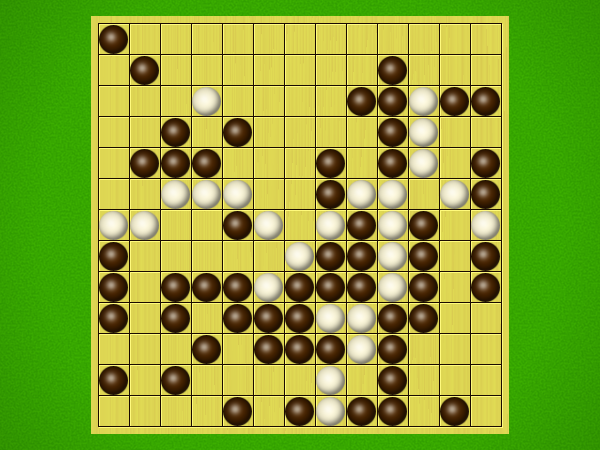
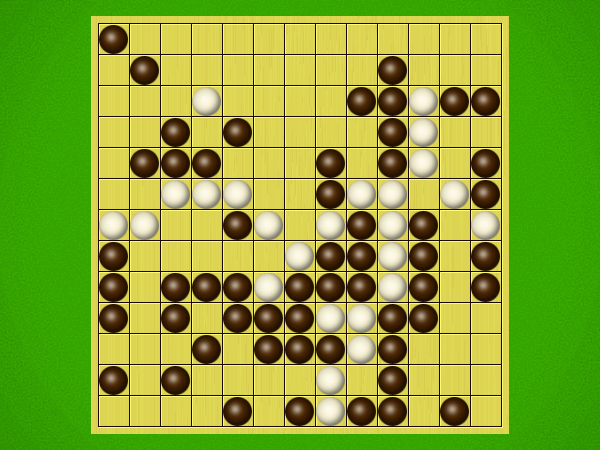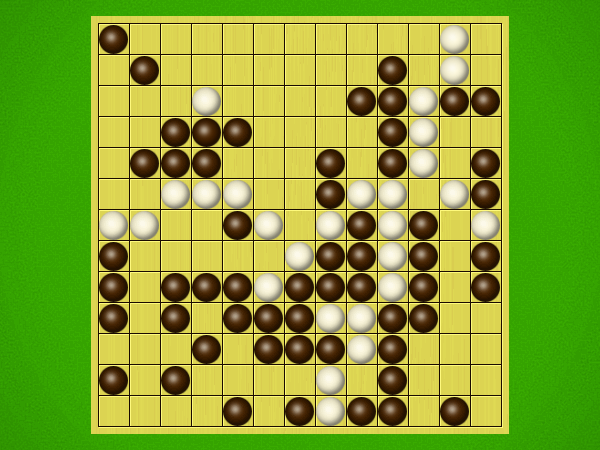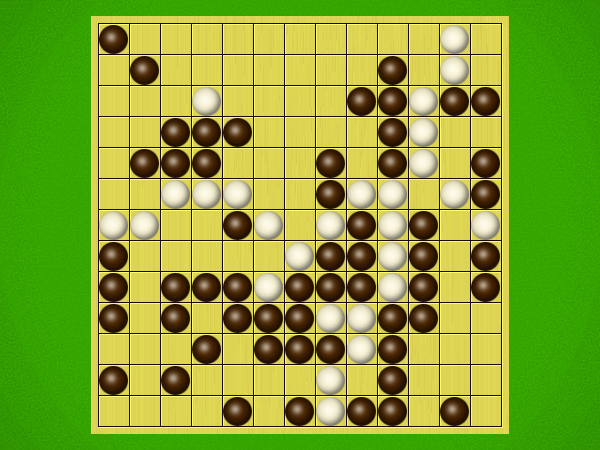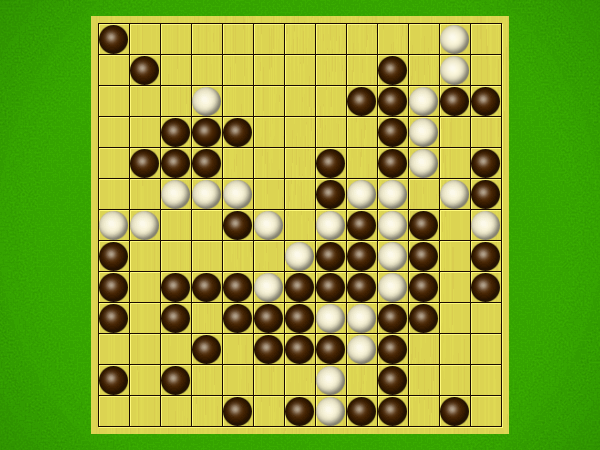
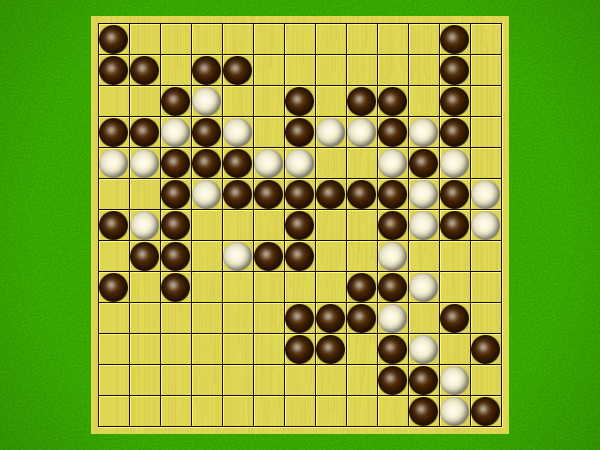
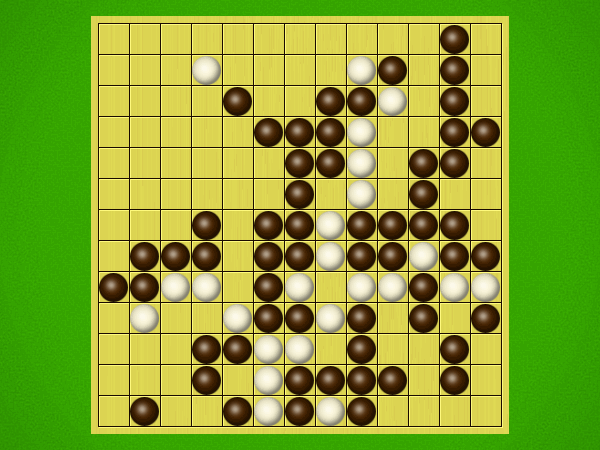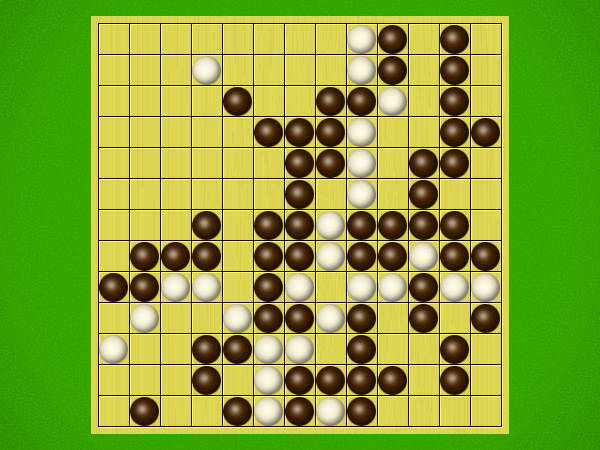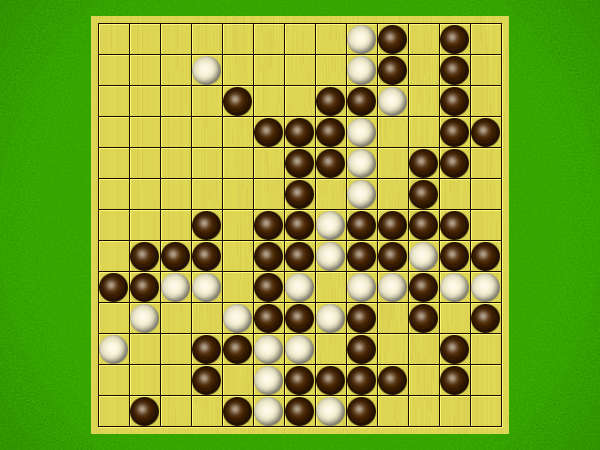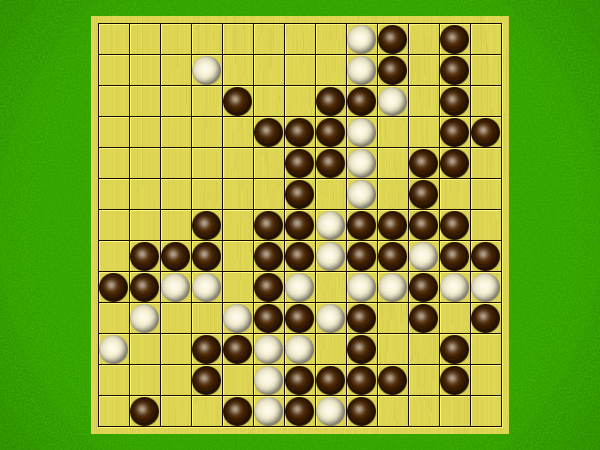
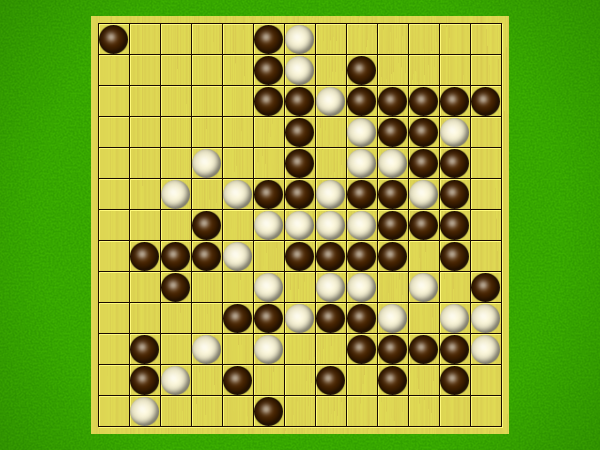
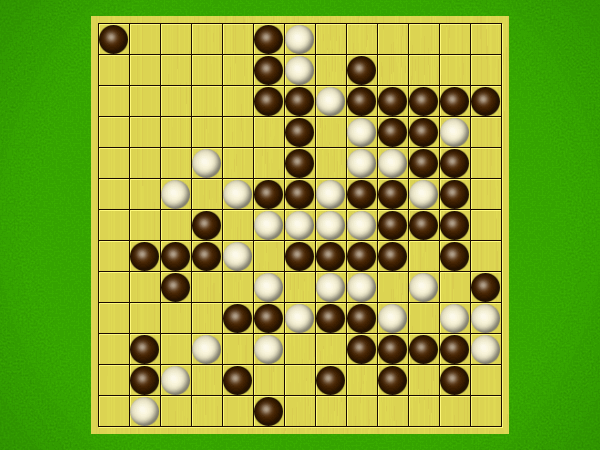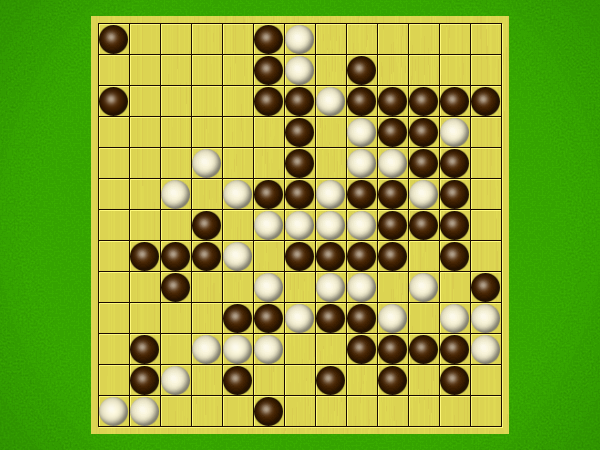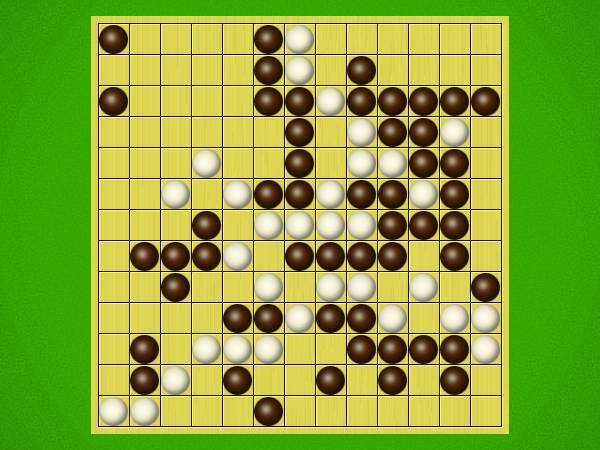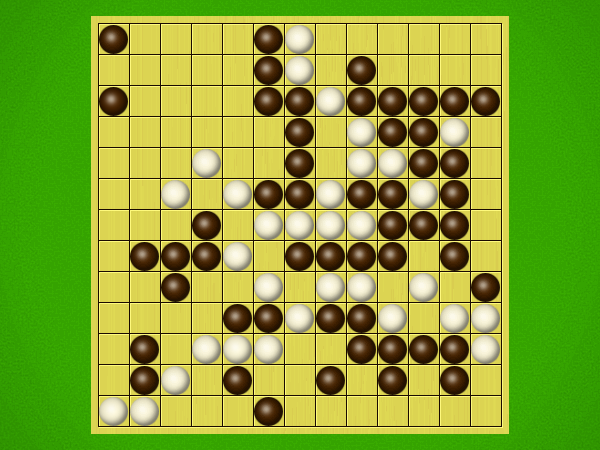
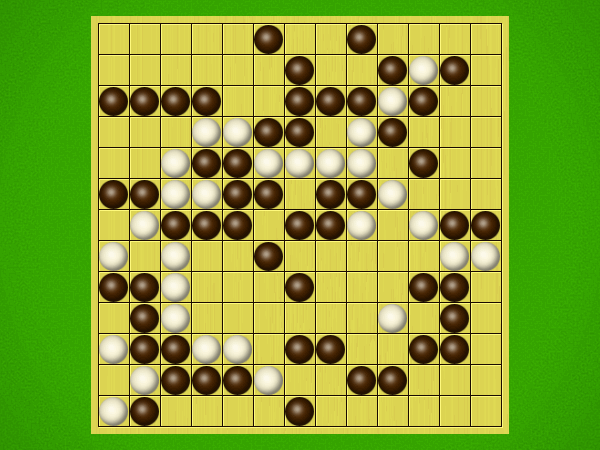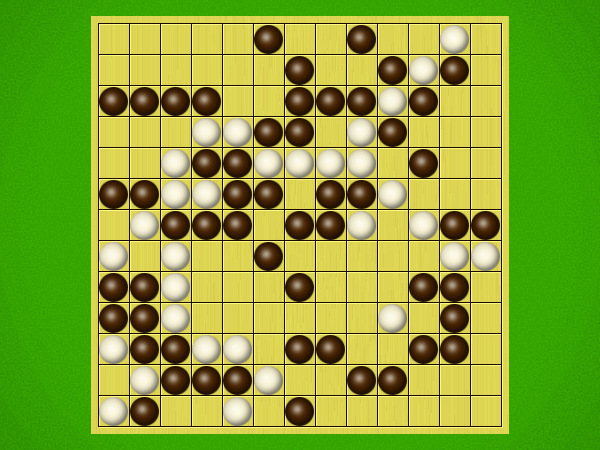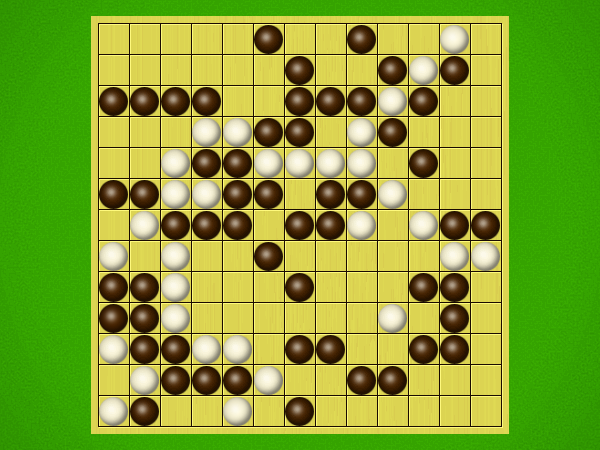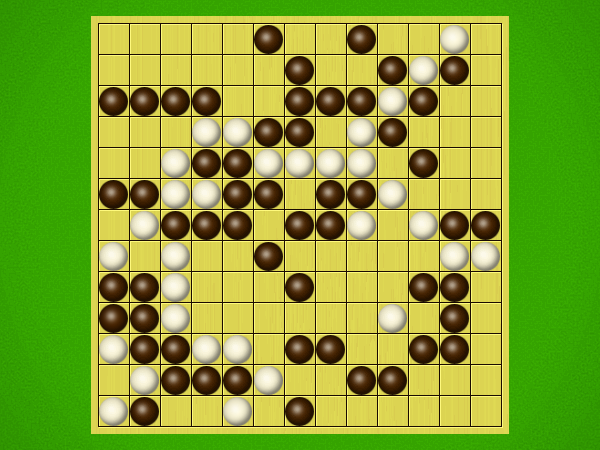
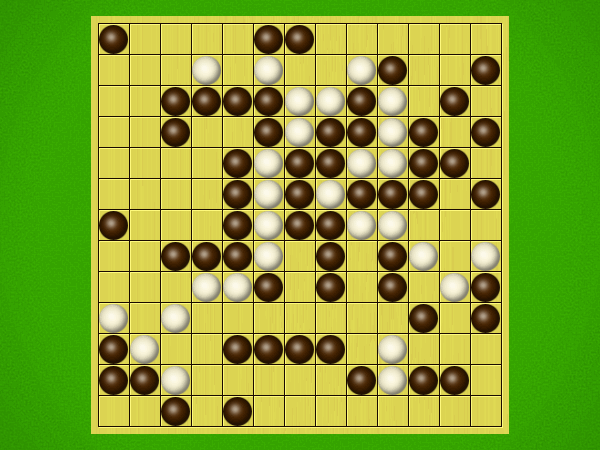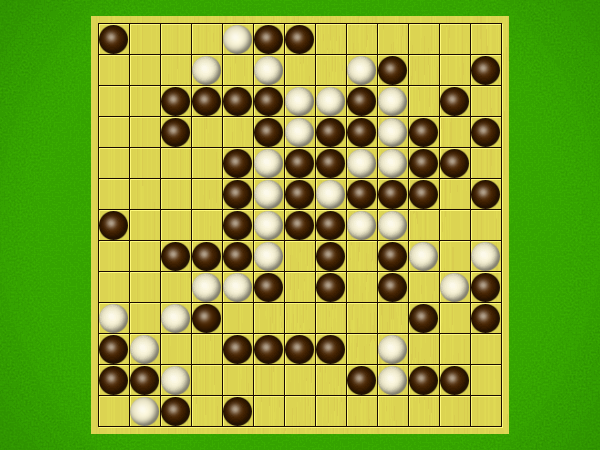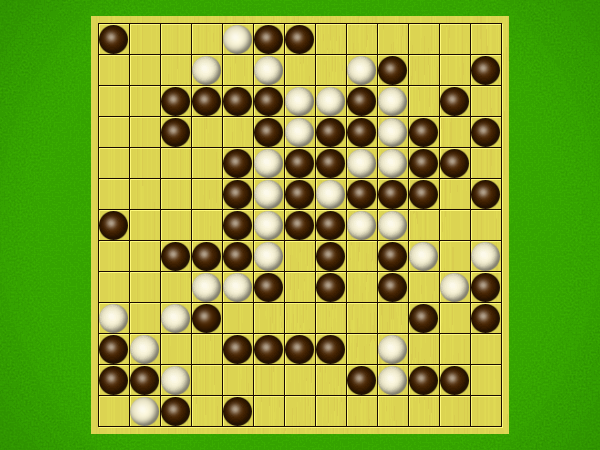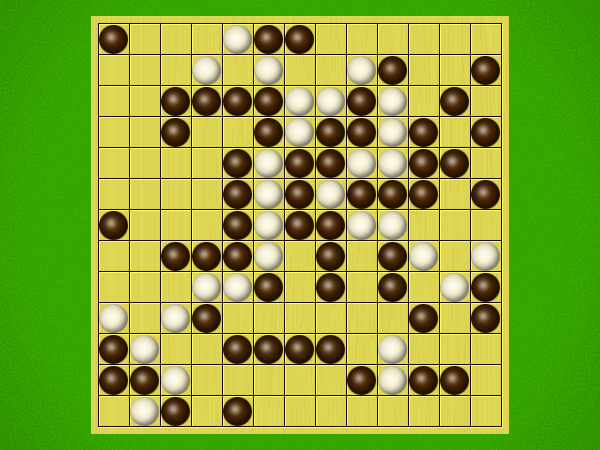
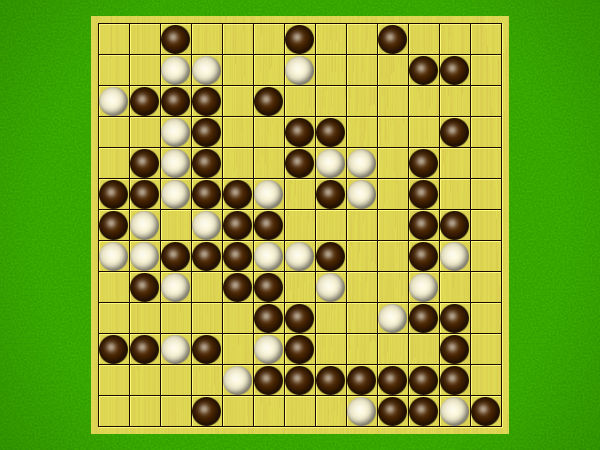
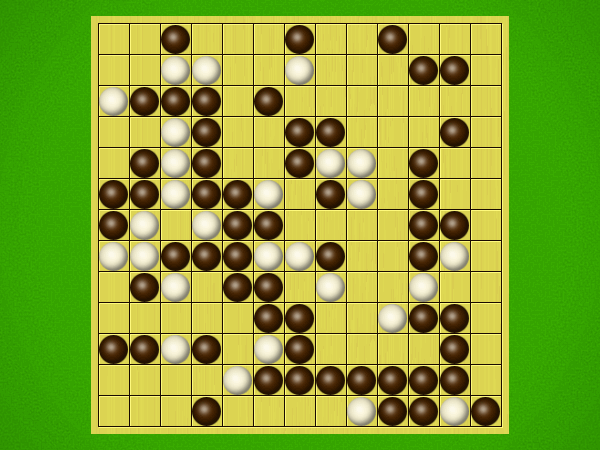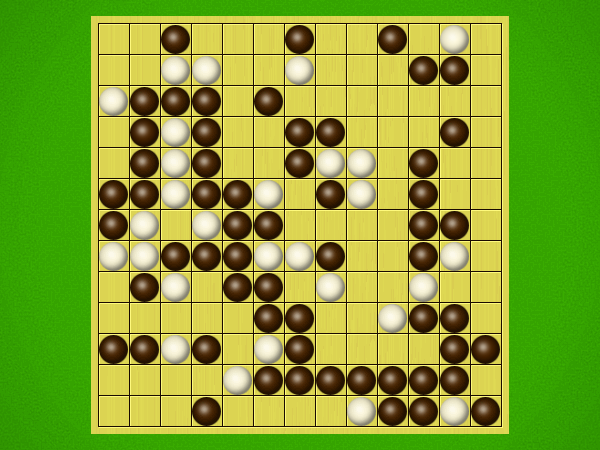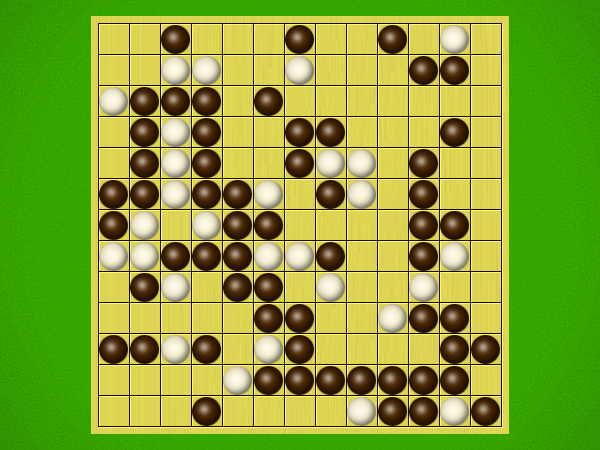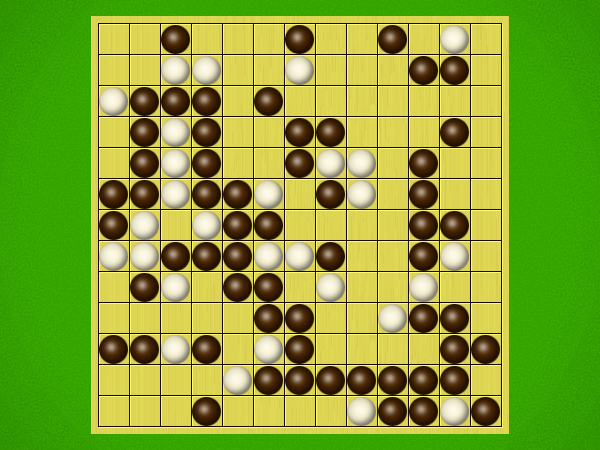
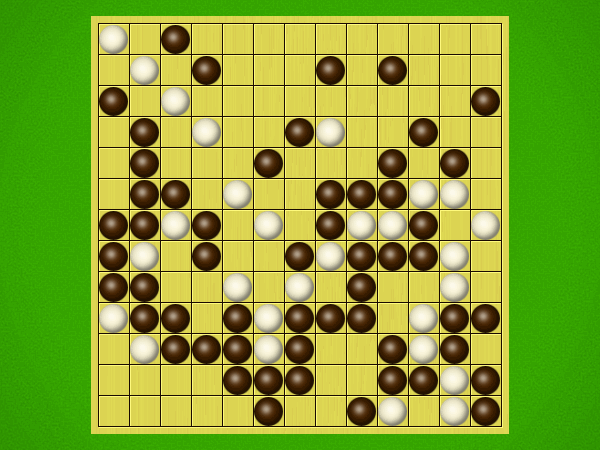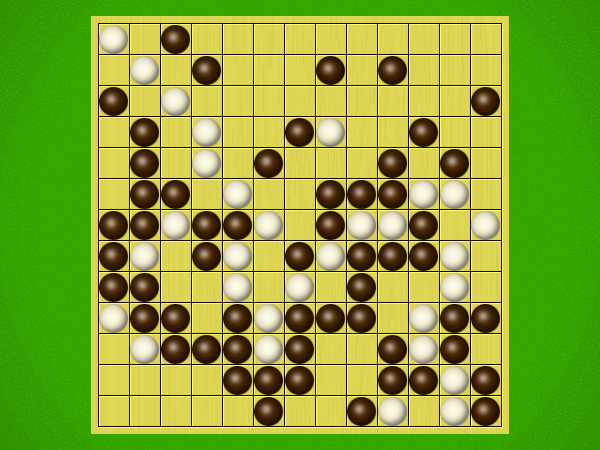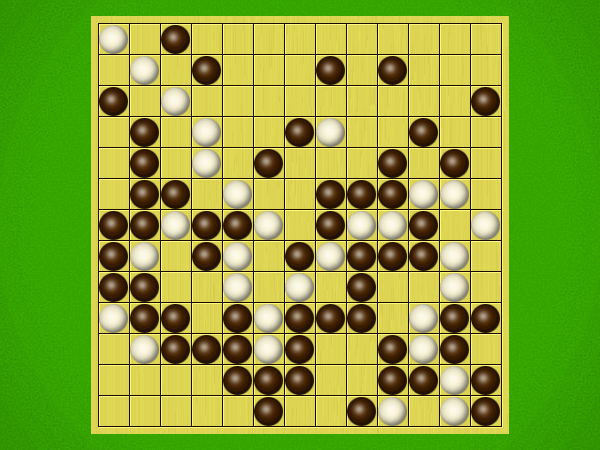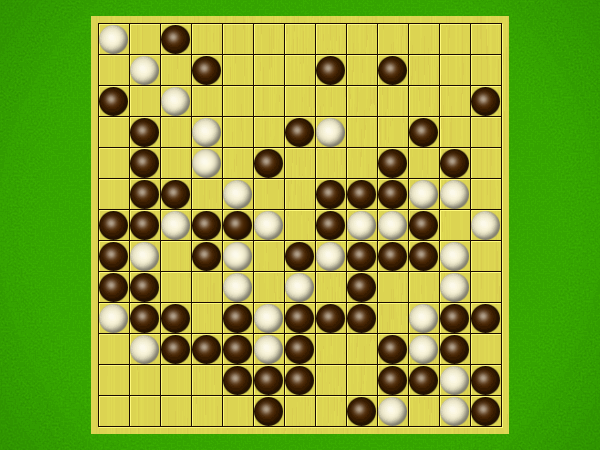
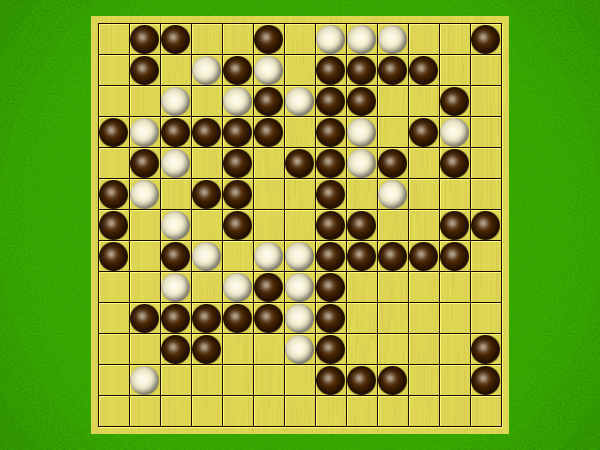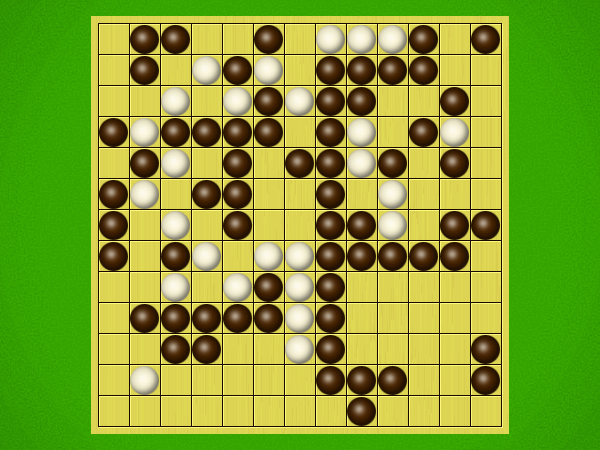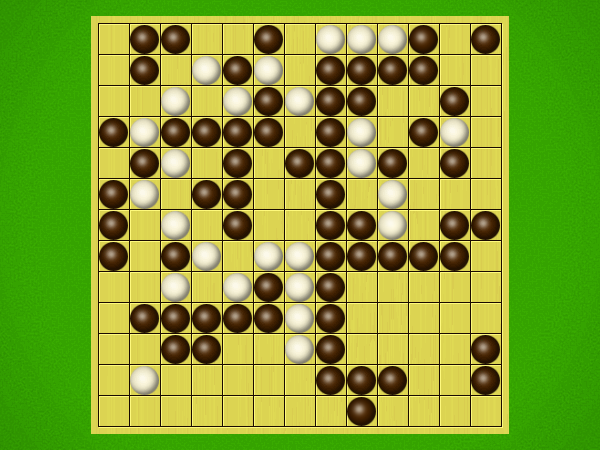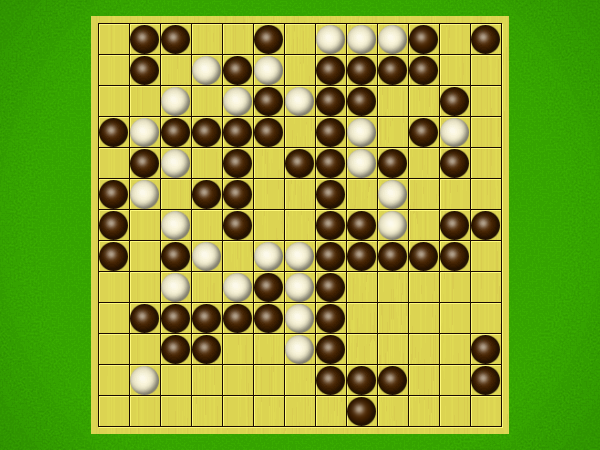
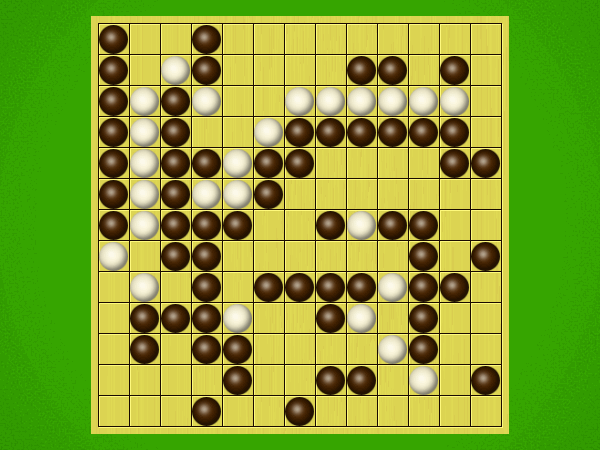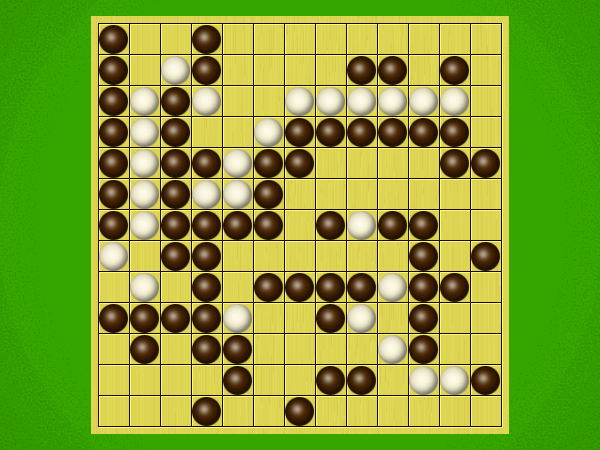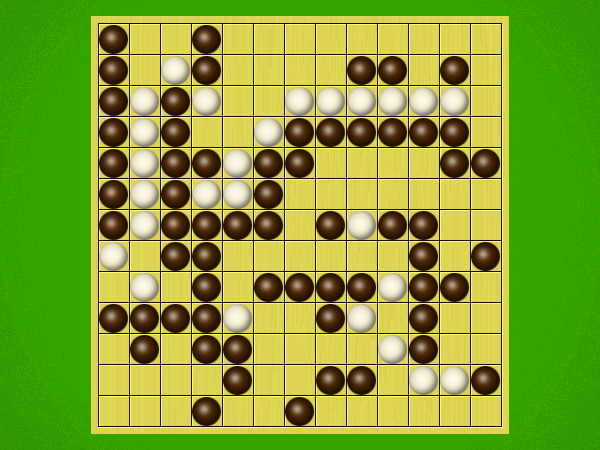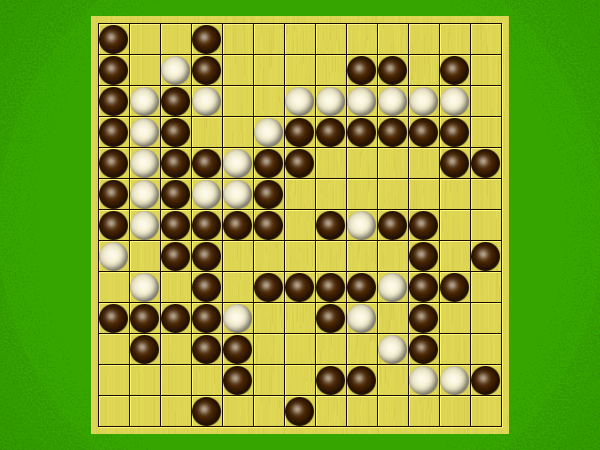
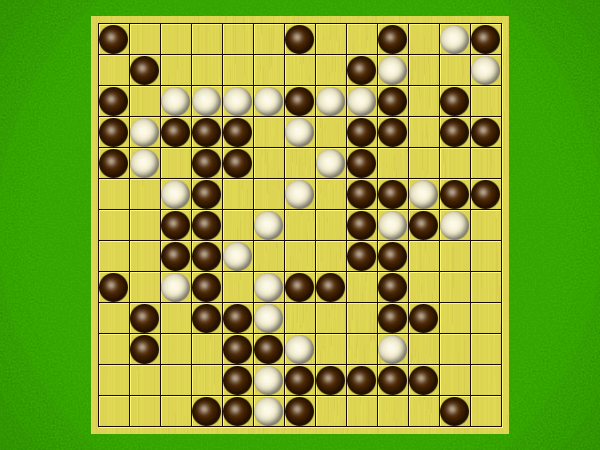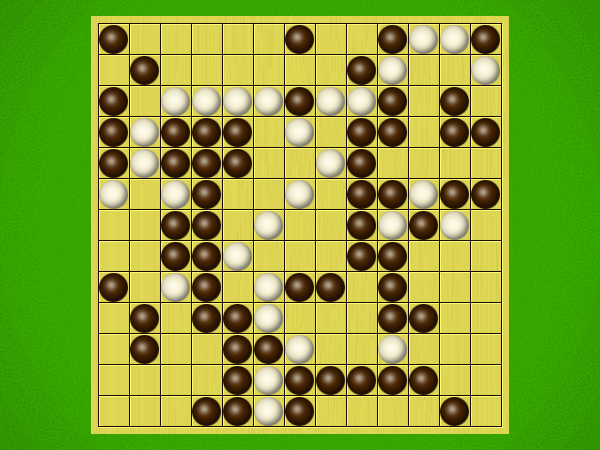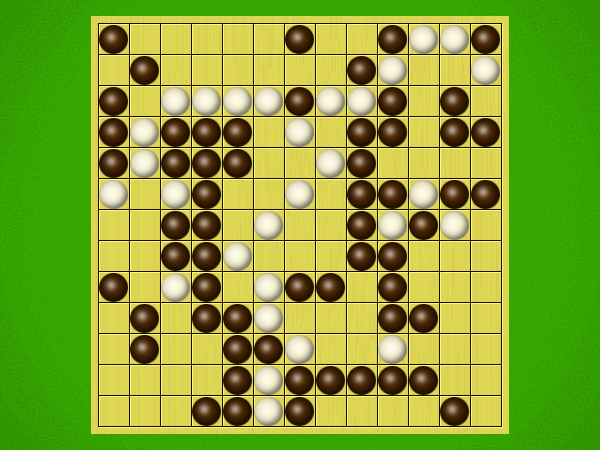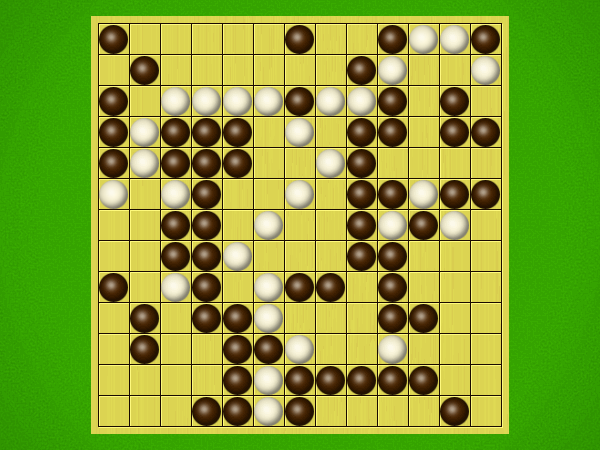
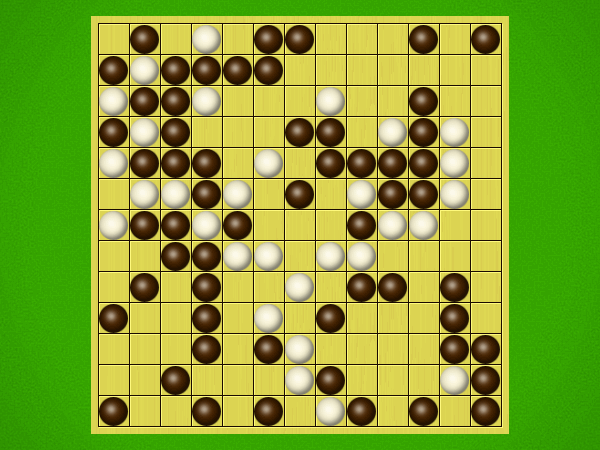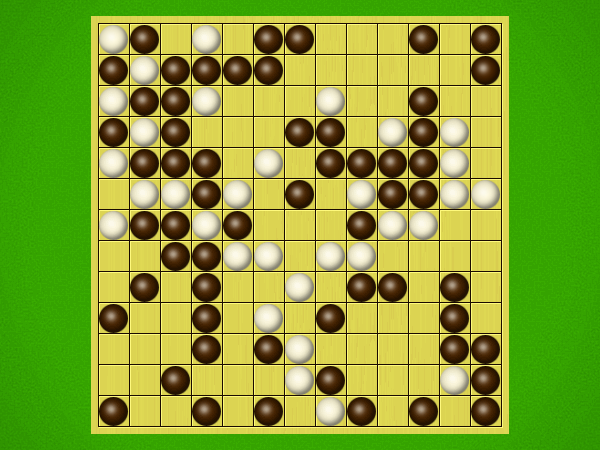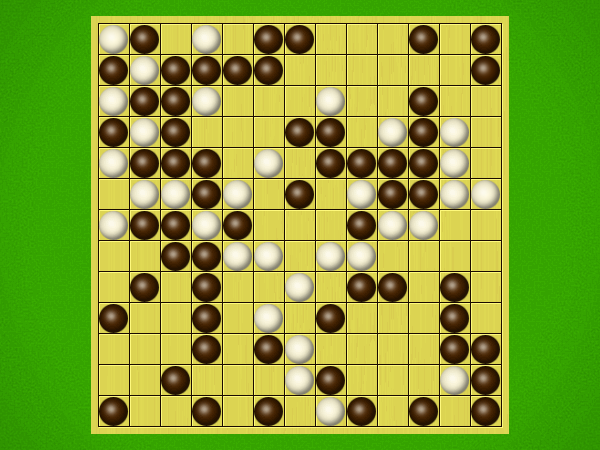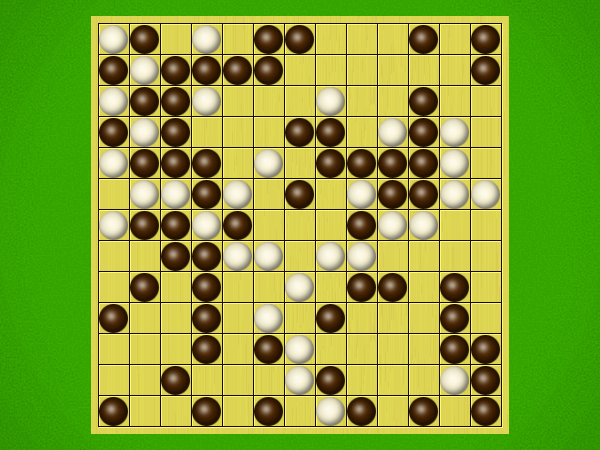
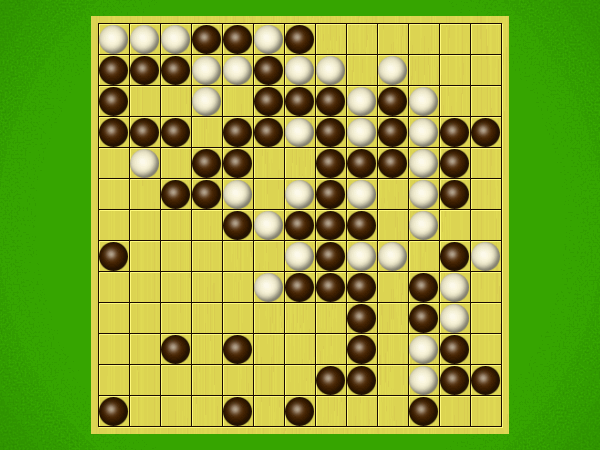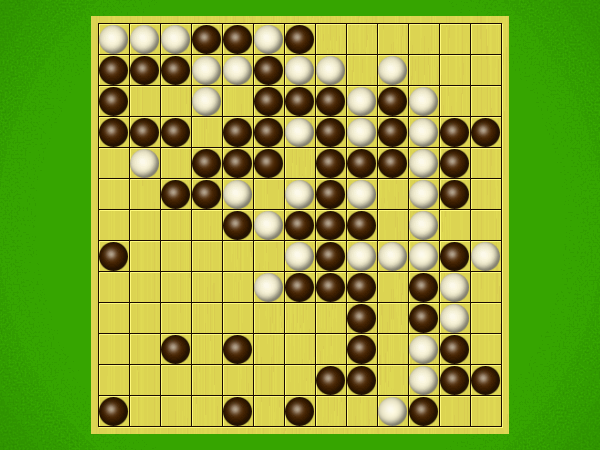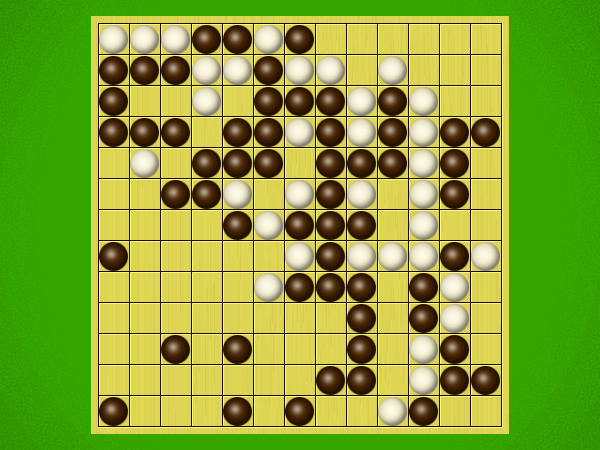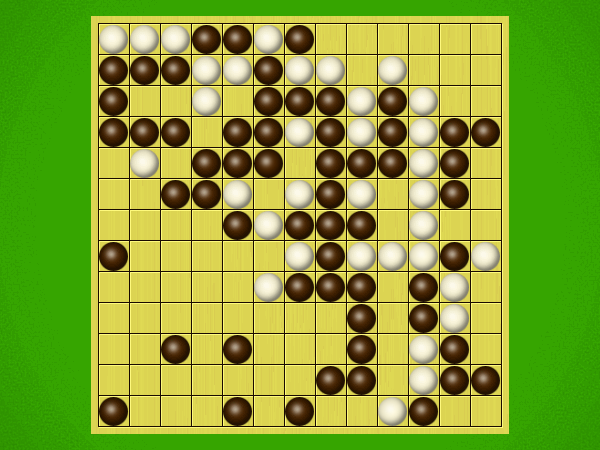
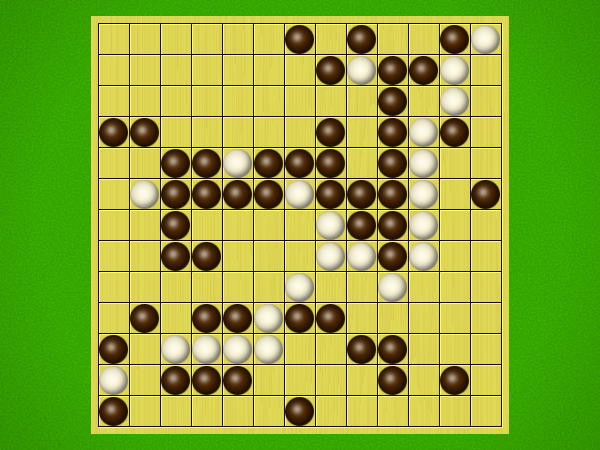
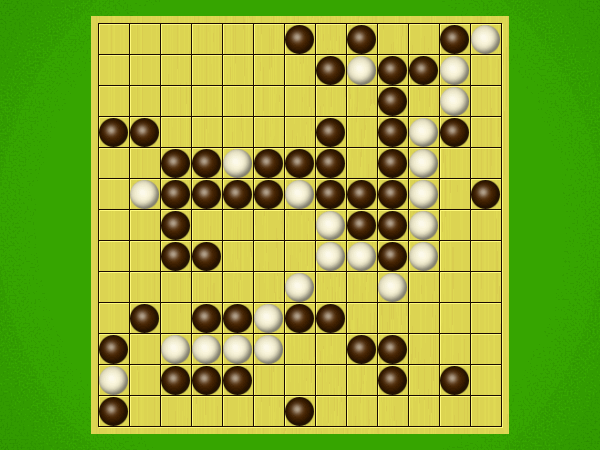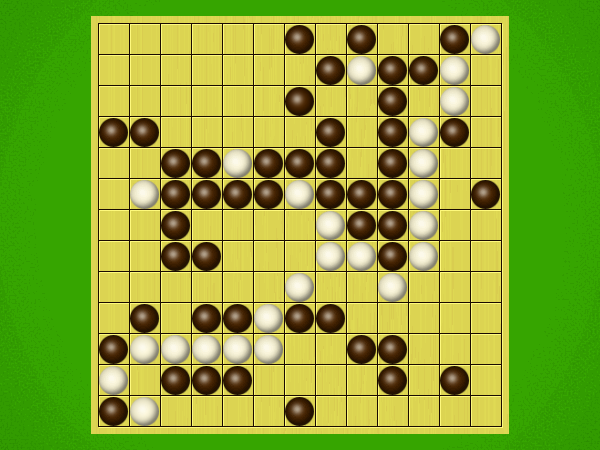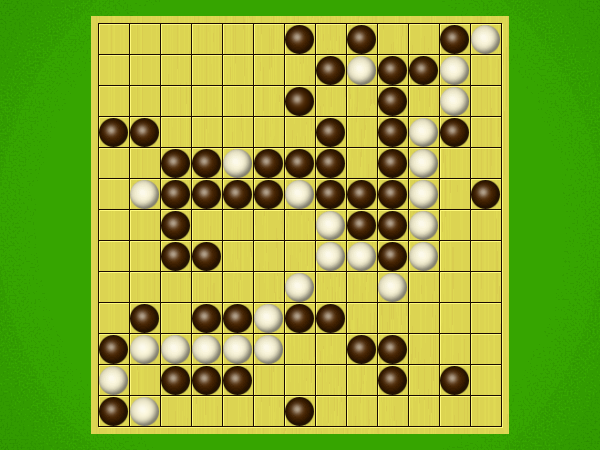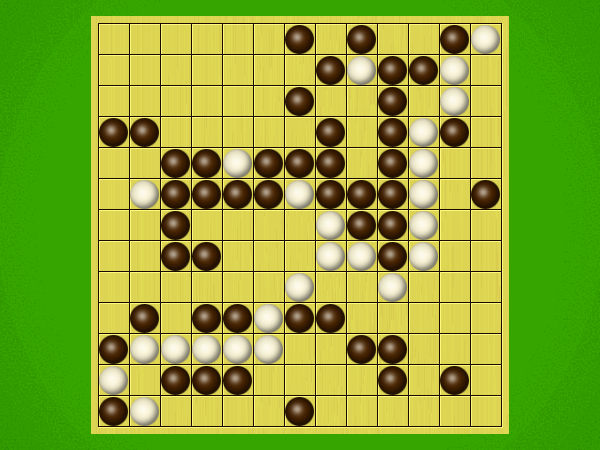
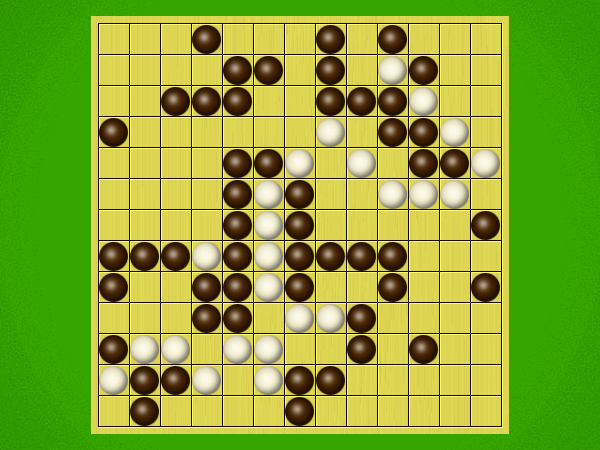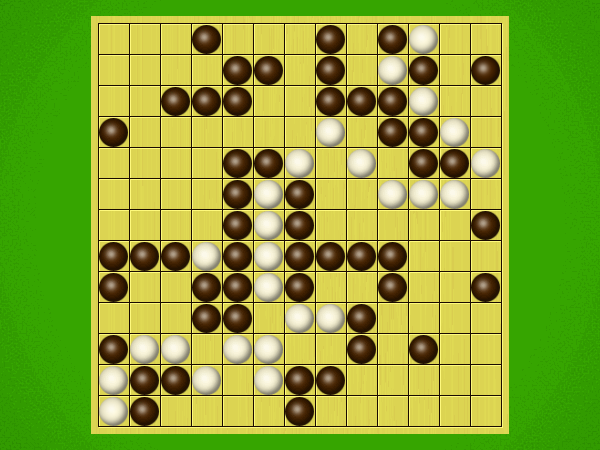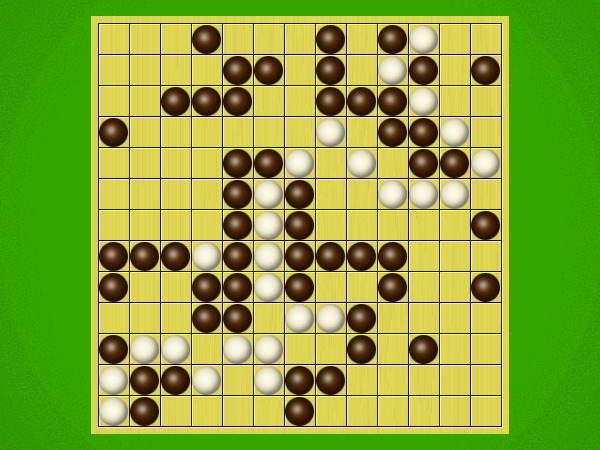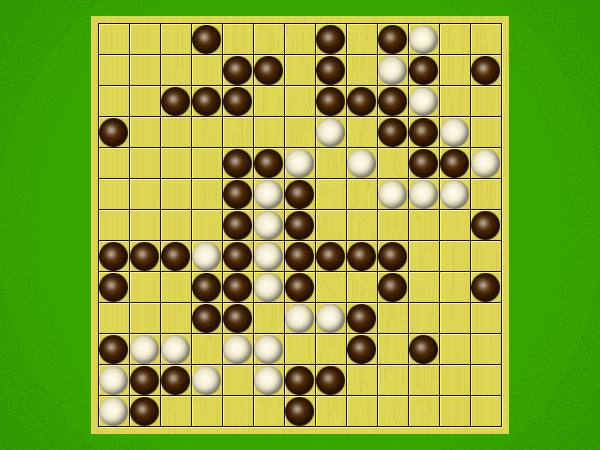
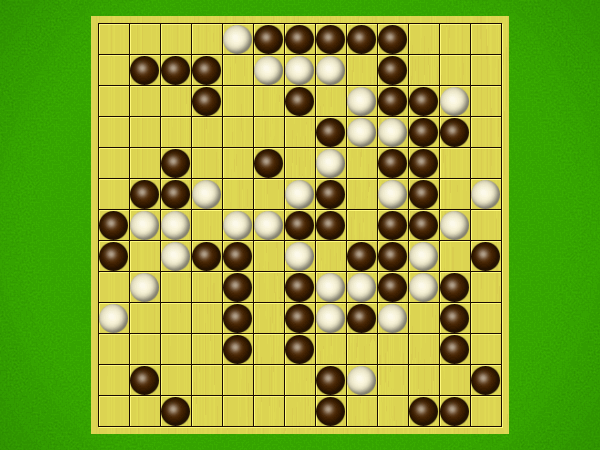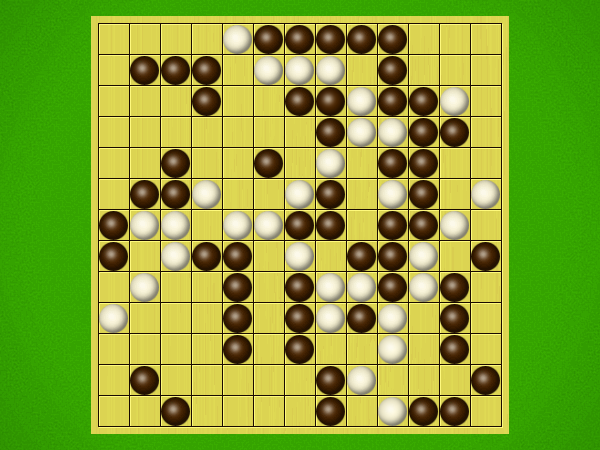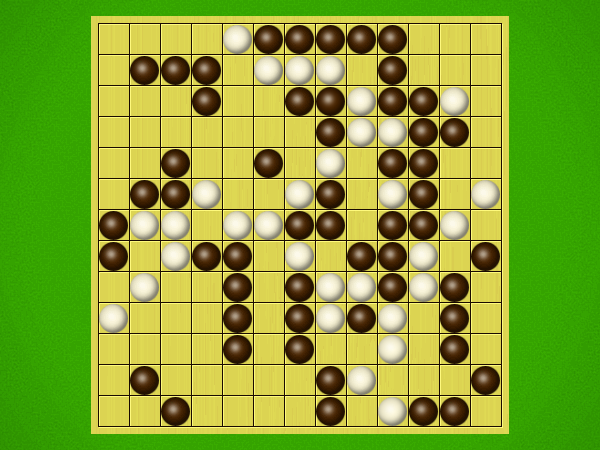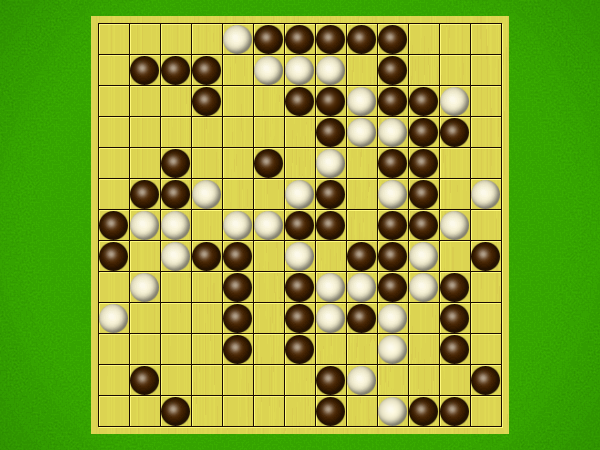
Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!
THE BASIC IDEA
The game begins with an auction phase -- a sort of mini-game of chicken (reminiscent of the game Unlur), in which the board is gradually seeded with a growing number of initial stones. The auction phase determines who will play the role of "Pip" (using black stones) and who plays the role of "Zip" (using white stones).
After the auction phase ends and the roles are thereby determined, the players take turns playing stones of their color to the board. Play continues until a winning condition is reached. (Draws are impossible.) Pip wins by connecting any TWO opposite sides of the board via a chain of orthogonally-adjacent black stones. Zip wins connecting all FOUR sides of the board via a chain of 8-way-adjacent white stones. ("8-way-adjacent" = either orthogonally or diagonally adjacent.)
IN MORE DETAIL
There are two varieties of play, "Zipline" and "Pipline".Pipline
The game begins with an "auction phase." In this phase, on his/her turn a player places 1-3 BLACK stones on the board. (Each player has a free choice of whether to place 1 black stone, or 2 black stones, or 3 black stones on his/her turn.) Players alternate turns, playing black stones exclusively in this phase of the game, until one player on his/her turn says "take" instead of placing any stones. This taker is henceforth known as "Pip" and will play a SINGLE black stone on each future turn. The opponent is "Zip," who will play a SINGLE white stone on each future turn.Immediately after "take" is announced, the non-taker (i.e. Zip) has his/her turn and places a single white stone, followed by a single black stone from Pip, then a single white stone from Zip, etc. Turns alternate in this fashion until one player achieves his/her win condition (or until one player resigns). Zip wins by connecting all FOUR sides of the board with a chain of white stones that are orthogonally and/or diagonally adjacent; Pip wins by connecting any TWO opposite sides with a chain of black stones that are orthogonally adjacent.
Zipline
This is an alternative version of the game. To start the game, on each turn a player places 1-3 WHITE stones in the auction phase. (Each player has a free choice of whether to place 1 white stone, or 2 white stones, or 3 white stones on his/her turn.) Players alternate turns, playing white stones exclusively in this phase of the game, until one player on his/her turn says "take" instead of placing any stones. This taker is henceforth known as "Zip" and on future turns Zip will play a SINGLE white stone per turn. The opponent is known as "Pip." On future turns, Pip will play TWO black stones per turn, with the following restriction: Pip's second black stone of a given turn is NOT allowed to be placed orthogonally adjacent to the first black stone of the turn. (Placing two diagonally adjacent black stones in the same turn IS allowed. Also, note that in the extremely rare case where ALL remaining empty cells are orthogonally adjacent to first black stone, the second black stone is forfeited.)
Immediately after "take" is announced, the non-taker (i.e. Pip) has his/her turn and plays two black stones, followed by a single white stone played by Zip, then two black stones from Pip, then a single white stone from Zip, etc. Turns alternate in this fashion until one player achieves his/her win condition (or until one player resigns). Zip wins by connecting all FOUR sides of the board with a chain of white stones that are orthogonally and/or diagonally adjacent; Pip wins by connecting any TWO opposite sides with a chain of black stones that are orthogonally adjacent.
NOTE: In either version of the game (Pipline or Zipline), if during the auction phase a player creates the win condition for the color being used in the auction, then that player wins the game. (However, this won't happen if both player play competently!)
Not implemented in Ai Ai: Zipline can also be played as a 3 player game. In 3 player Zipline, the taker plays as Zip and the two non-takers play as a single Pip team. Each non-taker plays a single black stone on his/her turn, for a total of two black stones for Pip for every one white stone for Zip. Roles are determined in the auction phase using the same process described for 3 player Unlur in this thread.
"Freestyle" Zipline Variant: For variety you can play with free placement for Pip's two black stones, that is, with no ban on orthogonally adjacent placements.