Full Report for Shrine by Alek Erickson

SHRINE is a competitive abstract strategy game, where two players take turns placing stones on a beautiful board of tiled pentacles.

Rules

RULES

The stones and the pentacles each come in three colors: crimson, cream, and cobalt.

Stone placement follows this order, and players take turns placing the next color of stone on the board.

There are only two rules to placement: no stone may be placed on a pentacle of its own color, and no two stones of the same color may be placed next to one another.

WINNING

Stones on pentacles sharing an interface are connected.
Connected stones, enclosing at least one pentacle, are a loop.
A loop that encloses at least one pentacle of each color is a shrine.
The player to complete the first shrine wins the game.

NOTES

Shrine is distinct from classic stone-placing games in that players become decoupled from colors.
A winning structure will usually include stones laid by both players, but the winner is the one who places the final stone.
This leads to an interesting dilemma: how much do I cooperate with my opponent to build this shrine?

Miscellaneous

General comments:

Play: Combinatorial

Family: Combinatorial 2017

Mechanism(s): Pattern,Strict Placement

BGG Stats

BGG Entry	Shrine
BGG Rating	5.75
#Voters	4
SD	2.86138
BGG Weight	0
#Voters	0
Year	2017

BGG Ratings and Comments

User	Rating	Comment
alekerickson	10
Earth Dragon	5
mrraow	6	Very hard to read ahead in this game mostly due to the unusual topology; but I can see that if I played enough, there is quite a lot of strategy here. Note: although the board looks like it has 5-fold connectedness, it's actually implemented with 7 connections per cell in Ai Ai.
Kaffedrake	2	An exercise in reading an increasingly convoluted game state to the point where accumulated move restrictions and the colour play sequence exclusively allow you to satisfy the win condition. Most of the time before this happens you can play randomly and it will have no practical effect on the outcome.

Levels of Play

AI	Strong Wins	Draws	Strong Losses	#Games	Strong Win%	p1 Win%	Game Length
Random
Grand Unified UCT(U1-T,rSel=s, secs=0.01)	36	0	0	36	100.00	52.78	73.28
Grand Unified UCT(U1-T,rSel=s, secs=0.07)	36	0	9	45	80.00	46.67	71.24

Level of Play: Strong beats Weak 60% of the time (lower bound with 90% confidence).

Draw%, p1 win% and game length may give some indication of trends as AI strength increases; but be aware that the AI can introduce bias due to horizon effects, poor heuristics, etc.

Kolomogorov Complexity Estimate

Size (bytes)	27684
Reference Size	10293
Ratio	2.69

Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.

Playout Complexity Estimate

Playouts per second	4247.40 (235.44µs/playout)
Reference Size	311026.22 (3.22µs/playout)
Ratio (low is good)	73.23

Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.

Win % By Player (Bias)

1: White win %	49.10±3.09	Includes draws = 50%
2: Black win %	50.90±3.10	Includes draws = 50%
Draw %	0.00	Percentage of games where all players draw.
Decisive %	100.00	Percentage of games with a single winner.
Samples	1000	Quantity of logged games played

Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)

Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.

Playout/Search Speed

class="footnote">Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.

Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.

Mirroring Strategies

Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.

Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.

Complexity

Label	Its/s	SD	Nodes/s	SD	Game length	SD
Random playout	4,356	380	336,948	29,289	77	6
search.UCB	4,425	294			69	6
search.UCT	4,495	297			68	5

Game length	68.45
Branching factor	41.48
Complexity	10^104.26	Based on game length and branching factor
Samples	1000	Quantity of logged games played

Move Classification

Distinct actions	125	Number of distinct moves (e.g. "e4") regardless of position in game tree
Good moves	51	A good move is selected by the AI more than the average
Bad moves	73	A bad move is selected by the AI less than the average
Samples	1000	Quantity of logged games played

Change in Material Per Turn

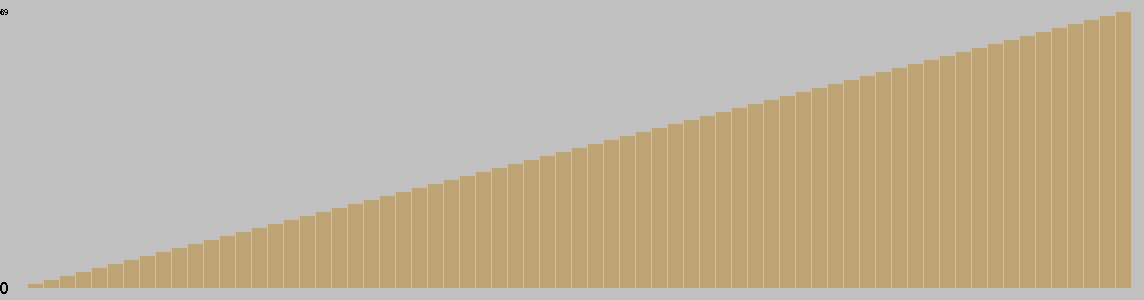
This chart is based on a single playout, and gives a feel for the change in material over the course of a game.

Trajectory

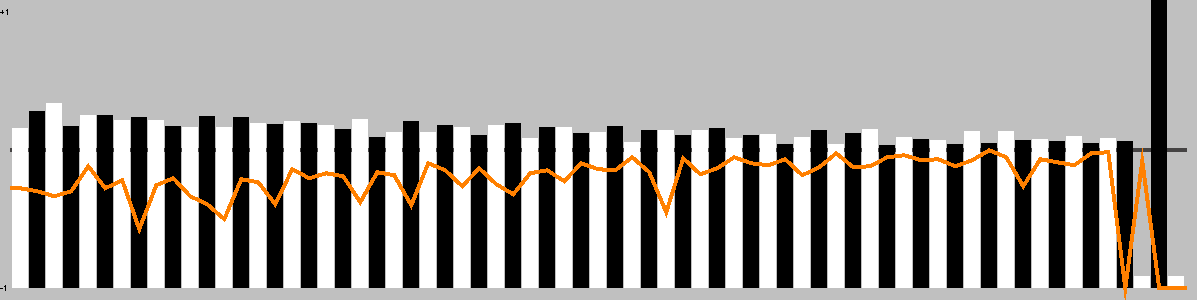
This chart shows the best move value with respect to the active player; the orange line represents the value of doing nothing (null move).

The lead changed on 65% of the game turns. Ai Ai found 10 critical turns (turns with only one good option).

Overall, this playout was 95.65% hot.

Position Heatmap

This chart shows the relative temperature of all moves each turn. Colour range: black (worst), red, orange(even), yellow, white(best).

Actions/turn

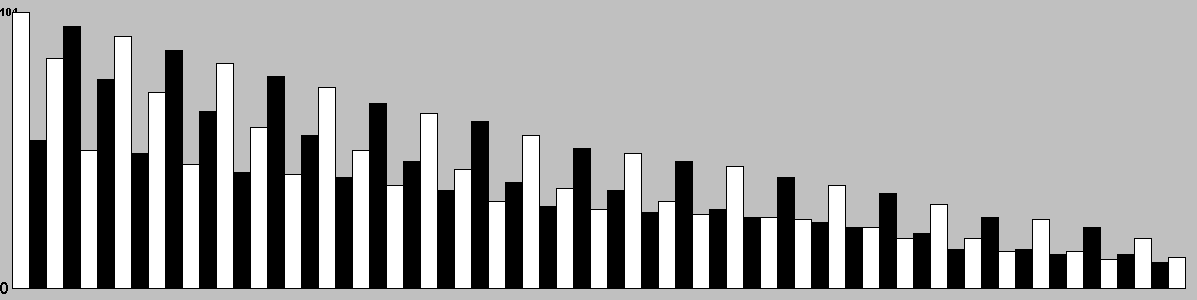
Table: branching factor per turn.

Action Types per Turn

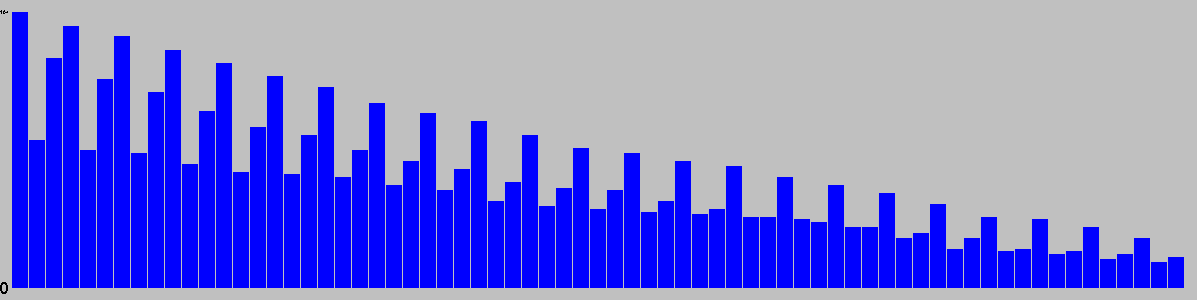
This chart is based on a single playout, and gives a feel for the types of moves available over the course of a game.

Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.

Unique Positions Reachable at Depth

0	1	2	3
1	104	5892	509348

Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.

Shortest Game(s)

No solutions found to depth 3.

Openings

Moves	Animation
f1E,g7N,c8W
b5E,h4N,b2N
b8S,h5W,f6N
b2S,f6N
c2W,e1N
e2E,a7N
a3S,e6W
a3N,e6W
b3E,f2S
h3E,b4N
b4S,g8E
e5N,h1W

Puzzles

Puzzle	Solution
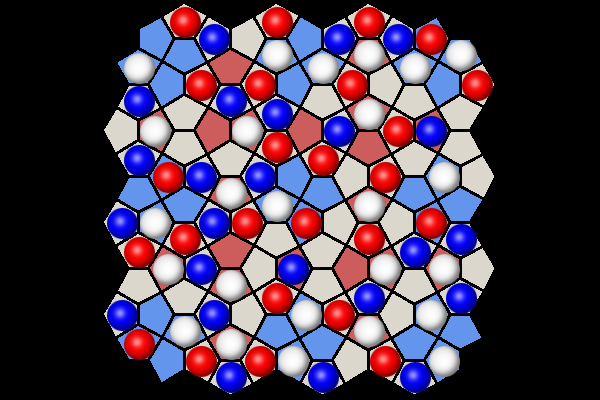White to win in 7 moves
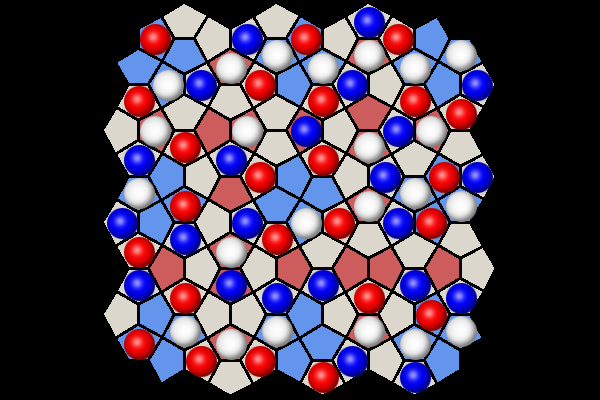White to win in 3 moves
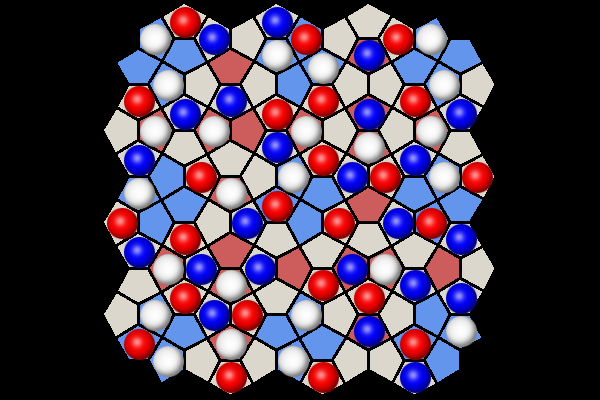Black to win in 5 moves
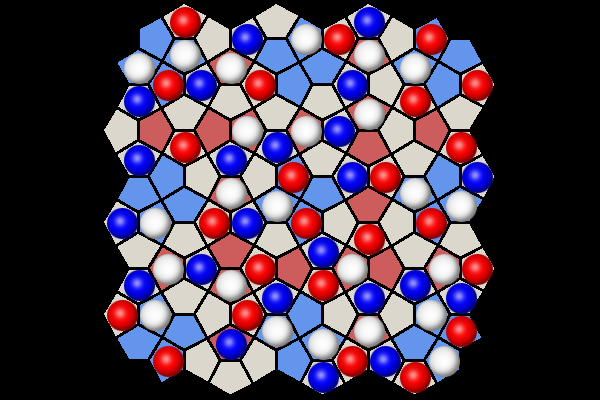Black to win in 3 moves
White to win in 6 moves
White to win in 7 moves

Selection criteria: first move must be unique, and not forced to avoid losing. Beyond that, Puzzles will be rated by the product of [total move]/[best moves] at each step, and the best puzzles selected.