Rules
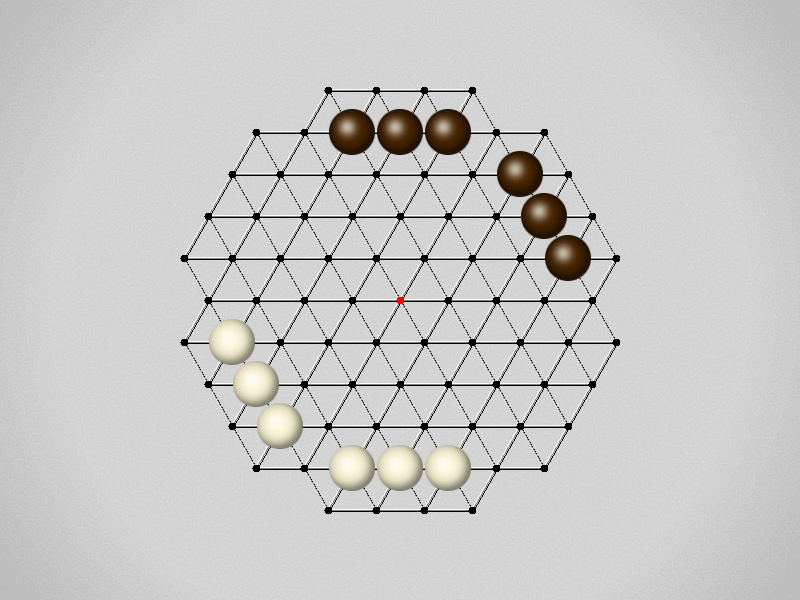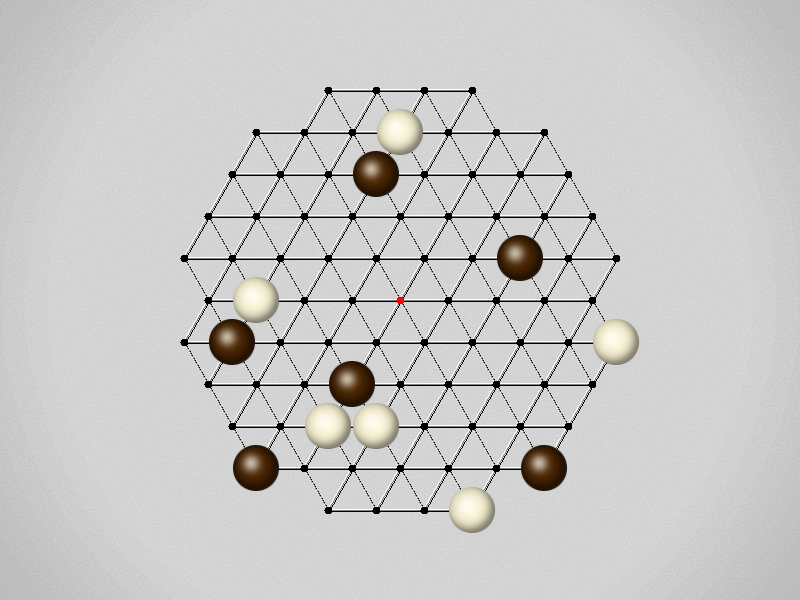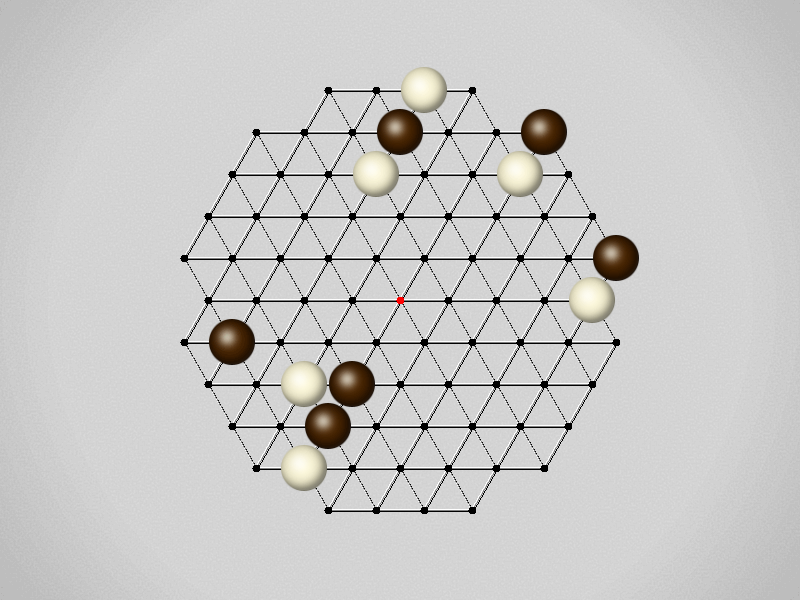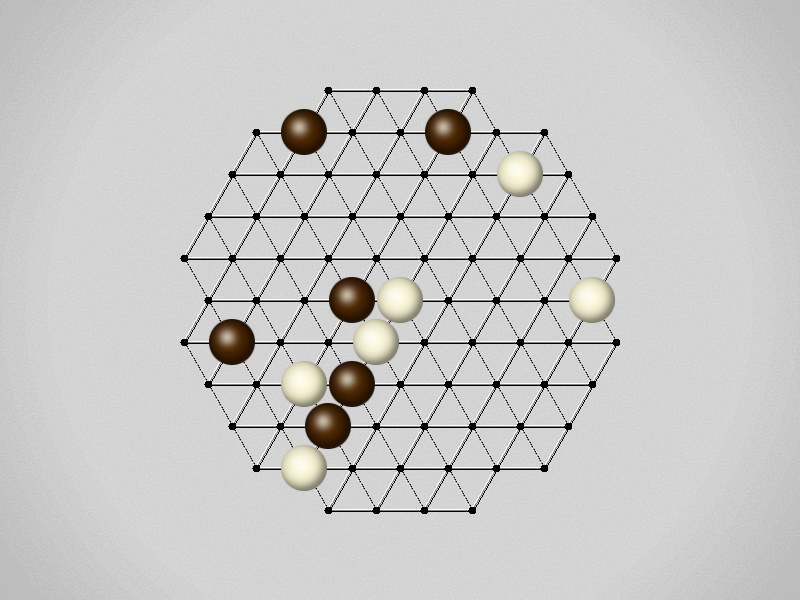
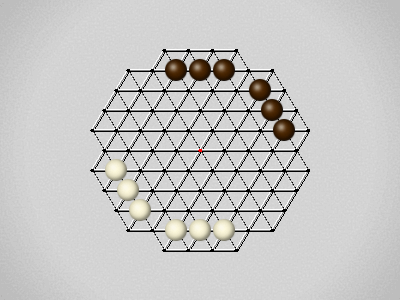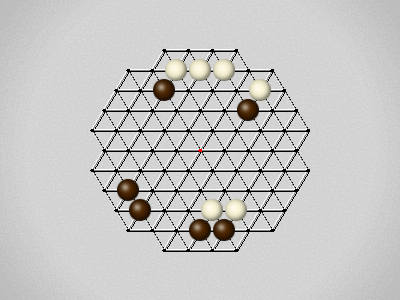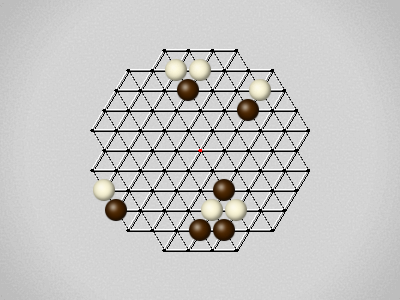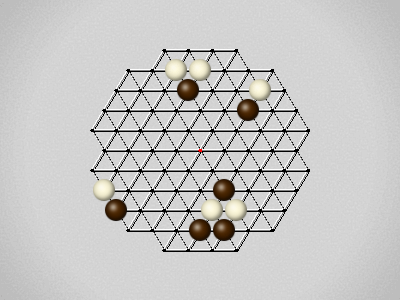
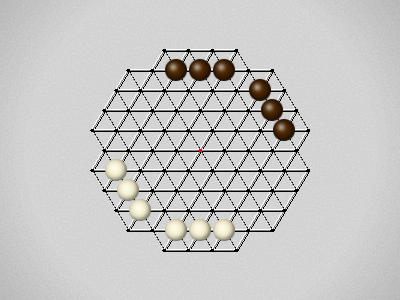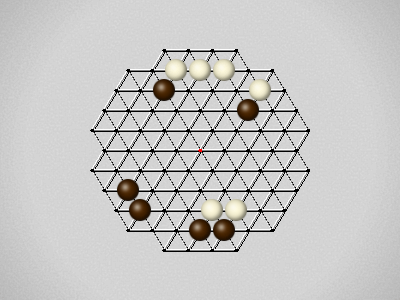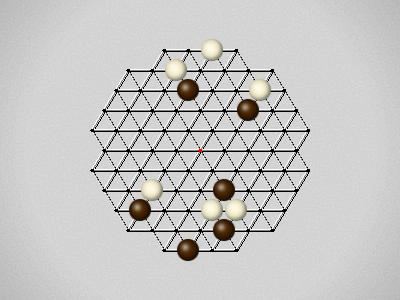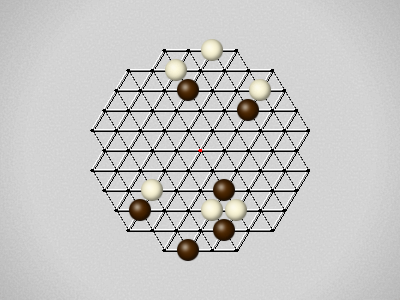
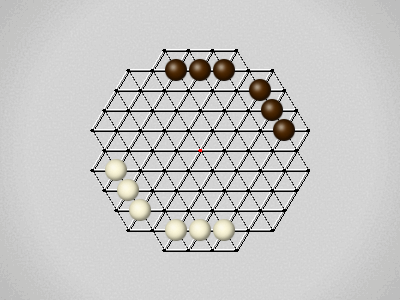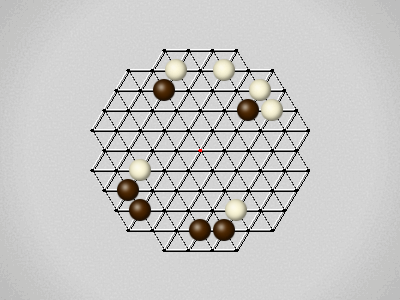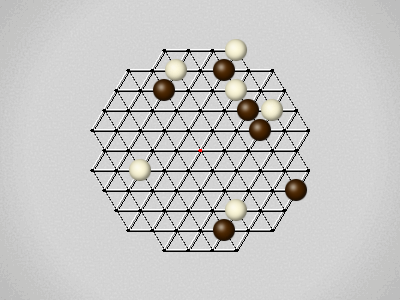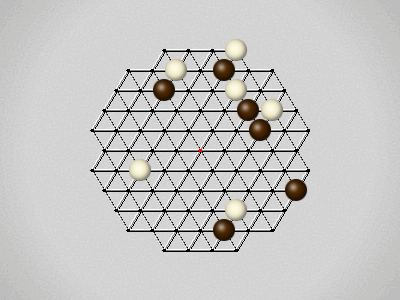
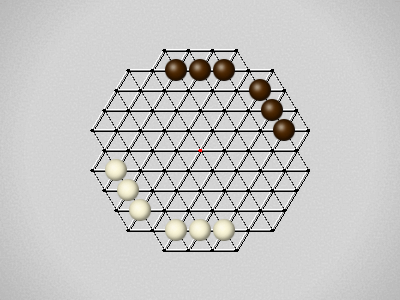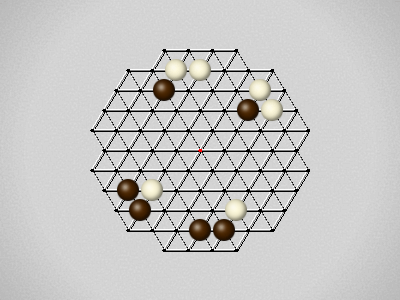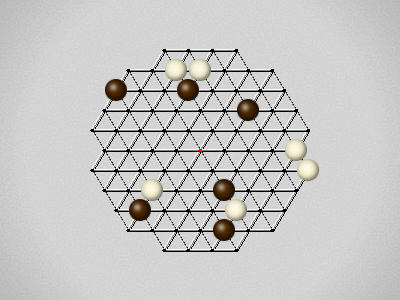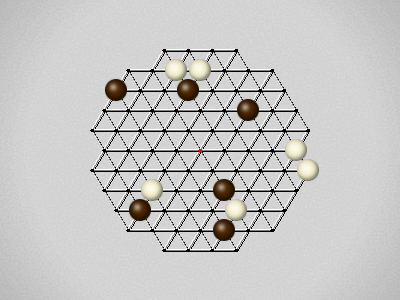
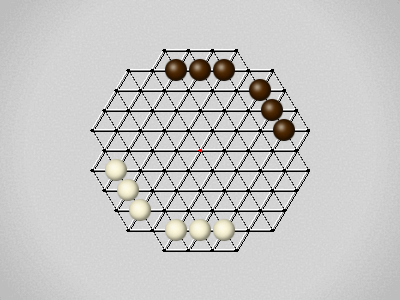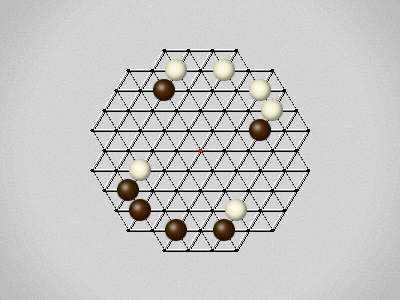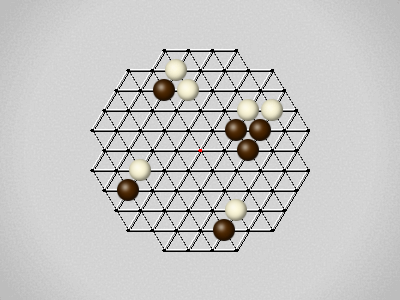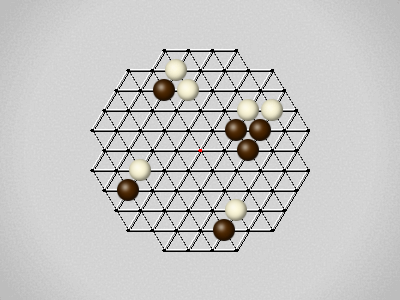
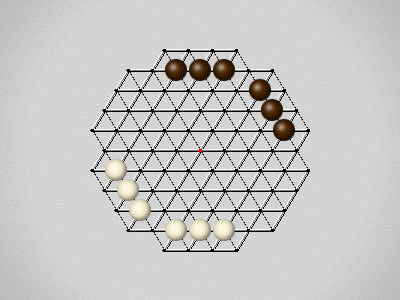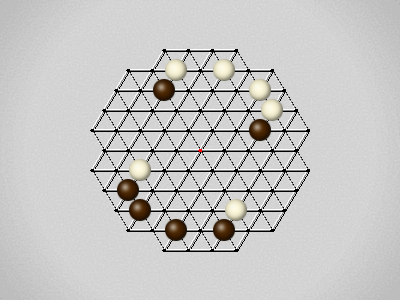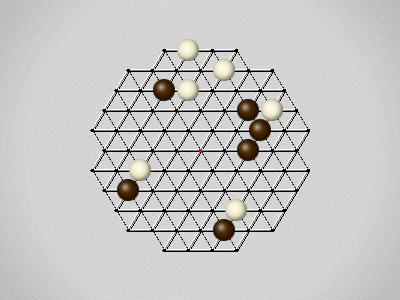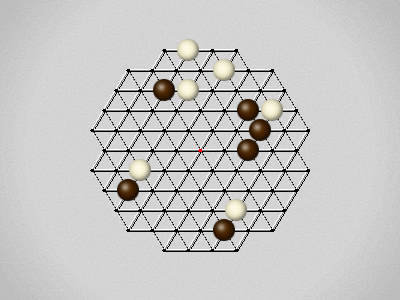
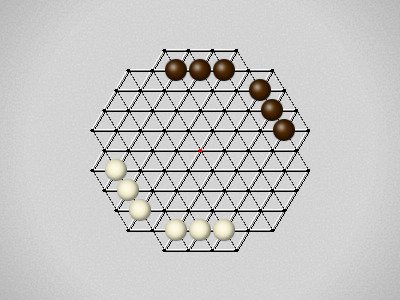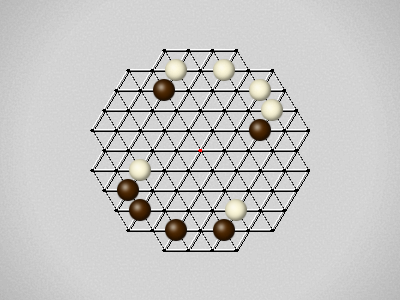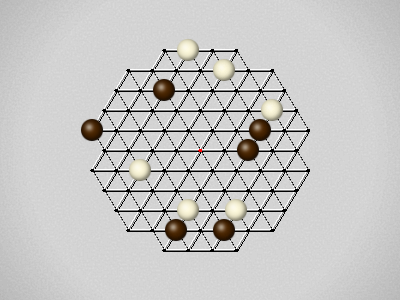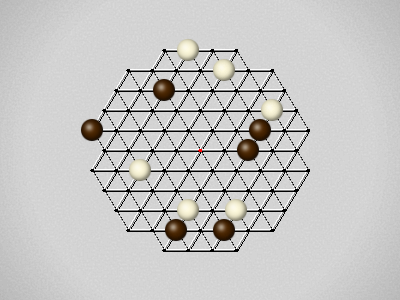
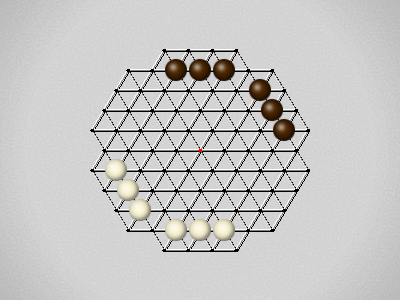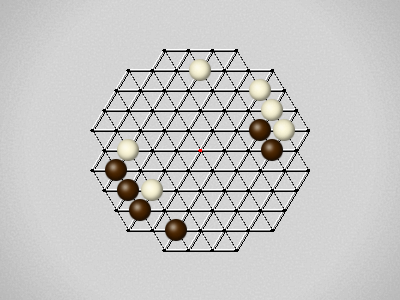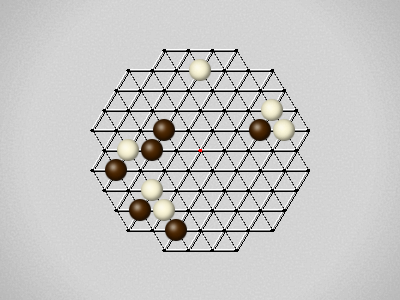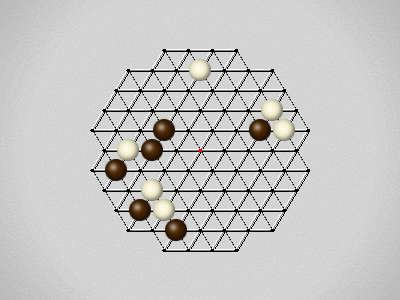
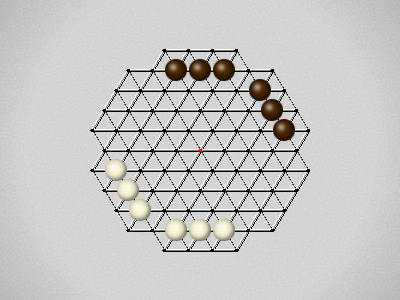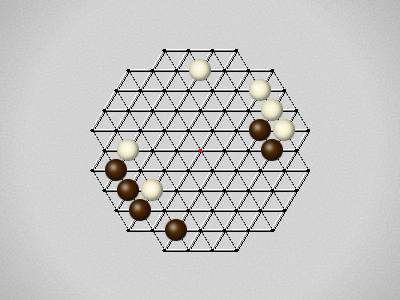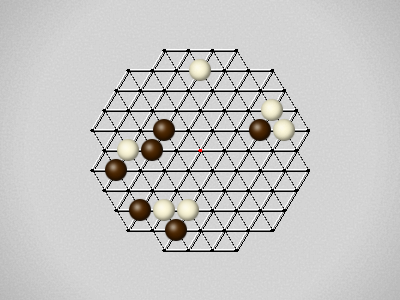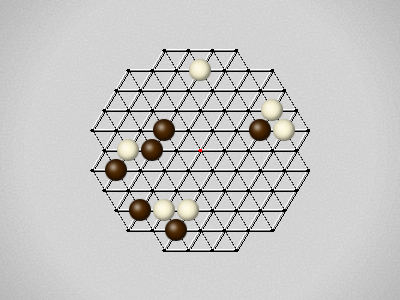
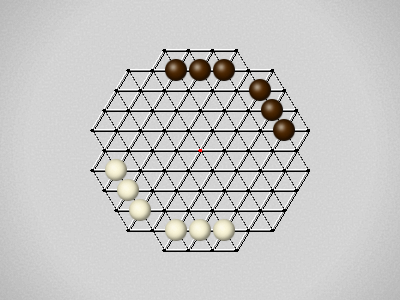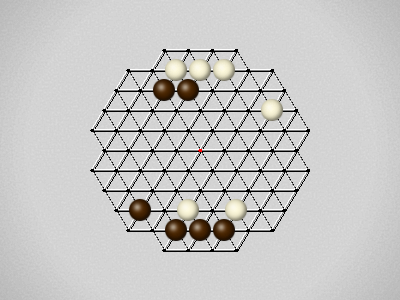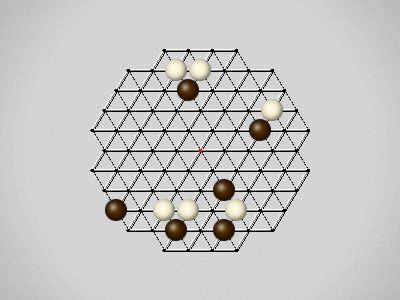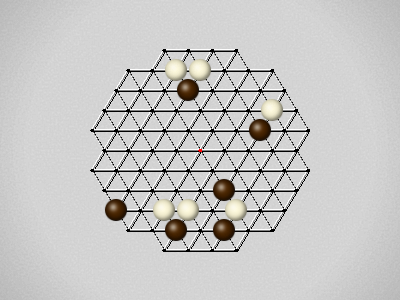
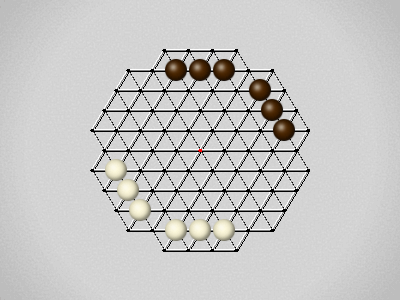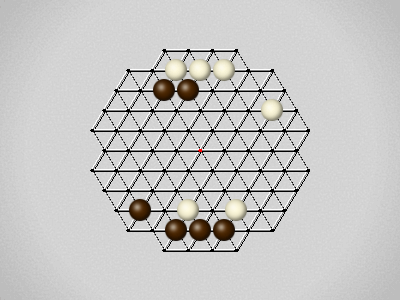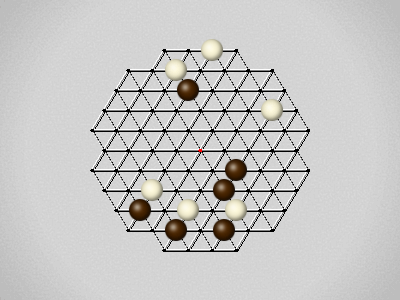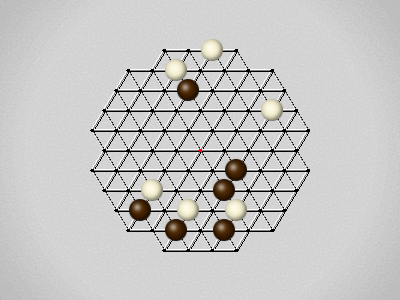
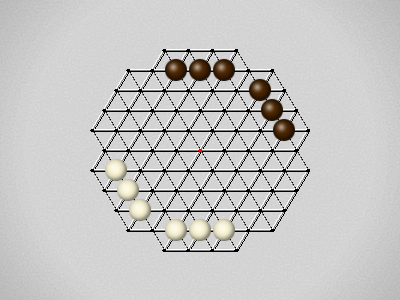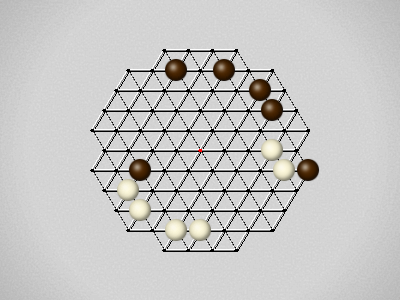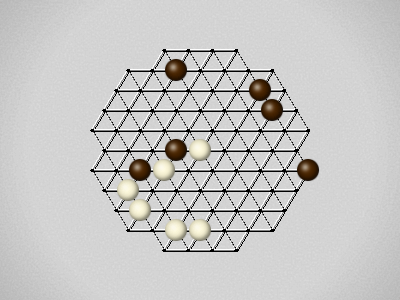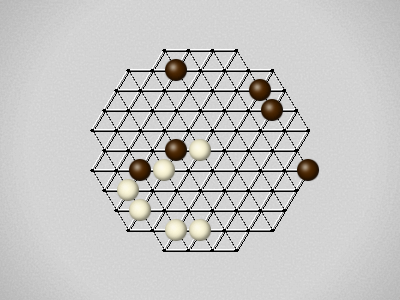
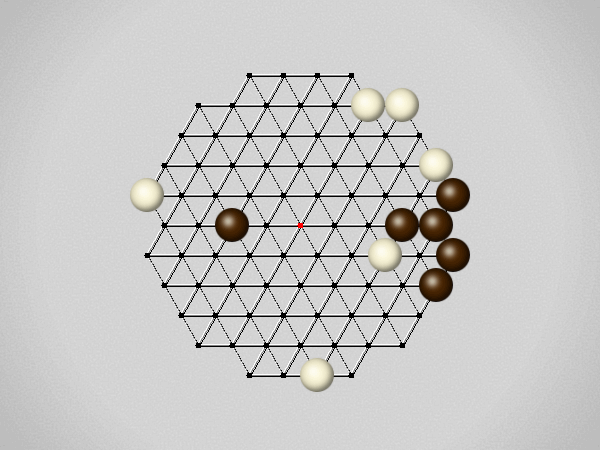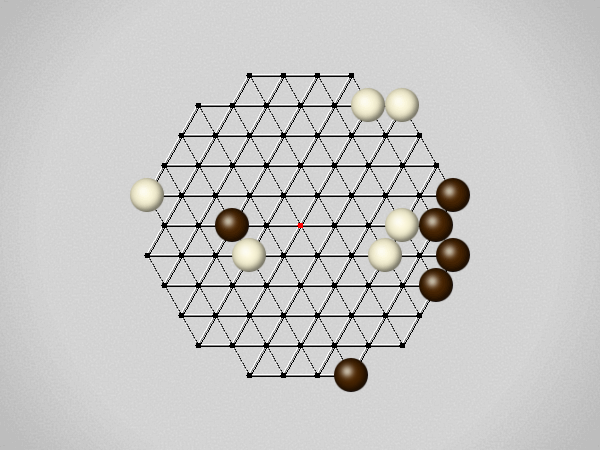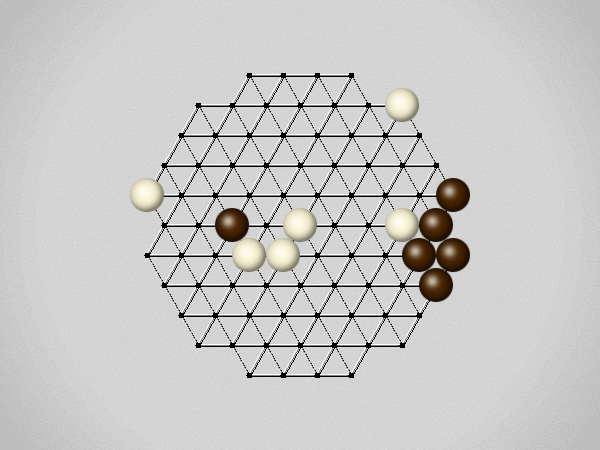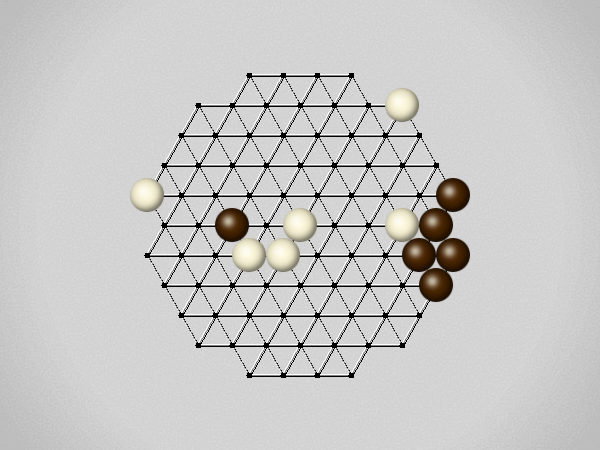
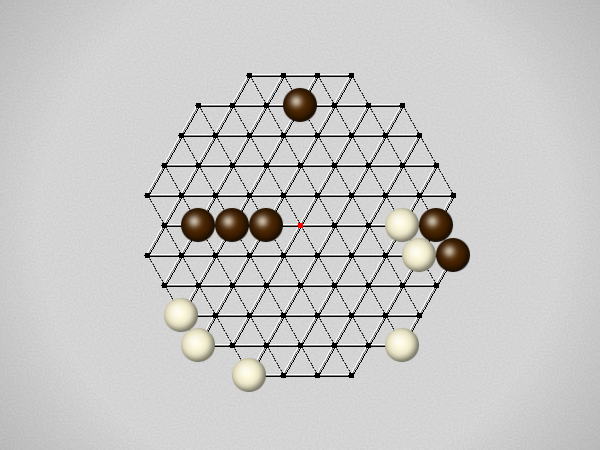
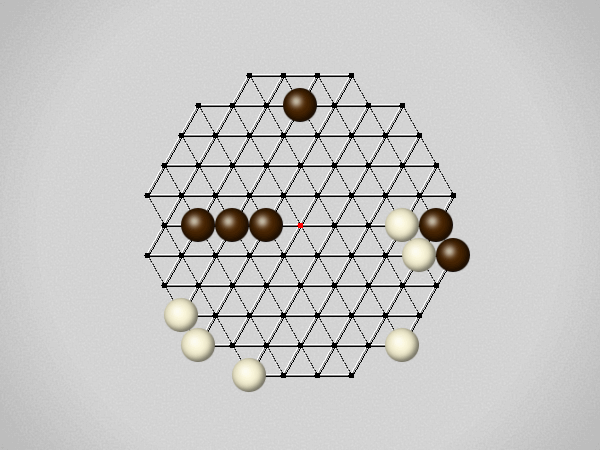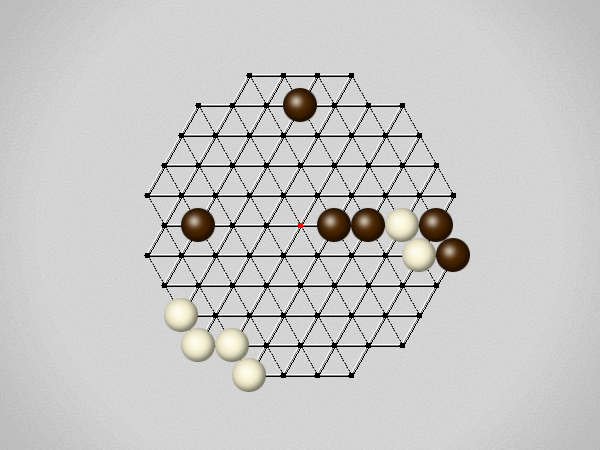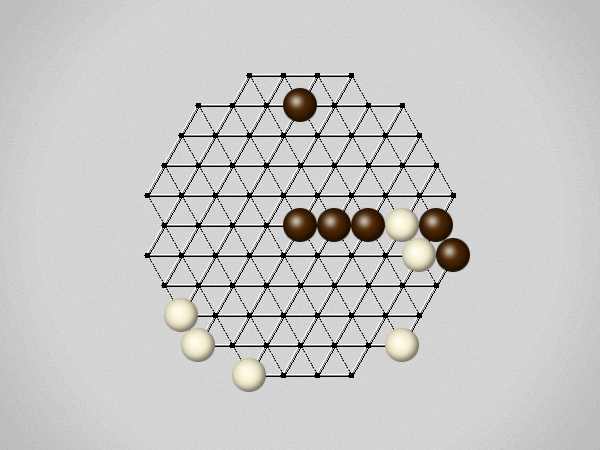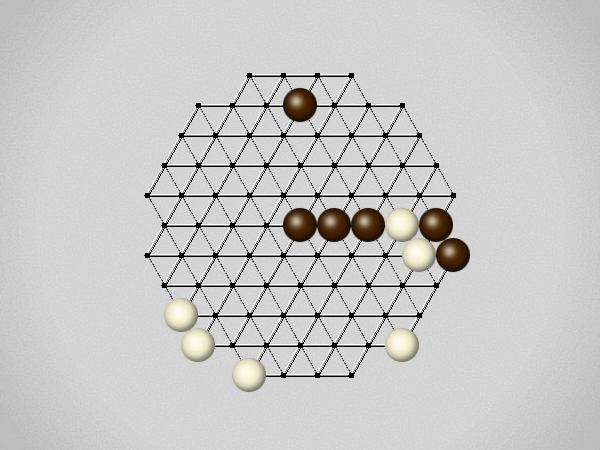
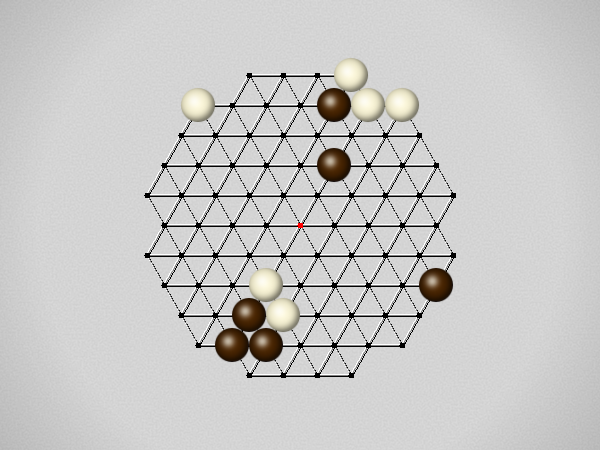
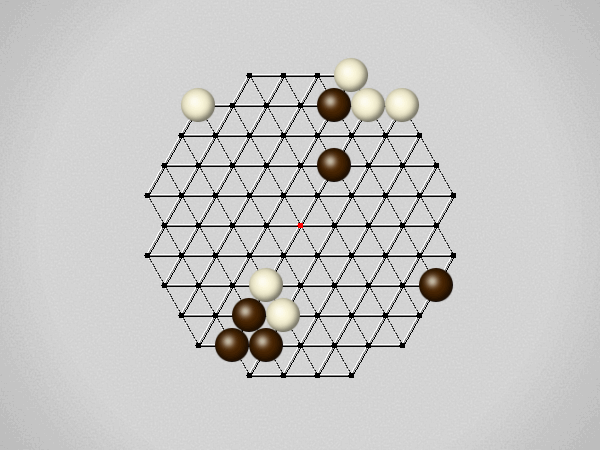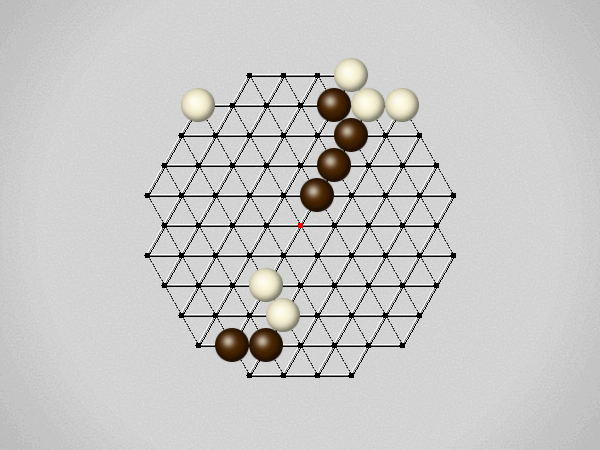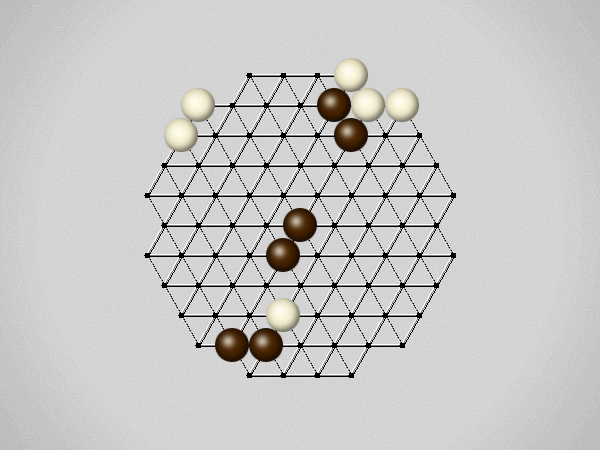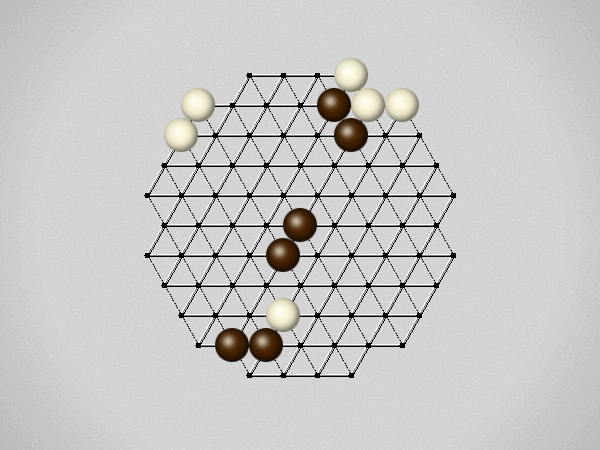
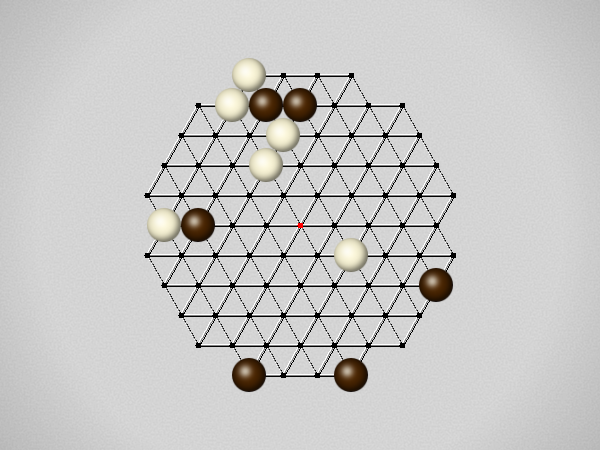
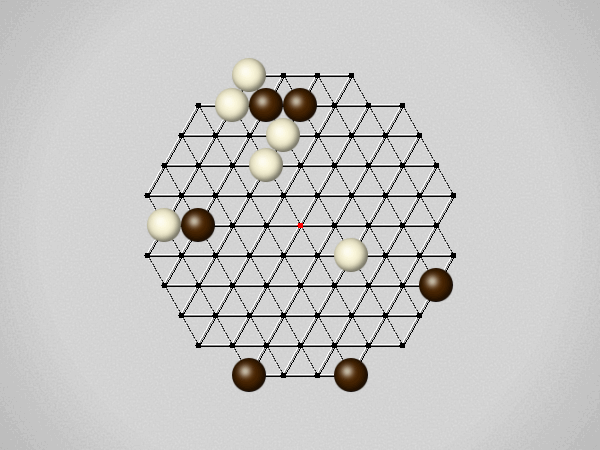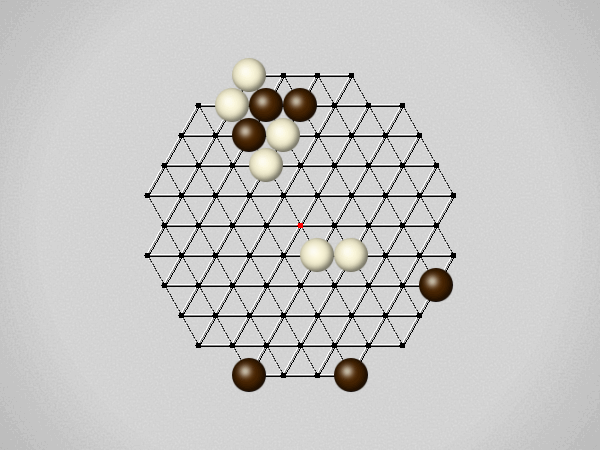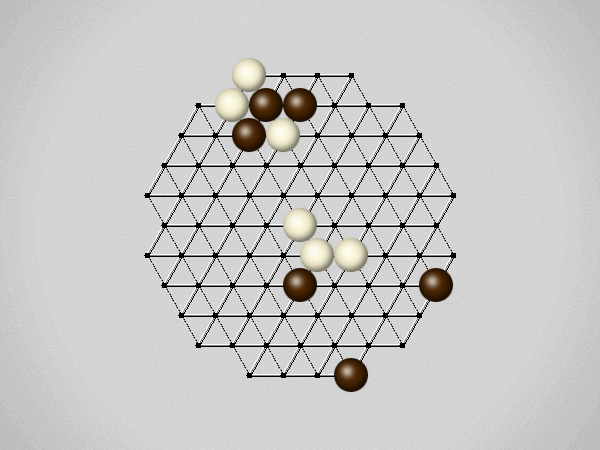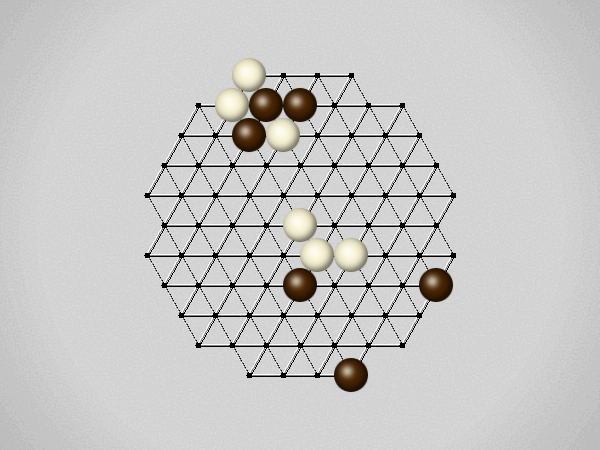
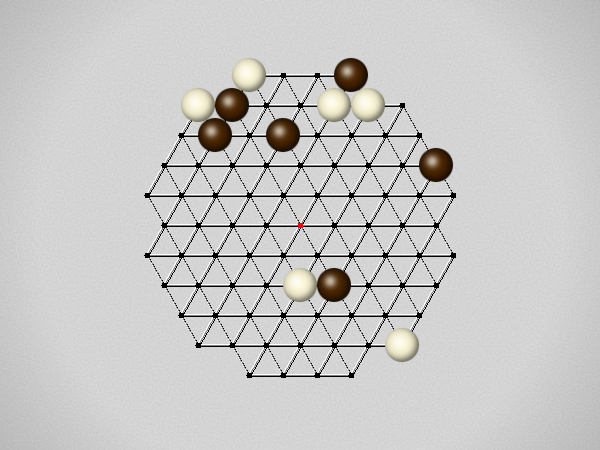
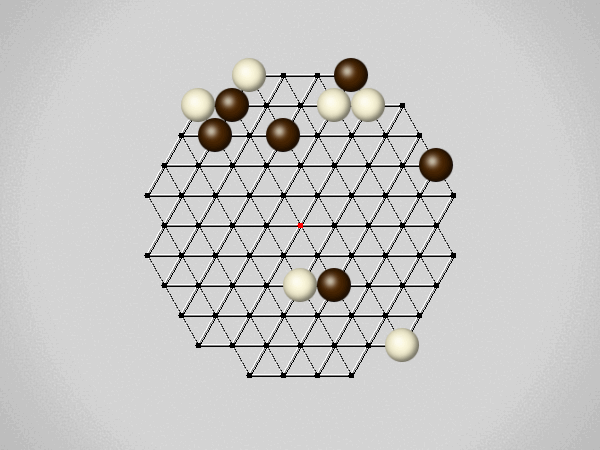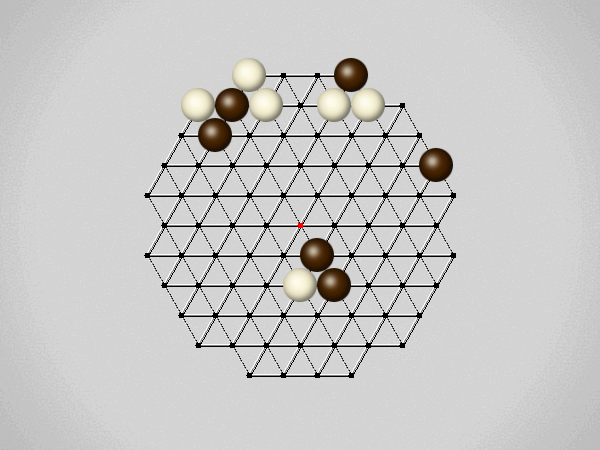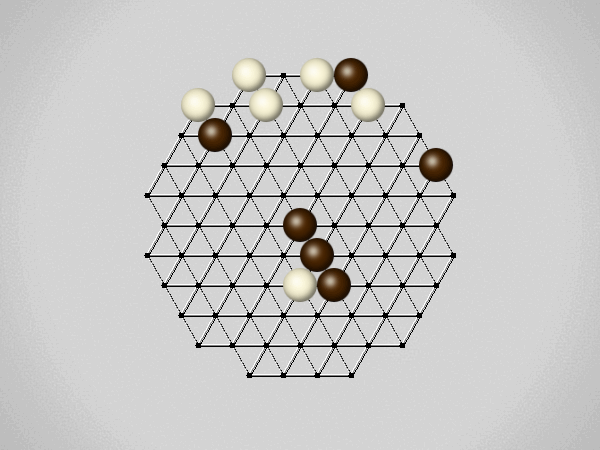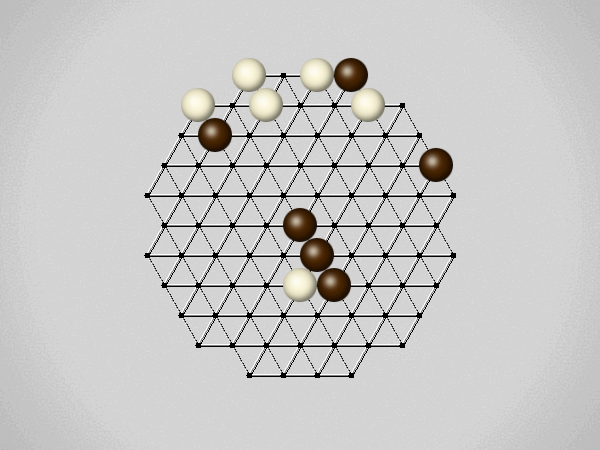
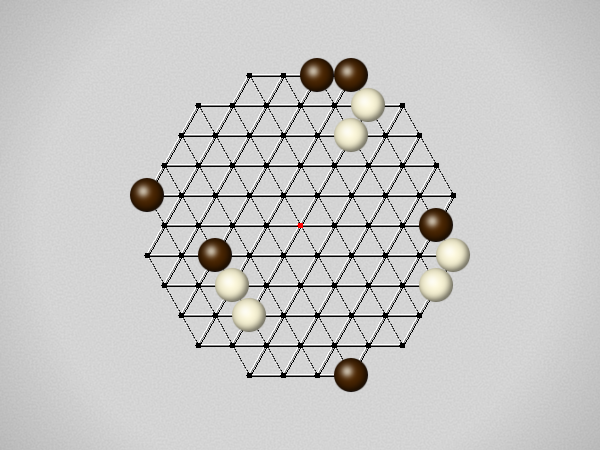
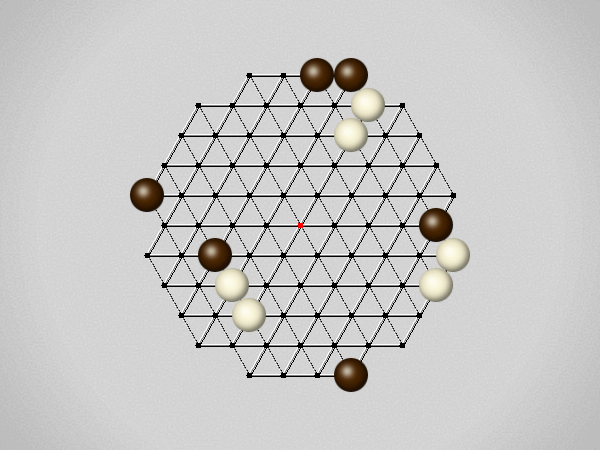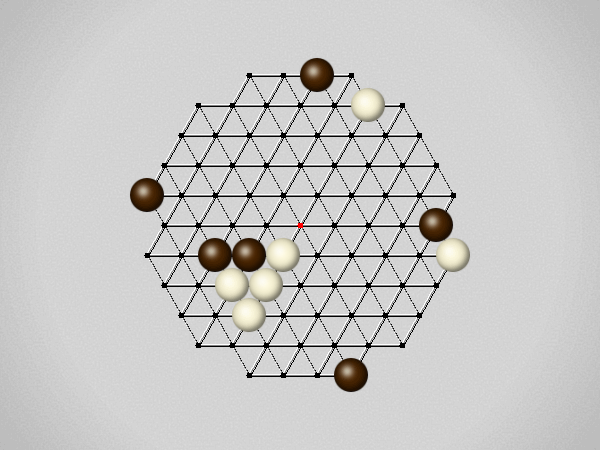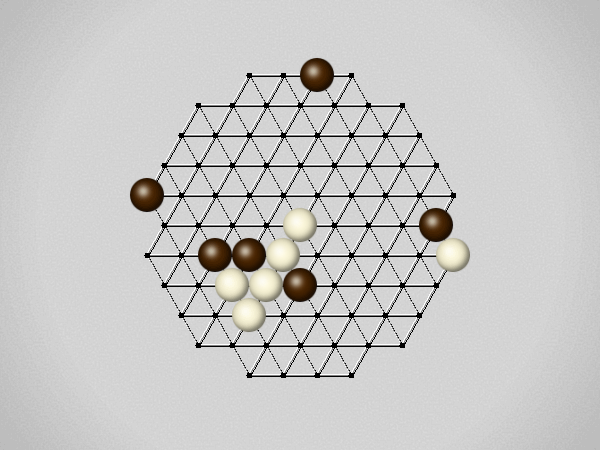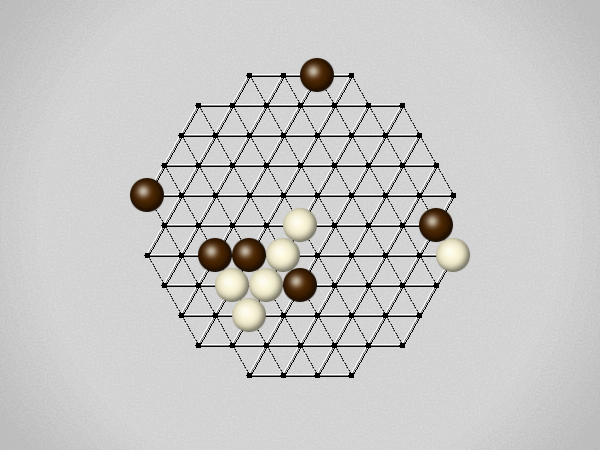
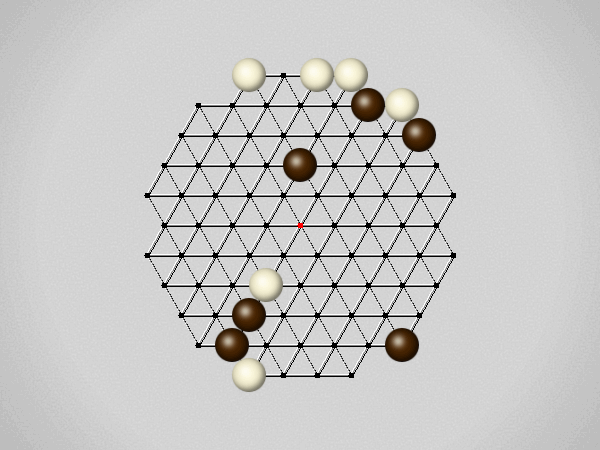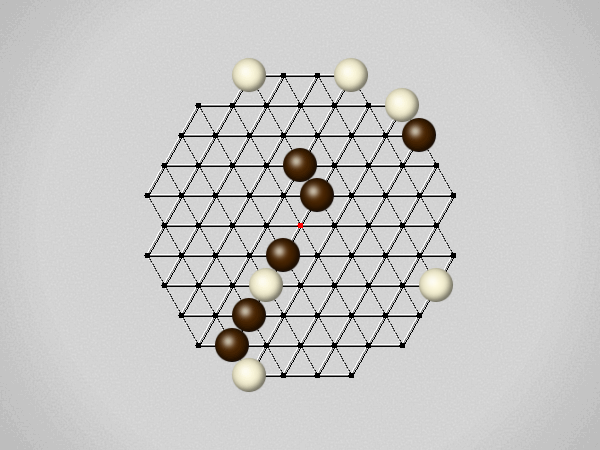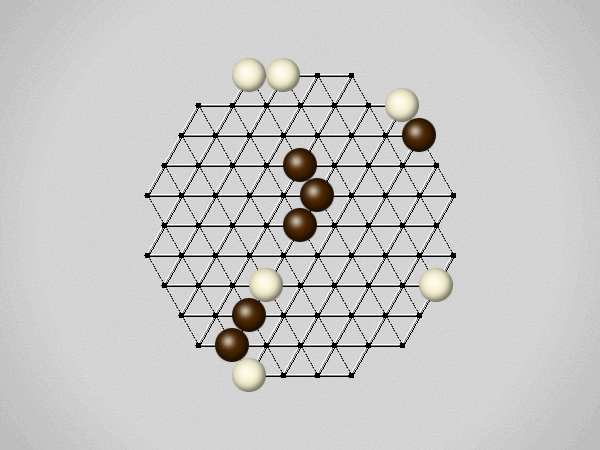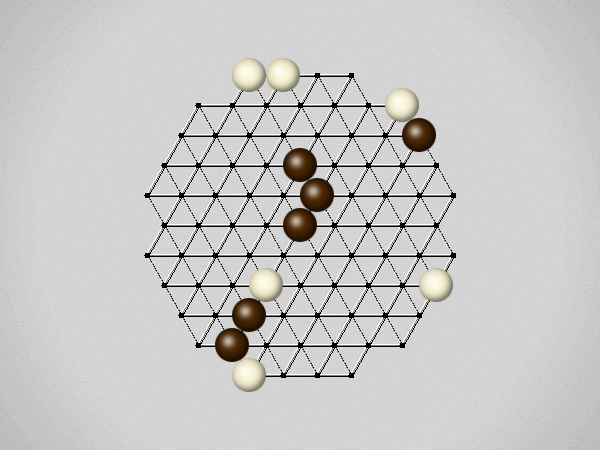
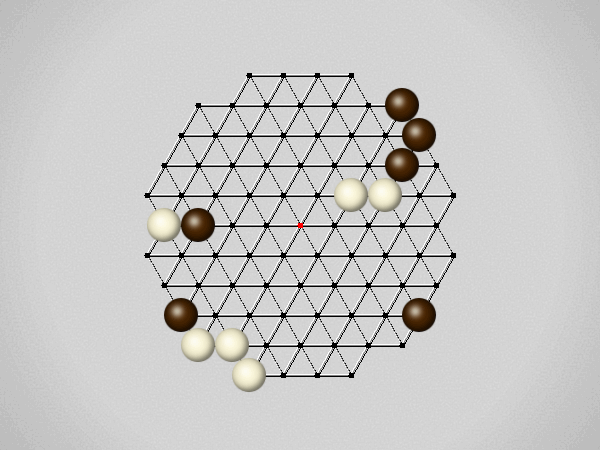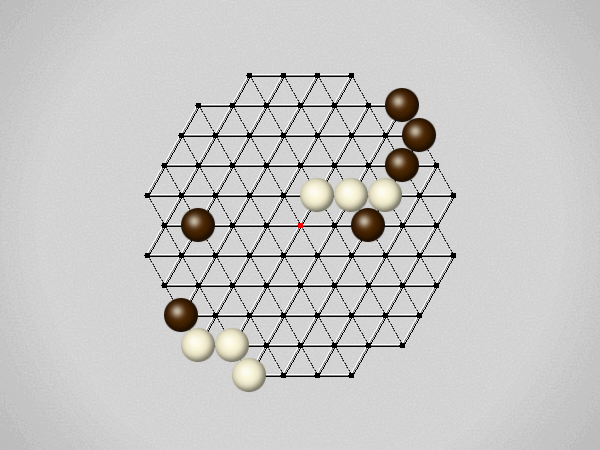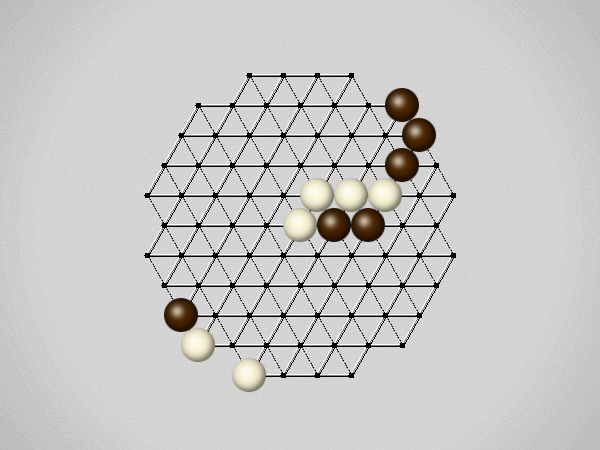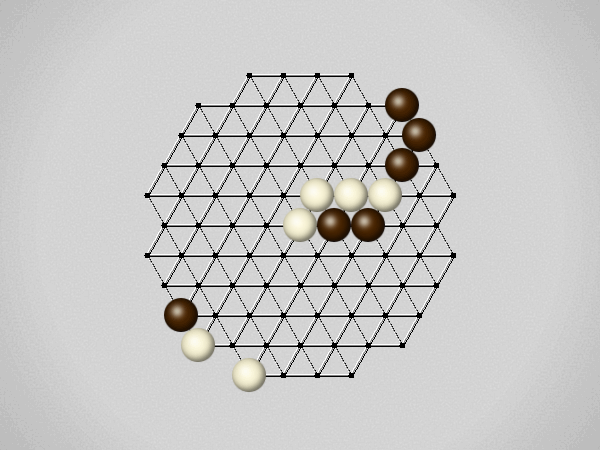
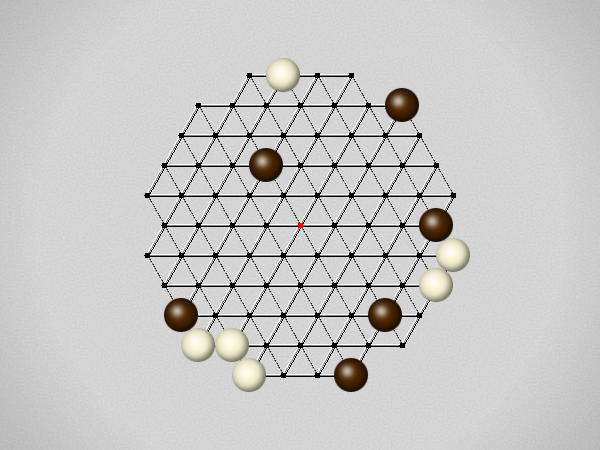
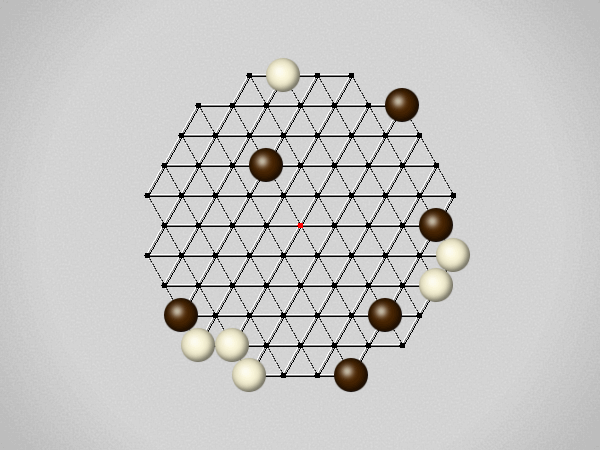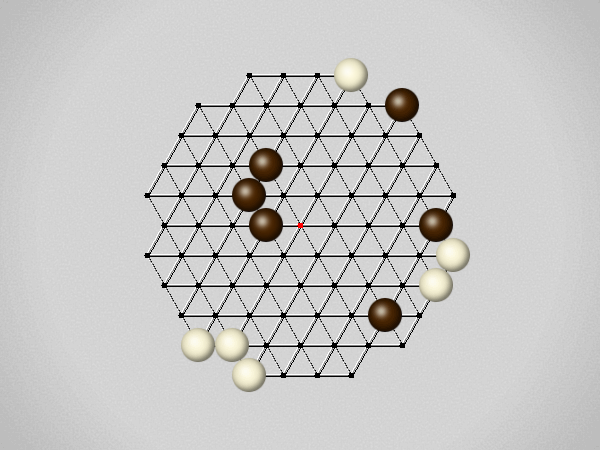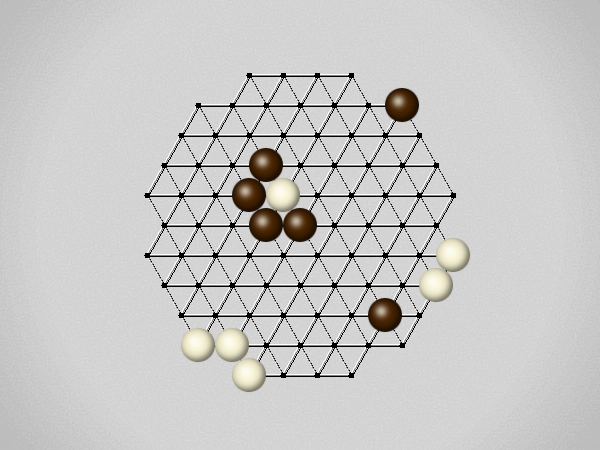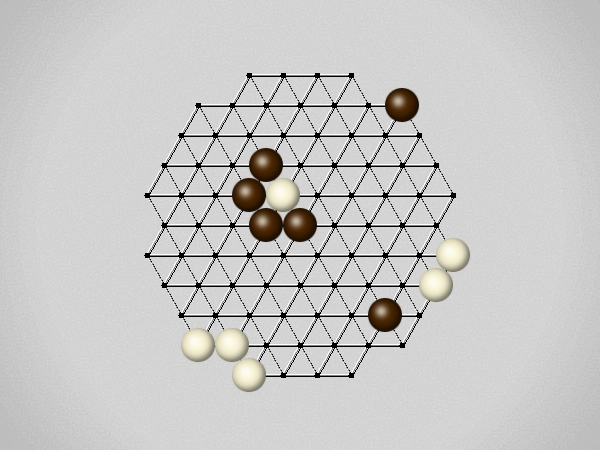
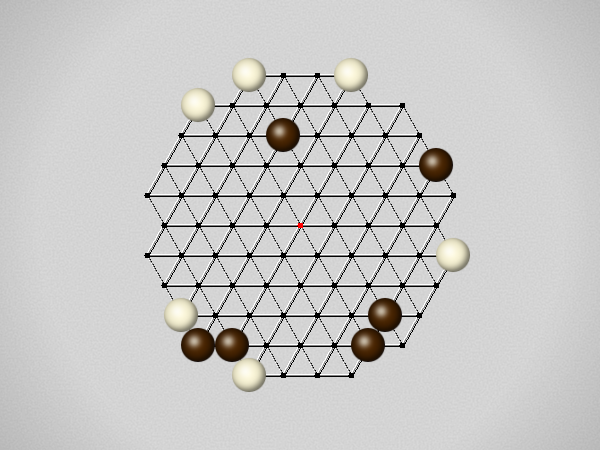
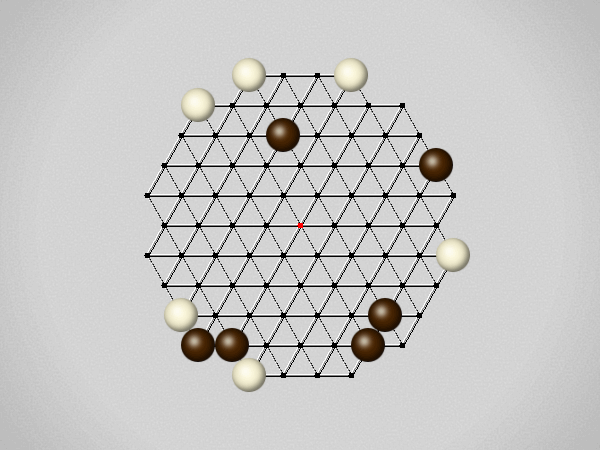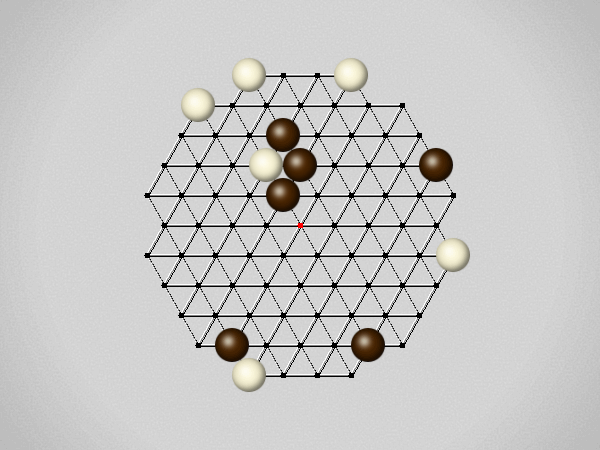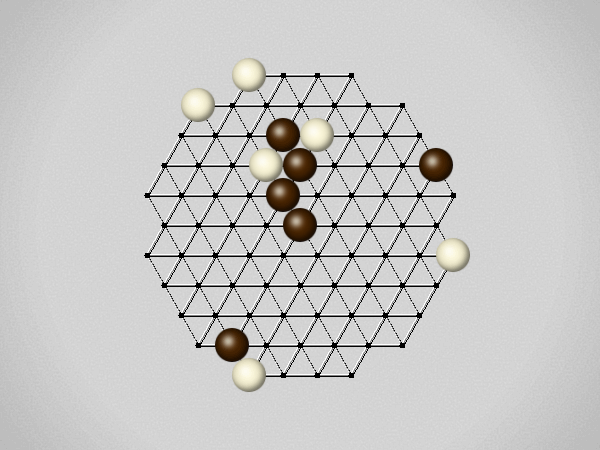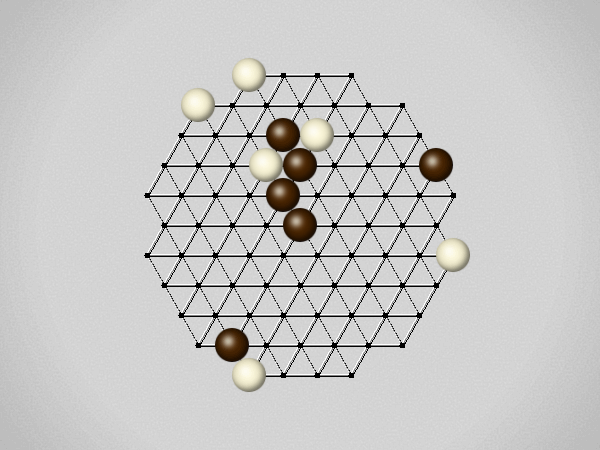
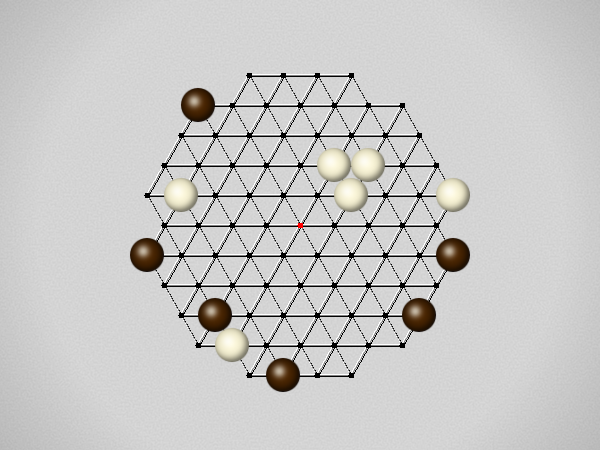
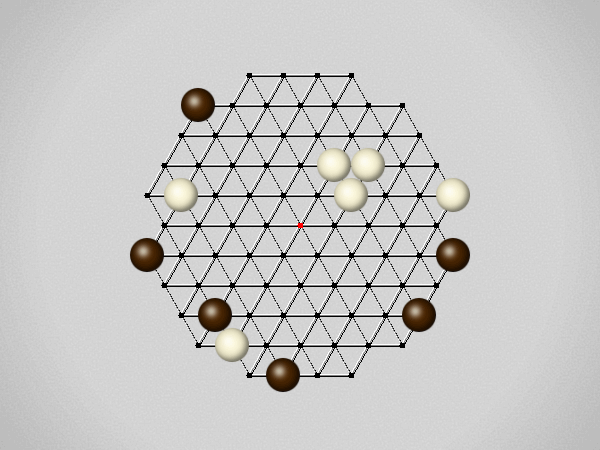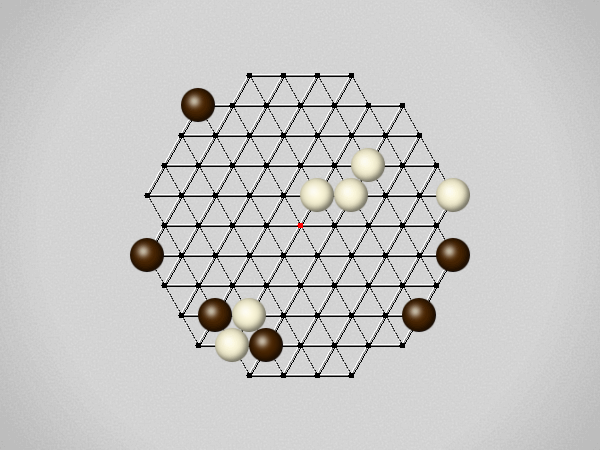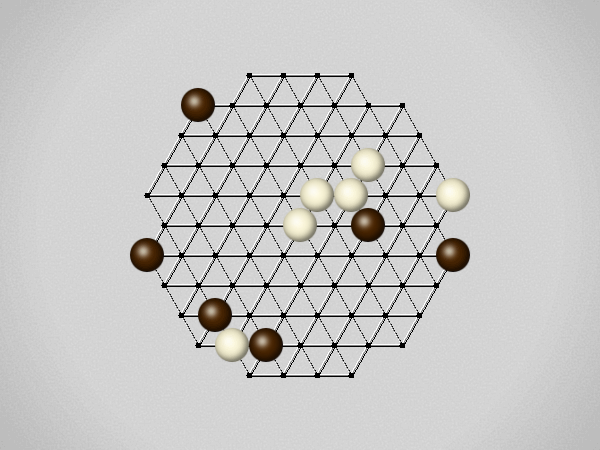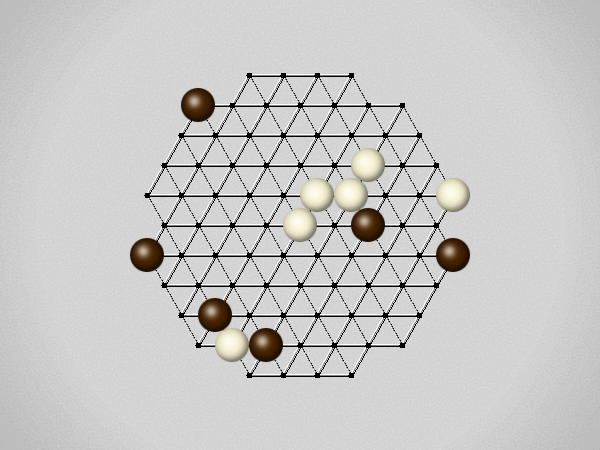
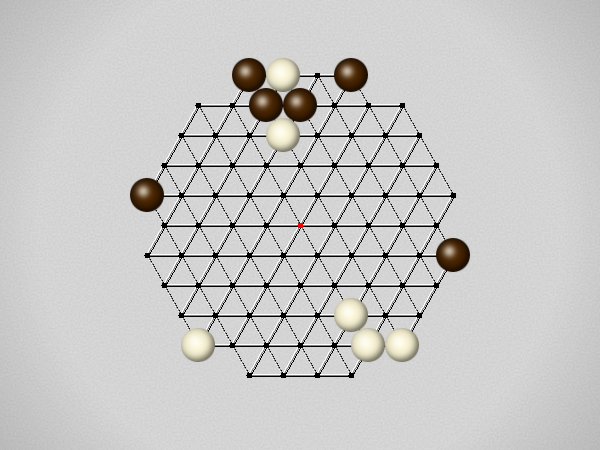
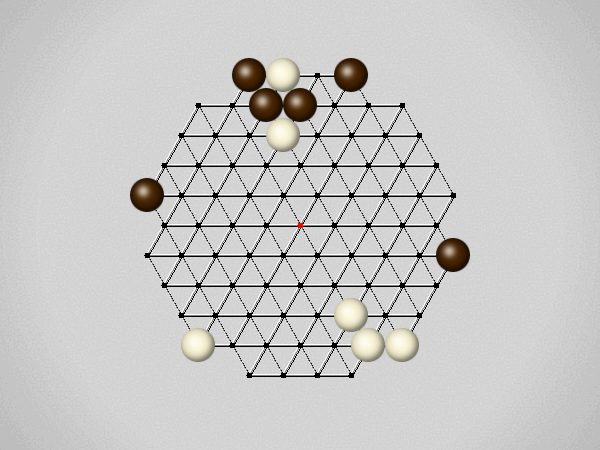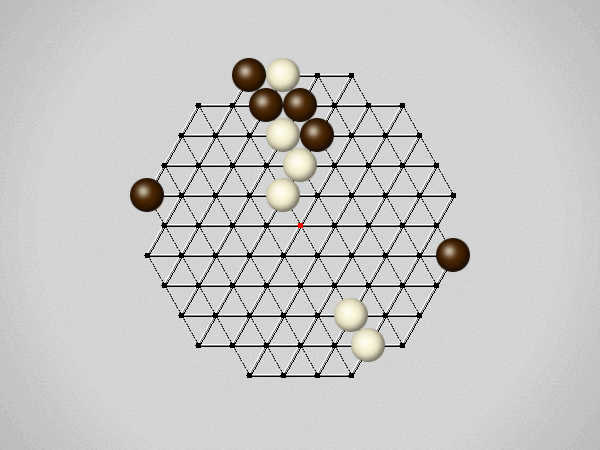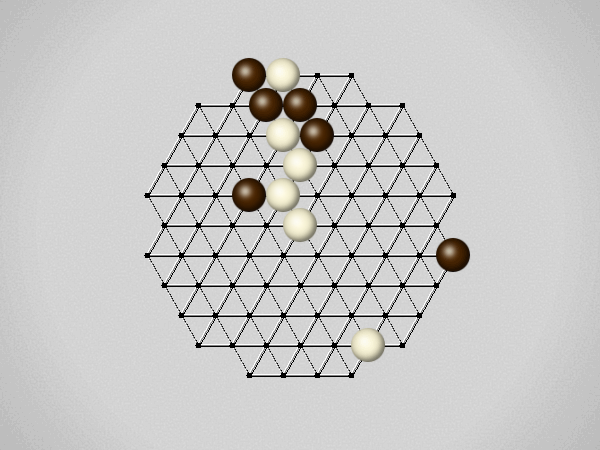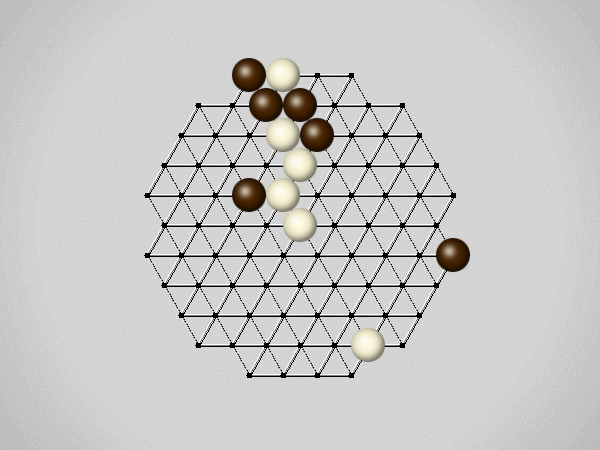
Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!
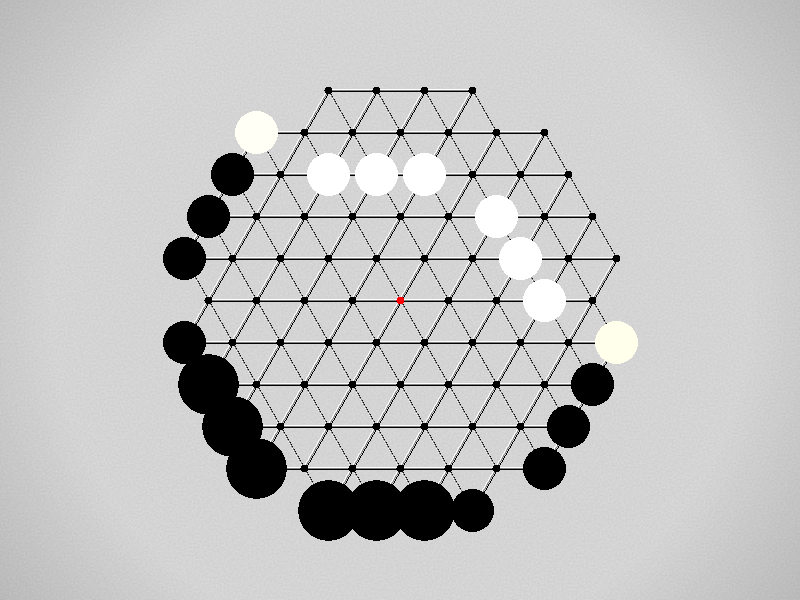
Goal
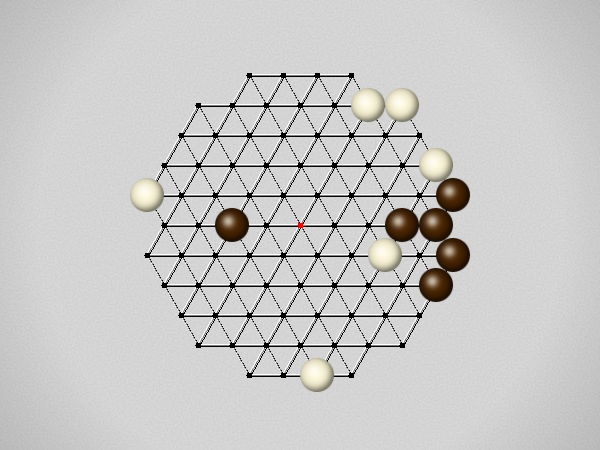
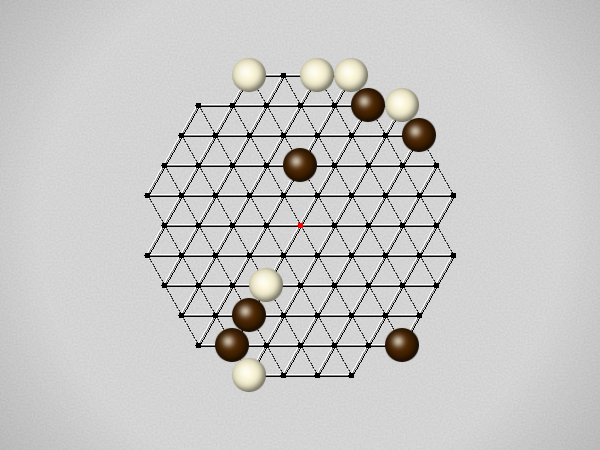
The first player to move a stone to the center wins!
Play
Each turn, move a stone along a line in a single direction as far as possible, stopping only at an edge or another stone.
Pie Rule
After the first player moves, the second player has the option to become the first player and take that move as his own.