Full Report for Star by Ea Ea

Rules

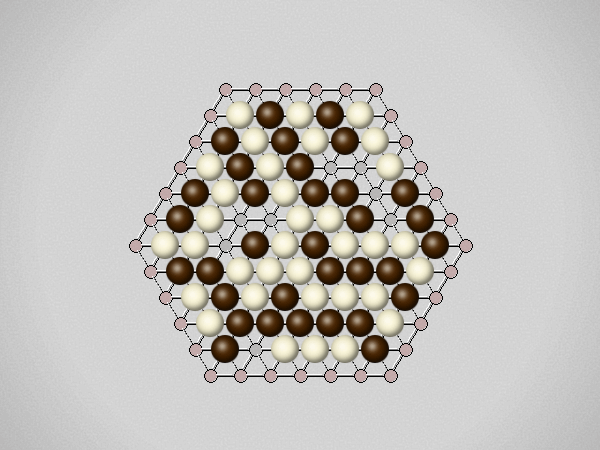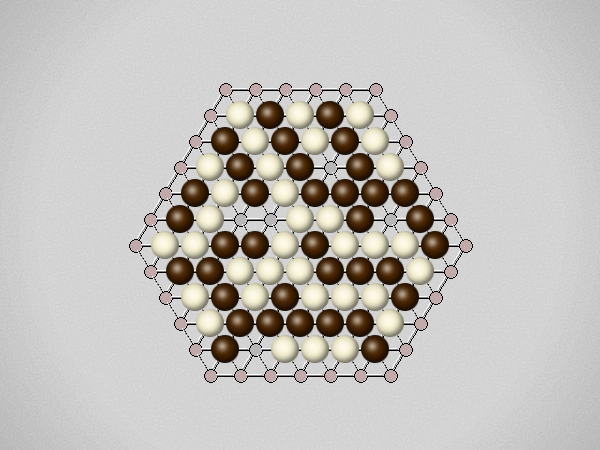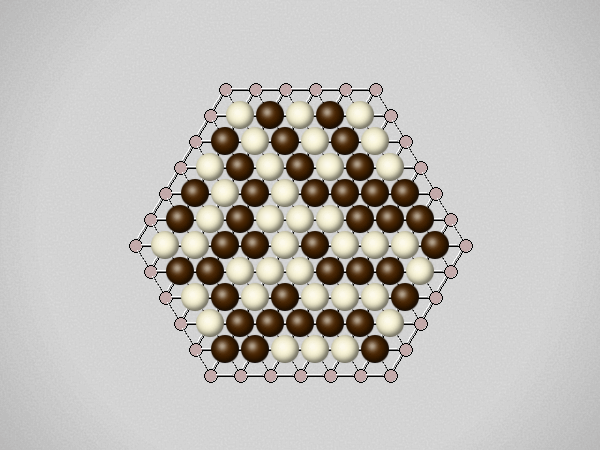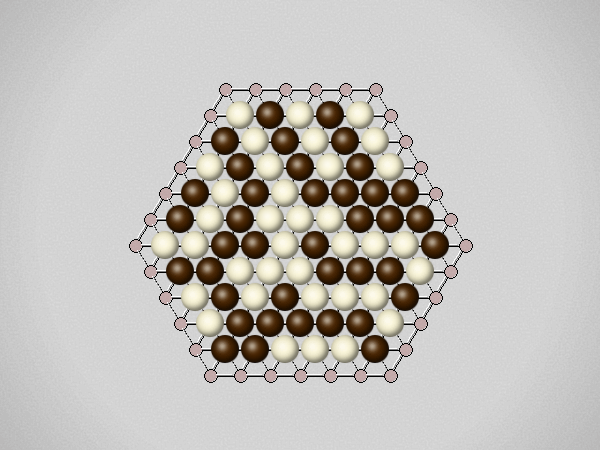
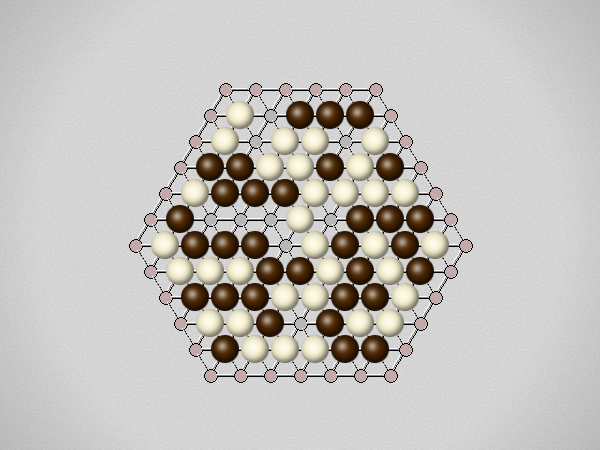
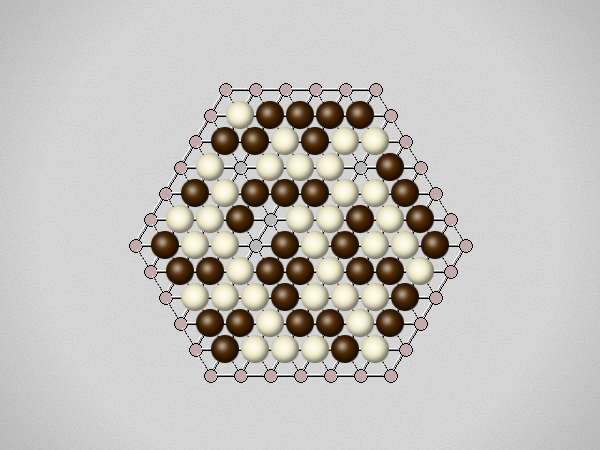
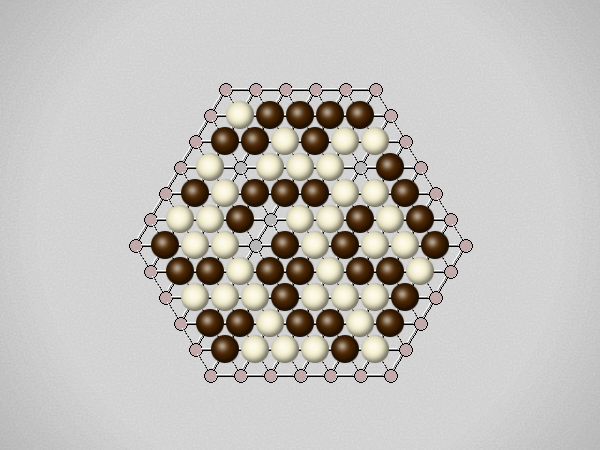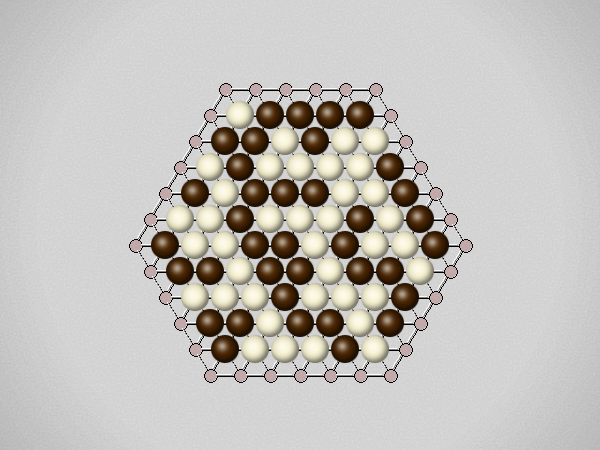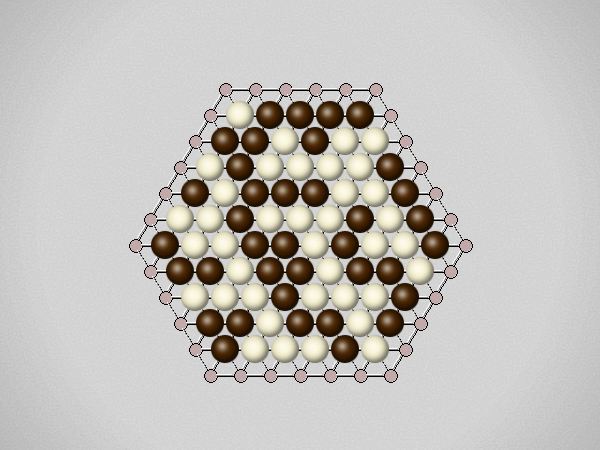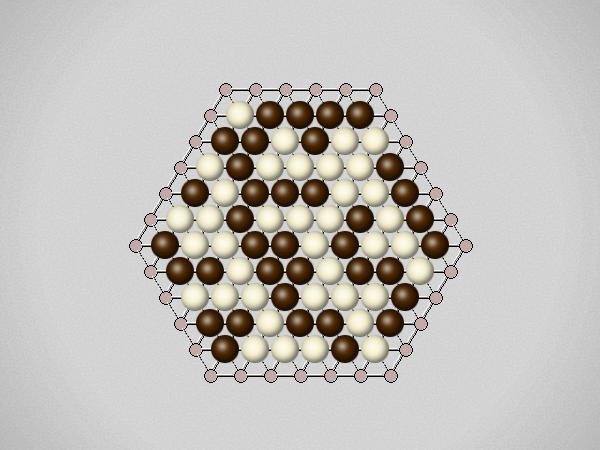
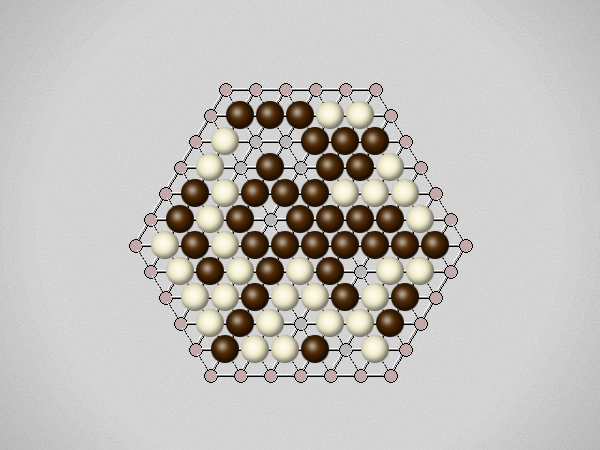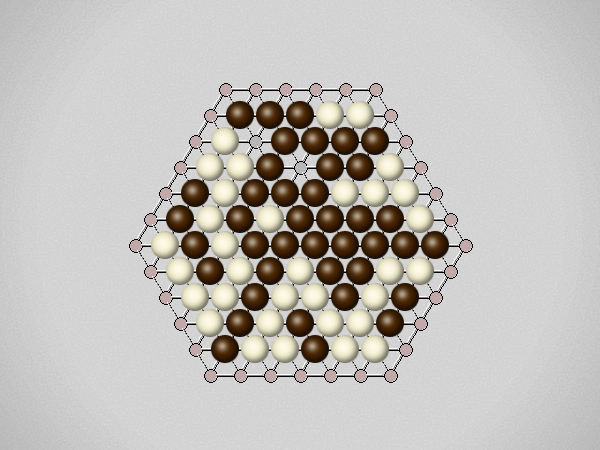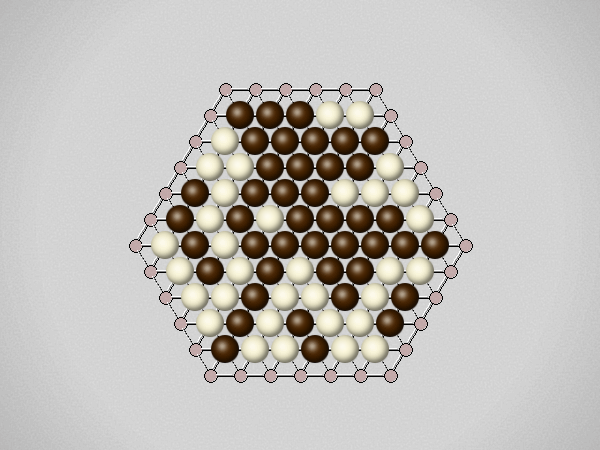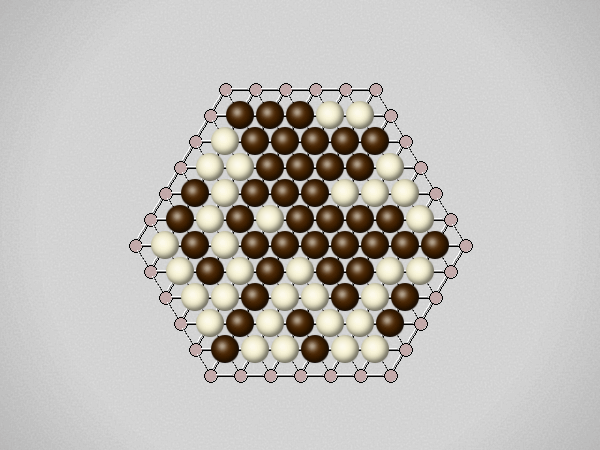
Representative game (in the sense of being of mean length). Wherever you see the 'representative game' referred to in later sections, this is it!

The game begins with one player placing a stone on the board. To avoid giving an advantage to the first player, a pie rule is used, allowing the second player to switch sides at that point. Players then alternate turns, placing a stone on an empty hexagon on the board. Players may pass; the game is over when both players pass.At the end of the game the players count their scores. A star is a group of connected stones belonging to one player that touches at least three partial edge hexagons. The score of a star is the number of edge hexagons it touches minus two. A player's score is the total of all the stars of that player's color. The player with the higher score wins.

Miscellaneous

General comments:

Play: Combinatorial

Mechanism(s): Connection,Scoring

BGG Stats

BGG Entry	Star
BGG Rating	6.66667
#Voters	3
SD	1.88562
BGG Weight	2
#Voters	1
Year	1983

BGG Ratings and Comments

User	Rating	Comment
bennetto	8
hiimjosh	4	Not particularly interesting. *Star looks quite a bit more entertaining though. Label: Disappointing
schwarzspecht	8

Kolomogorov Complexity Analysis

Size (bytes)	27086
Reference Size	10673
Ratio	2.54

Ai Ai calculates the size of the implementation, and compares it to the Ai Ai implementation of the simplest possible game (which just fills the board). Note that this estimate may include some graphics and heuristics code as well as the game logic. See the wikipedia entry for more details.

Playout Complexity Estimate

Playouts per second	94122.96 (10.62µs/playout)
Reference Size	562841.22 (1.78µs/playout)
Ratio (low is good)	5.98

Tavener complexity: the heat generated by playing every possible instance of a game with a perfectly efficient programme. Since this is not possible to calculate, Ai Ai calculates the number of random playouts per second and compares it to the fastest non-trivial Ai Ai game (Connect 4). This ratio gives a practical indication of how complex the game is. Combine this with the computational state space, and you can get an idea of how strong the default (MCTS-based) AI will be.

State Space Complexity

% new positions/bucket

State Space Complexity	75381911
State Space Complexity bounds	64143084 < 75381911 < ∞
State Space Complexity (log 10)	7.88
State Space Complexity bounds (log 10)	7.81 <= 7.88 <= ∞
Samples	863983
Confidence	0.00	0: totally unreliable, 100: perfect

State space complexity (where present) is an estimate of the number of distinct game tree reachable through actual play. Over a series of random games, Ai Ai checks each position to see if it is new, or a repeat of a previous position and keeps a total for each game. As the number of games increase, the quantity of new positions seen per game decreases. These games are then partitioned into a number of buckets, and if certain conditions are met, Ai Ai treats the number in each bucket as the start of a strictly decreasing geometric sequence and sums it to estimate the total state space. The accuracy is calculated as 1-[end bucket count]/[starting bucklet count]

Playout/Search Speed

Label	Its/s	SD	Nodes/s	SD	Game length	SD
Random playout	174,463	610	13,436,097	47,095	77	8
search.UCT	127,338	3,032			78	3

Random: 10 second warmup for the hotspot compiler. 100 trials of 1000ms each.

Other: 100 playouts, means calculated over the first 5 moves only to avoid distortion due to speedup at end of game.

Mirroring Strategies

Rotation (Half turn) lost each game as expected.
Reflection (X axis) lost each game as expected.
Reflection (Y axis) lost each game as expected.
Copy last move lost each game as expected.

Mirroring strategies attempt to copy the previous move. On first move, they will attempt to play in the centre. If neither of these are possible, they will pick a random move. Each entry represents a different form of copying; direct copy, reflection in either the X or Y axis, half-turn rotation.

Win % By Player (Bias)

1: White win %	33.33±21.28	Includes draws = 50%
2: Black win %	66.67±31.25	Includes draws = 50%
Draw %	0.00	Percentage of games where all players draw.
Decisive %	100.00	Percentage of games with a single winner.
Samples	9	Quantity of logged games played

Note: that win/loss statistics may vary depending on thinking time (horizon effect, etc.), bad heuristics, bugs, and other factors, so should be taken with a pinch of salt. (Given perfect play, any game of pure skill will always end in the same result.)

Note: Ai Ai differentiates between states where all players draw or win or lose; this is mostly to support cooperative games.

UCT Skill Chains

Match	AI	Strong Wins	Draws	Strong Losses	#Games	Strong Score	p1 Win%	Draw%	p2 Win%	Game Length
0	Random
2	UCT (its=3)	622	17	273	912	0.6606 <= 0.6913 <= 0.7205	51.21	1.86	46.93	76.89
6	UCT (its=7)	625	11	360	996	0.6026 <= 0.6330 <= 0.6624	51.81	1.10	47.09	77.61
12	UCT (its=13)	625	12	360	997	0.6025 <= 0.6329 <= 0.6623	49.45	1.20	49.35	77.40
20	UCT (its=21)	629	4	306	939	0.6413 <= 0.6720 <= 0.7013	50.27	0.43	49.31	77.52
29	UCT (its=30)	628	5	343	976	0.6155 <= 0.6460 <= 0.6754	53.79	0.51	45.70	77.29
38	UCT (its=39)	629	4	314	947	0.6357 <= 0.6663 <= 0.6956	49.42	0.42	50.16	77.43
49	UCT (its=50)	629	4	354	987	0.6089 <= 0.6393 <= 0.6687	51.87	0.41	47.72	77.53
64	UCT (its=65)	629	3	351	983	0.6109 <= 0.6414 <= 0.6708	52.19	0.31	47.51	77.63
75	UCT (its=204)	629	3	57	689	0.8919 <= 0.9151 <= 0.9337	49.64	0.44	49.93	76.86
76	UCT (its=554)	630	1	48	679	0.9067 <= 0.9286 <= 0.9456	51.69	0.15	48.16	77.38
77	UCT (its=1506)	630	1	49	680	0.9052 <= 0.9272 <= 0.9444	49.12	0.15	50.74	77.43
78	UCT (its=4095)	631	0	76	707	0.8675 <= 0.8925 <= 0.9133	43.71	0.00	56.29	77.97
79	UCT (its=11131)	268	0	44	312	0.8160 <= 0.8590 <= 0.8932	40.38	0.00	59.62	78.33
80	UCT (its=11131)	473	0	527	1000	0.4422 <= 0.4730 <= 0.5040	27.10	0.00	72.90	78.24

Search for levels ended: time limit reached.

Level of Play: Strong beats Weak 60% of the time (lower bound with 95% confidence).

Draw%, p1 win% and game length may give some indication of trends as AI strength increases.

1st Player Win Ratios by Playing Strength

This chart shows the win(green)/draw(black)/loss(red) percentages, as UCT play strength increases. Note that for most games, the top playing strength show here will be distinctly below human standard.

Complexity

Samples	9	Quantity of logged games played

Computational complexity (where present) is an estimate of the game tree reachable through actual play. For each game in turn, Ai Ai marks the positions reached in a hashtable, then counts the number of new moves added to the table. Once all moves are applied, it treats this sequence as a geometric progression and calculates the sum as n-> infinity.

Move Classification

Change in Material Per Turn

Board Size	null	Quantity of distinct board cells
Distinct actions	null	Quantity of distinct moves (e.g. "e4") regardless of position in game tree

Mean change in material/round	0.94	Complete round of play (all players)

This chart is based on a single representative* playout, and gives a feel for the change in material over the course of a game. (* Representative in the sense that it is close to the mean length.)

Actions/turn

Table: branching factor per turn, based on a single representative* game. (* Representative in the sense that it is close to the mean game length.)

Action Types per Turn

This chart is based on a single representative* game, and gives a feel for the types of moves available throughout that game. (* Representative in the sense that it is close to the mean game length.)

Red: removal, Black: move, Blue: Add, Grey: pass, Purple: swap sides, Brown: other.

Swap Heatmap (Full Scan)

Colour shows the frequency of swaps on turn 2 if this move is played on turn 1; black < red < yellow < white.

Based on 100 trials/move at 0.1s thinking time each.

Opening Heatmap

Colour shows the success ratio of this play over the first 10moves; black < red < yellow < white.

Size shows the frequency this move is played.

Swap Heatmap (Historic)

Colour shows the frequency of swaps on turn 2 if this move is played on turn 1; black < red < yellow < white.

Size shows the frequency this move is played.

Unique Positions Reachable at Depth

0	1	2	3	4
1	75	5700	213825	7709100

Note: most games do not take board rotation and reflection into consideration.
Multi-part turns could be treated as the same or different depth depending on the implementation.
Counts to depth N include all moves reachable at lower depths.
Inaccuracies may also exist due to hash collisions, but Ai Ai uses 64-bit hashes so these will be a very small fraction of a percentage point.

Shortest Game(s)

No solutions found to depth 4.

Puzzles

Puzzle	Solution
White to win in 16 moves
Black to win in 13 moves
White to win in 12 moves
Black to win in 6 moves
White to win in 12 moves
White to win in 14 moves
White to win in 12 moves

Weak puzzle selection criteria are in place; the first move may not be unique.